Сторінок 27, ілюстрацій 6, перелік посилань 3 джерела
Об'єкт роботи – ділення двох багаточленів.
Мета роботи – розробка програмного комплексу для ділення двох багаточленів, заданих користувачем
Програмний комплекс розроблений за допомогою середовища програмування Turbo Pascal 7.0. Він дозволяє для заданих коефіцієнтів двох багаточленів різних ступенів виконати операцію їх цілочисельного ділення з остатком.
Робота програмного комплексу успішно випробувана для кількох багаточленів з різними коефіцієнтами та старшими ступенями.
Робота рекомендована для практичного використання у якості швидкого та зручного засобу для виконання цілочисельного ділення з остатком двох багаточленів довільних ступенів.
ПРОГРАМНИЙ КОМПЛЕКС, БАГАТОЧЛЕН, ДІЛЕНННЯ, ДІЛИМЕ, ДІЛЬНИК, ОСТАТОК, ЦІЛОЧИСЕЛЬНЕ ДІЛЕННЯ, СТУПІНЬ
ЗМІСТ
| ВСТУП………………………………………………………………………… | |
| 1 ТЕОРЕТИЧНИЙ МАТЕРІАЛ…….………………………………………... | |
| 1.1 Алгебраїчні вирази……………………………………………………….. | |
| 1.2 Визначення многочлена………………………………………………….. | |
| 1.3 Дії над многочленами…………………………………………………….. | |
| 1.4 Розкладення багаточленів на множники………………………………… | |
| 1.5 Возвратні рівняння………………………………………………………... | |
| 1.6 Використання многочленів для інтерполяції…………………………… | |
| 2 ОПИС АЛГОРИТМУ…………………..……………………....................... | |
| 2.1 Алгоритм програми………………………………………………………. | |
| 3 ПРОГРАМНА РЕАЛІЗАЦІЯ АЛГОРИТМУ……………………………... | |
| 3.1 Блок-схема………………………………………………………………… | |
| 3.2 Мінімальні системні вимоги…………………………………………….. | |
| 3.3 Інтерфейс користувача…………………………………………………… | |
| 4 ПРИКЛАД РОБОТИ ПРОГРАМНОГО КОМПЛЕКСУ…………………. | |
| ВИСНОВКИ…………………………………………………………………… | |
| ПЕРЕЛІК ПОСИЛАНЬ……………………………………………………….. | |
| РЕЗЮМЕ………………………………………………………………………. | |
| ДОДАТОК А. ЛІСТИНГ ПРОГРАМИ……………………………………… |
ВСТУП
У неозорому царстві функцій многочлени займають, на перший погляд, дуже скромне місце. Проте це перше враження брехливе.
Многочлени, дійсно, гранично прості: запис алгебри
| f(x) = xn + a1xn–1 + a2xn–2 +... + an–1x + an | ( |
є одночасно і формулою для обчислення значень многочлена. Хоча вирази типу cosx, 5√x, 10x, log2x набагато лаконичнее, з обчислювальної точки зору вони беззмістовні: для обчислення, скажемо чисел cos17°, 5√2, 100,13 чи log27 потрібні спеціальні наближені формули (або таблиці, складені за допомогою тих же формул). Як правило, в таких формулах з'являються многочлени.
Адже тригонометричні, статечні і тому подібне (елементарні) функції — це найпростіші з функцій аналізу, що вивчаються і використовуваних математиками, фізиками, інженерами. Відомий математик-обчислювач Р.В.Хеммінг в своїй книзі «Чисельні методи» (М., «Наука», 1972) пише: «Оскільки з многочленами легко звертатися, велика частина класичного чисельного аналізу грунтується на наближенні многочленами».
Оскільки обчислювати многочлени доводиться часто, то важливо навчитися робити це якомога простіше. Ми розповімо про еволюцію методів обчислення значень многочленів з моменту зародження (XVIIст) та про один з методів виконання цілочисельного ділення многочленів.
Метою даної роботи є створення програмного комплексу для виконання цілочисельного ділення з остатком двох багаточленів, які задаються користувачем у вигляді коефіцієнтів при відповідних ступенях змінної.
1 ТЕОРЕТИЧНИЙ МАТЕРІАЛ
1.1 Алгебраїчні вирази
Вирази алгебри розділяються на раціональних і ірраціональних.
Вираз алгебри називається раціональним щодо змінної величини, що входить в цей вираз, якщо над цією величиною проводяться дії складання, віднімання, множення, ділення, зведення в цілу ступінь.
Приклади раціональних величин.

Вираз алгебри називається ірраціональним щодо змінної величини, що входить в цей вираз, якщо воно містить величину під знаком кореня.
Приклади ірраціональних величин.

Раціональні вирази бувають цілі і дроби
Цілий раціональний вираз по-іншому називається многочленом (поліномом). Многочленом називається раціональний вираз, в якому над змінній величиною проводяться тільки дії складання, віднімання і множення.
Приклади многочленів.

Многочлен n – й ступені відносно х
 (1.1)
(1.1)
Многочленом нульового ступеня є не будь-яке рівне нулю число. Число нуль також многочлен тільки невизначеному ступеню. Кожен член многочлена називається одночленом. Ступінь змінної або сума ступенів змінних що входять в одночлен називається ступенем одночлена.
Приклад одночлена
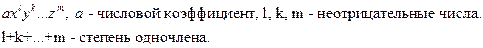 (1.2)
(1.2)
Одночлен – окремий випадок многочлена. Найбільша із ступенів одночленів що входять в многочлен ступенем многочлена. Інше визначення многочлена: многочлен – сума одночленів.
Многочлен вигляду
 (1.3)
(1.3)
- многочлен від однієї змінної.
Многочлен в склад, якого входять одночлени вигляду
 (1.4)
(1.4)
Дробовим раціональним виразом або дробом алгебри називається відношення двох многочленів.
Приклад дробу алгебри

1.2 Визначення многочлена
У математиці, многочлени або поліноми від однієї змінної, це вирази вигляду
 (1.5)
(1.5)
де ci фіксовані коефіцієнти, а x — змінна. Многочлени складають один з найважливіших класів елементарних функцій.
Вивчення поліноміальних рівнянь і їх рішень складало чи не головний об'єкт «класичної алгебри». З вивченням многочленів пов'язаний цілий ряд перетворень в математиці: введення в розгляд нуля, негативних, а потім і комплексних чисел, а також поява теорії груп як розділу математики і виділення класів спеціальних функцій в аналізі.
Технічна простота обчислень, пов'язаних з многочленами, в порівнянні з складнішими класами функцій, а також той факт, що безліч многочленів щільна в просторі безперервних функцій на компакных підмножинах евклідова простори (дивися теорема апроксимації Вейерштраса), сприяли розвитку методів розкладання в ряди і поліноміальної інтерполяції в математичному аналізі.
Многочлени також грають ключову роль в геометрії алгебри, об'єктом якої є множини, визначені як вирішення систем многочленів. Особливі властивості перетворення коефіцієнтів при множенні многочленів використовуються в геометрії алгебри, алгебрі, теорії вузлів і інших розділах математики для кодування, або виразу многочленами властивостей різних об'єктів.
Коефіцієнти многочлена зазвичай беруться з певного комутативного кільця R (частіше за все поле, наприклад, поля дійсних або комплексних чисел). В цьому випадку, щодо операцій складання і множення многочлени утворюють кільце (більш того асоціативно-комутативну алгебру над кільцем R без дільників нуля) яке позначається:
 (1.6)
(1.6)
Многочлен вигляду  називається одночленом або мономом
називається одночленом або мономом
Одночлен, відповідний мультииндексу  називається вільним членом.
називається вільним членом.
У разі, коли многочлен має всього два ненульові члени, його називають двочленом або біномом
У разі, коли многочлен має всього три ненульові члени, його називають тричленом.
Повним ступенем (ненульового) одночлена  називається ціле число
називається ціле число  .
.
Ступенем многочлена називається максимальна із ступенів його одночленів, тотожний нуль не має ступеня
Безліч мультииндексов I для яких коефіцієнти cI ненульові називається носієм многочлена, а його опукла оболонка многогранником Ньютона.
Многочлен, який можна представити у вигляді твору многочленів нижчих ступенів з коефіцієнтами з даного поля, називається таким, що приводиться (над даним полемо), інакше — що не приводиться. Многочлени, що не приводяться, грають в кільці многочленів роль, схожу з роллю простих чисел в кільці цілих чисел. Наприклад, вірна теорема: якщо твір pq ділиться на многочлен л, що не приводиться, то p або q ділиться на л. Кожен многочлен, ступені більшої нуля, розкладається в даному полі в твір множників, що не приводяться, єдиним чином (з точністю до множників нульового ступеня).
Наприклад, многочлен x4 + 2, що не приводиться в полі раціональних чисел, розкладається на два множники в полі дійсних чисел і на чотири множники в полі комплексних чисел.
Взагалі, кожен многочлен від одного змінного x розкладається в полі дійсних чисел на множники першого і другого ступеня, в полі комплексних чисел — на множники першого ступеня (основна теорема алгебри).
Для двох і більшого числа змінних цього вже не можна затверджувати. Над будь-яким полем для будь-якого n > 2 існують многочлен від n змінних, що не приводяться в будь-якому розширенні цього поля. Такі многочлени називаються такими, що абсолютно не приводяться.
Властивості многочленів
Кільце многочленів над довільною областю цілісності само є областю цілісності.
Кільце многочленів від будь-якого кінцевого числа змінних над будь-яким факторіальним кільцем само є факторіальним.
Кільце многочленів від одного змінного над полем є кільцем головних ідеалів, тобто будь-який його ідеал може бути породжений одним елементом.
Більш того, кільце многочленів від одного змінного над полем є евклидовым кільцем.
1.3 Дії над многочленами
Визначення. Два многочлени P(x) і Q(x) відносно х з будь-якими дійсними коефіцієнтами рахуватимемо рівними P(x)= Q(x) лише в тому випадку, якщо рівні їх коефіцієнти при однакових ступенях х.
Значення таких многочленів очевидно рівні. Існує твердження зворотне цьому: якщо значення двох многочленів рівні при всіх значеннях х, то такі многочлени рівні, їх коефіцієнти співпадають при однакових ступенях х.
Многочлени можна складати. Сумою двох многочленів P(x) і Q(x) називається многочлен, у якого коефіцієнт при кожному ступені х рівний сумі коефіцієнтів при тому ж ступені в многочленах P(x) і Q(x).
Многочлени можна віднімати. Різницею двох многочленів P(x) і Q(x) називається многочлен, у якого коефіцієнт при кожному ступені х рівний різниці коефіцієнтів при тому ж ступені в многочленах P(x) і Q(x).
Многочлени можна умножати. Щоб помножити два многочлени P(x) і Q(x), потрібно кожен член многочлена P(x) помножити на кожен член многочлена Q(x) і отримані результати скласти.
Складання, множення і віднімання многочленів – основні арифметичні дії над многочленами.
Хай P(x)= Q(x)S(x), P(x) і Q(x) два многочлени, причому ступінь многочлена P(x) не менше ступеня многочлена Q(x) і, якщо існує такий многочлен S(x), що виконується рівність
P(x)= Q(x)S(x), то говорять, що многочлен P(x) ділиться без остачі на многочлен Q(x). P(x), Q(x), S(x) називаються відповідно ділиме, дільник, приватне. Якщо такого многочлена не існує, то многочлен P(x) не ділиться на Q(x). В цьому випадку, як і при розгляді ділення з числами проводиться ділення із залишком.
Розділити многочлен P(x) на Q(x) із залишком це означає представити многочлен P(x) у вигляді рівності P(x)= Q(x)S(x)+ R(x), де R(x) залишок, причому ступінь R(x) менше ступеня Q(x).При діленні многочленів із залишком справедлива наступна теорема.
Для будь-яких двох многочленів P(x) і Q(x) завжди можна знайти і притому однозначний два многочлени S(x) і R(x), для яких справедлива рівність P(x)= Q(x)S(x)+ R(x).
Ділення двох многочленів здійснюється кутом. Розглянемо приклад такого ділення.
Приклад 1. Виконати ділення P(x)= x3 – 1 на Q(x)= x + 1. Виконаємо ділення кутом.

Звідси отримуємо x3 – 1 = (x + 1)(x2 – x + 1) – 2. Приватне S(x)= x2 – x + 1, залишок R(x)= - 2.
Приклад 2. Виконати ділення P(x)= x4 +4x3 – 4x2 + x + 1 на Q(x)= x2 +2x + 1. Виконаємо ділення кутом.

Звідси отримуємо: x4 + 4x3 – 4x2 + x + 1 = (x2 +2x + 1)(x2 + 2x – 9) +17 x + 10.
Можна знайти приватне від ділення двох многочленів методом невизначених коефіцієнтів
x4 +4x3 – 4x2 + x + 1 = (x2 +2x + 1)(ax2 + bx + c) + dx + e
x4 +4x3 – 4x2 + x + 1 = ax4 +(2a + b)x3 +(c + 2b + a)x2 +(b + d + 2c)x + e + c
Прирівнюємо коефіцієнти при однакових ступенях

Отримуємо той же результат.
x4 + 4x3 – 4x2 + x + 1 = (x2 +2x + 1)(x2 + 2x – 9) +17 x + 10
Коефіцієнти приватного многочлена на двочлен можна шукати з використанням визначення рівності двох многочленів.
Хай
P(x) = a 0xn + a 1xn-1 +…+ a n-1x + a n; Q(x) = x – с; S(x) = b 0xn-1 + b 1xn-2 +…+ b n-1.
Отримуємо
a 0xn + a 1xn-1 + … + a n-1x + a n = (x – с)(b 0xn-1 + b 1xn-2 + … + b n-1) + R (1.7)
де R – число оскільки ступінь R менше ступеня x – з. Помножимо S(x) на Q(x) і отримаємо
a 0xn + a 1xn-1 + … + a n-1x + a n = b 0xn + (b 1 - c b 0 )xn-1 + … +(bn -1 - c bn -2 )x + R - c bn -1 (1.8)
Звідси отримаємо
b 0 = a 0; bk = cbk-1 + ak (k = 1, 2, 3,…, n), bn = R. R= сbn-1 + an (1.9)
Таким чином, ділення на двочлен можна здійснювати, не проводячи «ділення кутом», а визначати коефіцієнти приватного по отриманих формулах. Подібний спосіб визначення коефіцієнтів називається схемою Горнера.
1.4 Розкладення багаточленів на множники
Теорему Безу використовують для розкладання многочлена на множники.
Визначення.Перетворення многочлена до виду твору два або декількох многочленів ненульового ступеня називається розкладанням многочлена на множники. Якщо многочлен може бути розкладений на множники, то він називається таким, що приводиться, інакше – що не приводиться або нерозкладним на множники.
Многочлен
P(x) = a 0xn + a 1xn-1 + … + a n-1x + a n (1.10)
приводимо на безлічі комплексних чисел, але не завжди приводиться на безлічі дійсних або раціональних чисел. Можна розглянути такий приклад. Многочлен P(x) = x2 + 9 не приводимо на безлічі дійсних чисел, а на множині комплексних ми отримаємо наступне розкладання x2 + 9 = (x + 3i)(x – 3i). Де i =  - мнима одиниця. Многочлен P(x) можна представити у вигляді
- мнима одиниця. Многочлен P(x) можна представити у вигляді
P(x) = a 0(x – x1)(x – x2)…(x – xn). (1.11)
Якщо провести множення двочленів і привести подібні, складаючи коефіцієнти при однакових ступенях, то отримаємо многочлен вигляду:
a 0xn + a 1xn-1 + … + a n-1x + a n = a 0(xn – (x1 + x2 + …+ xn)xn-1 + (1.12)
(x1x2 + …+ xn-1 xn) xn-2 + … +(-1)n x1x2…xn).
За визначенням рівних многочленів порівняємо коефіцієнти при однакових ступенях многочленів.
 (1.13)
(1.13)
Ці формули носять назву формул Вієта. Формули дозволяють по відомому корінню скласти рівняння, яке можна записати у вигляді
 (1.14)
(1.14)
Для розкладання многочленів на множники корисно знати ще дві теореми.
Теорема про число коріння многочлена і розкладання його на лінійні множники. Всякий многочлен, що розглядається на безлічі комплексних чисел, має рівно стільки коріння, який його ступінь, і завжди розкладається на лінійні множники вигляду:
a 0xn + a 1xn-1 + … + a n-1x + a n = a 0(x – x1)(x – x2)…(x – xn). (1.15)
Теорема про розкладання на множники з дійсними коефіцієнтами. Многочлен з дійсними коефіцієнтами завжди розкладається в твір лінійних і квадратичних множників, коефіцієнти яких також дійсні.
На підставі попередніх тверджень можна зробити такий вивід, що раціональне коріння рівняння з цілими коефіцієнтами слід шукати серед чисел вигляду  де p і q – всілякі дільники (як позитивні, так і негативні!) відповідно вільного члена рівняння і коефіцієнта при старшому ступені. При знаходженні одного кореня ми можемо за допомогою схеми Горнера знизити ступінь многочлена на одиницю.
де p і q – всілякі дільники (як позитивні, так і негативні!) відповідно вільного члена рівняння і коефіцієнта при старшому ступені. При знаходженні одного кореня ми можемо за допомогою схеми Горнера знизити ступінь многочлена на одиницю.
1.5 Возвратні рівняння
Рівняння четвертого ступеня ax4 + bx3 + cx2 + dx + e = 0 называють возвратним, якщо при b ¹ 0 и a ¹ 0 рівняння задовольняє умові
 (1.16)
(1.16)
Для рішення поділимо на x2 ¹ 0, отримаємо рівняння виду:


Отримаємо рівняння
 (1.17)
(1.17)
1.6 Використання многочленів для інтерполяції
Мета завдання про наближення (інтерполяції): дану функцію у(х) потрібно приблизно замінити деякою функцією j(х), властивості якої нам відомі так, щоб відхилення в заданій області було найменшим. інтерполяційні формули застосовуються, перш за все, при заміні графічно заданій функції аналітичною, а також для інтерполяції в таблицях.
Методи інтерполяції Лагранжа і Ньютона
Один з підходів до завдання інтерполяції — метод Лагранжа. Основна ідея цього методу полягає в тому, щоб перш за все знайти многочлен, який приймає значення 1 в одній вузловій точці і 0 у всіх інших. Легко бачити, сто функція є необхідним многочленом ступеня n; він рівний 1, если x=xj и 0, когда x=xi, i¹j. Многочлен Lj(x)×yj приймає значення yi в i-й вузловій точці і рівний 0 у всіх інших вузлах. З цього виходить, що є многочлен ступеня n, що проходить через n+1 крапку (xi, yi).
Інший підхід — метод Ньютона (метод розділених різниць). Цей метод дозволяє набути апроксимуючих значень функції без побудови в явному вигляді апроксимуючого полінома. В результаті отримуємо формулу для полінома Pn, що апроксимує функцію f(x):
P(x)=P(x0)+(x-x0)P(x0,x1)+(x-x0)(x-x1)P(x0,x1,x2)+…+ (1.18)
(x-x0)(x-x1)…(x-xn)P(x0,x1,…,xn);
— розділена різниця 1-го порядку;
— розділена різниця 2-го порядку і так далі
Значення Pn(x) у вузлах співпадають із значеннями f(x).
Фактично формули Лагранжа і Ньютона породжують один і той же поліном, різниця тільки в алгоритмі його побудови.
2 ОПИС АЛГОРИТМУ
2.1 Алгоритм програми
Алгоритмом програми є правило «ділення в стовпчик» багаточленів, при якому, на відміну від звичайного ділення чисел, береться до уваги також ступені одночленів, що входять до складу багаточлена.
Представимо короткий опис алгоритму у вигляді послідовності пунктів:
1) ввід двох багаточленів, другий з яких має ступінь менше чи рівну ступені першого багаточлена;
2) ділимо перший член діли мого на перший член дільника, отриманий результат є першим членом результату;
3) умножаємо отриманий член на дільник, результат множення записуємо під ділимим, подібний член під подібним;
4) віднімаємо члени результату з відповідних членів ділимого, зносимо слідуючий по порядку член діли мого;
5) перший член остатку ділимо на перший член дільника, результат є другим членом результату;
6) таким чином продовжуємо кроки 1)-4) доки ступінь остатку не стане меншою за ступінь дільника, або на очередному кроці цілочисельне ділення буде неможливим, оскільки коефіцієнт ділимого буде менше за відповідний коефіцієнт дільника.
Наприкінці виконання алгоритму отримуємо два багаточлени – результат ділення та остаток від ділення.
3 ПРОГРАМНА РЕАЛІЗАЦІЯ АЛГОРИТМУ
3.1 Блок-схема

Рис. 3.1 – Блок-схема програми
3.2 Мінімальні системні вимоги
Для коректної роботи програма потребує наступні мінімальні системні вимоги:
а) Windows 98;
б) процесор 33 МГц;
в) 3 Кб вільного місця на жорсткому диску;
г) 2 Мб вільної оперативної пам’яті.
3.3 Інтерфейс користувача
Програму рекомендується запускати з командної строки. Запуск виконується командою «mnogochl.exe».
Вікно програми при запуску показане на рис. 3.2.

Рис. 3.2 - Початковий стан вікна програми
Одразу ж після запуску програма запитує у користувача старшу ступінь першого багаточлена. Необхідно просто ввести ціле число над курсором, яке є ступінню першого багаточлена.
Після цього програма запросить ввести коефіцієнти багаточлена з вказаним ступенем. Слід замітити, що кількість коефіцієнтів дорівнює ступені +1, оскільки рахується також вільний член при нульовому ступені змінної.
Користувач вводить коефіцієнти, а програма після натиснення клавіші Enter автоматично перетворює багаточлен, що ввів користувач, у стандартний для сприйняття вигляд – записує його через ступені змінної, починаючи з найстаршої. Вікно програми показане на рис. 3.3.

Рис. 3.3. – Перетворення багаточлена до стандартного вигляду
Далі потрібно ввести старший ступінь для другого багаточлену і ввести його коефіцієнти. Програма також автоматично виведе його у зручному вигляді на екран. Оскільки ділення багаточленя з меншим ступенем на багаточлен з більшим ступенем неможливе, в разі такого випадку програма видасть відповідне повідомлення про неможливість розрахунків.
Коли всі вхідні дані введені, програма виконує ділення багаточленів і виводить отримані результати, якими є результат ділення у вигляді багаточлена, та остаток від ділення, також у вигляді багаточлена, представленому в зручному для сприйняття вигляді.
Зображення кінцевого результату обчислень показане на рис. 3.4.
При необхідності повторного ділення багаточленів з іншими вхідними параметрами після отримання результатів можна натиснути клавішу Enter – при цьому вікно програми буде очищено, і можна буде розпочати ввід нових даних.
Вихід з програми виконується після отримання результатів при натисненні клавіші Esc.

Рис. 3.4 – Вивід результатів розрахунків
4 ПРИКЛАД РОБОТИ ПРОГРАМНОГО КОМЛЕКСУ
Розглянемо приклад роботи програмного комплексу на наступних вхідних даних:
1) ступінь першого багаточлену: 3;
2) коефіцієнти: 8 16 -2 4;
тобто перший багаточлен має наступний вигляд:

3) ступінь другого багаточлену: 2;
4) коефіцієнти: 4 -2 1;
тобто другий багаточлен має наступний вигляд:

На рисунку 4.1 показано результат роботи програми, запущеної з вказаними параметрами.

Рис. 4.1 – Результат роботи програми
Результатом роботи програми є вивід двох багаточленів: результату ділення та остатку від ділення. Результатом ділення також може бути багаточлен з нульовими коефіцієнтами, в випадку, якщо ділення неможливе на першому ж кроці.
Виконаємо перевірку отриманих результатів за допомогою середовища Mathcad. Умножимо отриманий результат ділення на дільник і додамо остаток, при цьому при правильних розрахунках повиннен вийти перший багаточлен. Скористаємося функцією Mathcad «expand» для розвернення отриманого виразу в поліном:

Оскільки отриманий вираз ідентичний першому багаточлену, отримано вірний результат.
Ділення неможливе за визначенням у випадку, якщо введено багаточлени такі, що ступінь другого більша за ступінь першого. В такому випадку програма видає відповідне повідомлення. Вікно з прикладом такого повідомлення показане на рис. 4.2.

Рис. 4.2 – Вікно програми з повідомленням про неможливість ділення
ВИСНОВКИ
1. В процесі виконання курсової роботи розглянуті методи виконання цілочисельного ділення з остатком двох багаточленів довільних ступенів.
2. Розроблено алгоритм для програмної реалізації цілочисельного ділення двох багаточленів, заданих користувачем у вигляді коефіцієнтів при ступенях невідомих.
3. Створений програмний комплекс дозволяє для довільних двох багаточленів виконувати цілочисельне ділення з остатком, що значно полегшує аналогічні ручні розрахунки та може бути навчальним прикладом для людей, що вивчають правило ділення багаточленів «у стовбчик».
ПЕРЕЛІК ПОСИЛАНЬ
1 Шувалова Э. З., Агафонов Б. Г., Богатырёв Г. И. Повторим математику. М: Высшая школа, 1968г.
2 С. М. Олехник, М. К. Потапов, П.И. Пасиченко Уравнения и неравенства. Нестандартные методы решения: Справочник.
3 Выгодский М.Я. Справочник по элементарной математике. М: Наука, 1976 – 335 с.
RESUME






