Нахождение неизвестного слагаемого. a – слагаемое, x – слагаемое, b – сумма.
a+x=b, x = b – a; x + a = b, x = b – a.
Нахождение неизвестного уменьшаемого. x – уменьшаемое, a – вычитаемое, b – разность.
x – a = b, x = b + a.
Нахождение неизвестного вычитаемого. a – уменьшаемое, x – вычитаемое, b – разность.
a – x = b, x = a - b.
Нахождение неизвестного множителя. a – множитель, x – множитель, b – произведение.
a × x = b, x = b: a, x × a = b, x = b: a.
Нахождение неизвестного делимого. a – делитель, x – делимое, b – частное.
x: a = b, x = b × a.
Нахождение неизвестного делителя. a – делимое, x – делитель, b – частное.
a: x = b, x = a: b.
Сложение и вычитание — действия первой ступени (I). Умножение и деление — действия второй ступени (II). Возведение в степень — действие третьей ступени (III). Сначала выполняются действия высших ступеней, а затем низших ступеней (III, II, потом I). Если в выражение есть скобки, то сначала производятся действия в скобках, соблюдая ступени действий.
Степень с натуральным показателем. an
Произведение n множителей, каждый из которых равен a.
a – основание степени, n- показатель степени.
a 1 = а.
ат ·а" = ат + п.
ат:а" = аm-n.
(ат)п = атп.
Уравнения и системы уравнений.
Тождеством называется равенство верное при любых значениях входящих в него переменных.
Уравнением с одним неизвестным называется равенство, содержащее обозначенное буквой неизвестное число, которое требуется найти.
Корнем уравнения называется число, подстановка которого вместо буквы превращает уравнение в верное равенство.
Решить уравнение - это, значит, найти все его корни или убедится, что их нет.
Равносильными называются уравнения, у которых одни и те же корни.
ax+b=0 – линейное уравнение с одной переменной,
x – переменная, a,b- некоторые числа.
Если a≠0, то единственный корень x= 
Если a=0 и b≠0, то уравнение не имеет корней,
Если a=0 и b=0, то уравнение имеет бесконечное множество корней.
Квадратный трехчлен ах2 + bх + с (a≠0) и квадратное уравнение ах2 +bх + с = 0 (a≠0) D — дискриминант, xl и х2 — корни.
D = b2-4ac. 
Если коэффициент b — четный, удобно пользоваться формулами:
Неполные квадратные уравнения.
Если в квадратном уравнении b=0 или c = 0 или b=c=0, то уравнение называется неполным квадратным уравнением.
ах2 + с = 0; ах2 +bх = 0; ах2 = 0.
Разложение квадратного трехчлена на множители (х1, х2 — корни)
Если D > О, то ах2 + bх + с = а(х — х1)(х - х2).
Если D= О, то ах2 + bх + с = а(х — х1)2.
Теорема Виета (свойство корней квадратного уравнения)
Если х1 и х2 — корни квадратного уравнения ах2 +bх + с = 0, то
.
Теорема, обратная теореме Виета (признак квадратного уравнения)
Если m и n таковы, что 
, то числа m и n – корни квадратного уравнения ах2 +bх + с = 0.
Системой двух уравнений с двумя неизвестными называется два уравнения, которые рассматриваются совместно и в которых неизвестные числа одни и те же.
Решением системы называется пара чисел, которая при подстановке в каждое из уравнений системы обращает его в верное равенство.
Решить систему уравнений - это значит найти все её корни или доказать, что их нет.
Способ подстановки: выражаем одно неизвестное из одного урав-нение через другое неизвестное, подставляем в другое уравнение, решаем полученное уравнение с одним неизвестным, полученное значение неизвестного подставляем в первое и находим второе неизвестное.
Способ сложения: рассматриваем новую систему, в которой при одном из неизвестных коэффициенты равные, но разные по знаку, для этого умножаем уравнения на различные числа, складываем почленно полученные равенства, получаем уравнение с одной переменной, находим её и подставляем полученное значение в уравнения системы, получаем вторую переменную.
Графический способ: строим графики функций, задающих каждое из уравнений системы, находим координаты точек пересечения построенных графиков (если они есть), абсцисса и ордината точек пересечения – решение системы. Графический способ дает приближенные результаты.
Функции и графики функций.
y = f(x)
Функция – это зависимость переменной y от переменной x, при которой каждому значению переменной x соответствует единственное значение переменной y.
x – независимая переменная, аргумент,
y – зависимая переменная, функция.
Область определения функции – все значения аргумента,
Область значений функции – все значения зависимой переменной.
График функции – множество точек координатной плоскости, абсциссы которых равны значению аргумента, а ординаты – значению функции.
Способы задания функции: графический, табличный, рекуррентный.
Функция называется возрастающей на промежутке, если большему значению x соответствует большее значение f(x), функция называется убывающей на промежутке, если большему значению x соответствует меньшее значение f(x).
Функция называется четной, если при изменении знака x, знак y не изменяется, т.е. f(-x) = f(x), график симметричен относительно оси ординат, функция называется нечетной, если при изменении знака x знак y меняется на противоположный, т.е. f(-x)= -f(x), график симметричен относительно начала координат.
Координатная плоскость
Две перпендикулярные координатные прямые x и y, которые пересекаются в начале отсчета, точке О называют системой координат на плоскости, O –начало координат.
Плоскость, на которой выбрана система координат, называют координатной плоскостью.
Каждой точке на координатной плоскости соответствует пара чисел - её координаты, каждой паре чисел соответствует одна точка плоскости, для которой эти числа являются координатами.
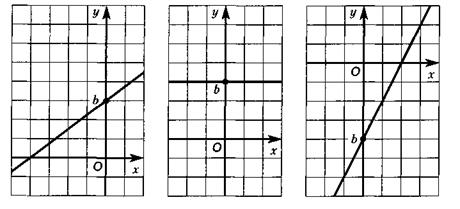
Линейная функция (график — прямая)
y=kx+b, k,b- некоторые числа.
Область определения - все действительные числа
I. у = kx.
1) k >0 2) k = 0 3) k < 0
II. у = kx + b.
1) k > О, b > 0 2) k = 0, b > 0 3) k > 0, b < О
Квадратная функция (график — парабола)
y=x2
Область определения – все действительные числа.
Функция четная, точка (0;0) – вершина параболы.
у = ах2, (а≠ 0).
1) а > 0 2) а < 0
Обратная пропорциональность (график - гипербола)
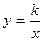, k – действительное число.
Область определения - все действительные числа, кроме 0
1) k > 0
3) k < 0
Квадратный и арифметический корень.
Квадратный и арифметический квадратный корень.
Квадратным корнем из числа a, называется число квадрат которого равен a.
Арифметическим квадратным корнем из числа a, называется неотрицательное число квадрат которого равен a.
.
Погрешности.
Приближенные вычисления и погрешности.
Округление: => с недостатком, если отбрасываемая цифра менее 5, => с избытком, если отбрасываемая цифра больше 5. Округлить:
а) до десятых 12,34; 12,34»12,3
б) до сотых 3,2465; 3,2465»3,25
в) до тысячных 3,4335; 3,4335»3,434
г) до тысяч 12375; 12375»12000.
Абсолютная погрешность - разность между точным значением и приближённым значением числа, взятая по модулю.
Относительная погрешность а/½a½ — отношение абсолютной погрешности к величине приближённого числа (выражается в процентах).
Прогрессии.
Ряд чисел, в котором для каждого числа можно указать его порядковый номер в этом ряду, называют числовой последовательностью.
Арифметической прогрессией называется такая числовая последовательность, каждый член которой, начиная со второго равен предыдущему, сложенному с некоторым действительным числом – d.
Геометрической прогрессией называется такая числовая последовательность, каждый член которой, начиная со второго равен предыдущему, умноженному на некоторое, не равное нулю действительное число – q.
Арифметическая прогрессия
Обозначения: (а„): а1, а2,... аn
a 1 — первый член прогрессии
аn — п-й член прогрессии
d — разность арифметической прогрессии
Sn — сумма п первых членов прогрессии
Если, d = 0, то 
Геометрическая прогрессия
Обозначения: (bn): b1 b2... bn,....
b1 — первый член прогрессии
bn — n -й член прогрессии
q — знаменатель геометрической прогрессии
Sn — сумма п первых членов прогрессии
Сумма S бесконечной геометрической прогрессии, у которой 
ГЕОМЕТРИЯ.
Отрезок и угол.
Отрезок — часть прямой, ограниченная с двух сторон точками. Точки называются концами отрезка.
Точка отрезка, делящая его пополам, называется серединой отрезка.
Луч — прямая, выходящая из заданной точки и уходящая в бесконечность.
Два отрезка считаются равными, если при наложении они совмещаются всеми точками.
Длина отрезка — число, получаемое в результате измерения, это число показывает сколько раз единица измерения и её части укладываются в измеряемом отрезка.
Свойства длины:
- Равные отрезки имеют равные длины,
- Меньший отрезок имеет меньшую длину,
- Если отрезок разделен точками на части, то длина всего отрезка равна сумме длин его частей.
Угол — фигура образованная двумя лучами или отрезками (стороны угла), выходящими из одной точки (вершина угла).
Два угла называются равными, если при наложении они совпадают.
Развёрнутый угол — угол, одна сторона которого является продолжением другой.
Смежными углами называются два прилежащих угла, не совпадающие стороны которых образуют прямую.
Сумма смежных углов равна 180°
Если два смежных угла равны между собой, то каждый из них называется прямым.
Вертикальные углы — у которых стороны являются продолжением сторон другого. Они образуются при пересечении двух прямых.
Вертикальные углы равны.
1° — единица измерения угла в градусной системе — это угол, составляющий 1/360 часть полного угла. Дуга центрального угла в 1°составляет 1/360 часть дуги окружности.
1’ — 1/60 часть градуса, (одна минута). 1" — 1/3600 часть градуса (одна секунда). 1 рад — это такой центральный угол, дуга которого равна радиусу окружности.
360° эквивалентно 2p рад. Следовательно:
Развёрнутый угол — 180°, прямой угол — 90°, острый угол — угол содержащий < 90°, тупой угол — угол содержащий > 90°, но <180°
Градусная мера угла – это положительное число, которое показывает сколько раз градус и его части укладываются в данный угол.
Свойства градусной меры угла:
- Равные углы имеют равные градусные меры,
- Меньший угол имеет меньшую градусную меру,
- Если угол делится лучами на части, то градусная мера всего угла равна сумме градусных мер его частей.
Треугольник и его свойства.
Треугольник – фигура, состоящая из трех точек, не лежащих на одной прямой и попарно соединенных отрезками.
Точки – вершины, отрезки – стороны треугольника.
Остроугольный D — если все углы острые. Тупоугольный D — если один из его углов тупой. Прямоугольный D — если один из углов прямой. Стороны образующие прямой угол — катеты. Третья сторона — гипотенуза. Равнобедренный D — две стороны равны. Равносторонний D все три стороны равны. Теорема: Во всяком D сумма углов равна 180° или p радиан.
Высота треугольника -это перпендикуляр, опущенный из любой вершины D на противолежащую сторону или на её продолжение. Три высоты D всегда пересекаются в одной точке, которая называете
ортоцентром. Ортоцентрв: тупоугольном D — вне D; остроугольном D — внутри D; прямоугольном D — вершина прямой угла.
Медиана треугольника -отрезок, соединяющий произвольную его вершину с серединой противолежащей стороны. Три медианы D пересекаются в одной точке, эта точка всегданаходится внутриD, являясь его центром тяжести. Свойство: Точка пересечения медиан делит каждую медиану в соотношении 2:1 (считая от вершин).
В прямоугольном D медиана, опущенная на гипотенузу, равна половине гипотенузы.
Биссектриса треугольника -называется отрезок биссектрисы любого угла этого D от вершины до пересечения с противопо-ложной стороной. Все три биссектрисы D пересекаются в одной точке, лежащей всегда внутри D и являющейся центром вписанной окружности.
Средняя линия треугольника – это отрезок, который соединяет середины двух сторон этого треугольника.
Свойства средней линии D:
· средняя линия D параллельна его основанию,
· средняя линия D равна половине его основания.
Внешний угол треугольника – смежный с любым внутренним углом.
Всякий внешний угол D равен сумме двух внутренних, не смежных с ним.
Если два угла одного D соответственно равны двум углам другого D, то третьи углы равны. Сумма острых углов в прямоугольном D равна 90°. В равнобедренном прямоугольном D каждый острый угол равен 45°.
Теорема: если в прямоугольном D один из острых углов равен 30", то лежащий против этого угла катет составляет половину гипотенузы.
Признаки равенства двух треугольников.
Два D равны, если у них соответственно равны:
I. — Две стороны и угол между ними.
II. — Два угла и прилежащая к ним сторона.
III. — Три стороны.
IV. — Два угла и сторона, противолежащая одному из них.
V. — Две стороны и угол, лежащий против большей из них.)
Два прямоугольных D равны в следующих четырёх случаях
(частные случаи I — V признаков):
1) Если катеты одного D соответственно равны катетам другого D
2) Если катет и прилежащий к нему острый угол одного D соответ-ственно равен катету и прилежащему к нему острому углу другого D
3) Если гипотенуза и острый угол одного D соответственно равны гипотенузе и острому углу другого D.
4) Если гипотенуза и катет одного D соответственно равны гипотенузе и катету другого D.
Косинусом острого угла прямоугольного D называется отношение прилежащего катета к гипотенузе
Синусом острого угла прямоугольного D называется отношение противолежащего катета к гипотенузе.
Тангенсом острого угла прямоугольного D называется отношение противолежащего катета к прилежащему катету.
Котангенсом острого угла прямоугольного D называется отношение прилежащего катета к противолежащему катету.
Теорема Пифагора: В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов, c2= a2 + b2
Обратная теорема: Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный.
Признаки равнобедренного треугольника:
· если равны углы при основании, то D равнобедренный,
· если в D биссектриса и высота, высота и медиана, медиана и биссектриса, проведенные из вершины равны, то D равнобедренный.
Свойства равнобедренного треугольника:
· если D равнобедренный, то углы при основании равны,
· если D равнобедренный, то биссектриса и высота, высота и медиана, медиана и биссектриса, проведенные из вершины равны.
Подобие треугольников.
Если углы одного из двух данных D соответственно равны углам другого, то те их стороны, которые лежат против равных углов, называются сходственными сторонами. Два треугольника называются подобными, если их соответственные углы равны и стороны одного пропорциональны сходственным сторонам другого.
Признаки подобия D. Два треугольника подобны если:
1. Два угла одного D соответственно равны двум углам другого D.
2. Две стороны одного D соответственно пропорциональны двум сторонам другого D и углы, заключённые между этими сторонами равны.
3. Три стороны одного D соответственно пропорциональны трём сторонам другого D.
Теорема: В любом D против большей стороны лежит больший угол, обратно - против большего угла лежит большая сторона.
В прямоугольном D гипотенуза больше катета.
Неравенство треугольника: каждая сторона D меньше суммы двух других сторон.
Теорема косинусов: Квадрат стороны D равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними. a2 = b2 + c2 – 2bc cosa
Теорема синусов: стороны D пропорциональны синусам противолежащих углов.
Площадь треугольника:
Для вычисления площади треугольника можно воспользоваться одной из следующих формул:
1. S = (l/2)bhb (b — основание D, hb —соответствующая высота)
2. S = (l/2)absinC, где а и b — стороны, С — угол между ними.
3. S = рг, где р = (а + b + с)/2 полупериметр, г — радиус вписанной
окружности.
4. S = abc/4R, где а, Ь, с —стороны, R — радиус описанной
окружности.
5. 
(формула Герона), где а, b, с —
стороны, р — полупериметр.
Площади подобных треугольников относятся как квадраты их сходс-твенных линейных элементов: сторон, высот, медиан, биссектрис и т. д.
Четырехугольники: параллелограмм, прямоугольник, ромб, квадрат, трапеция.
Параллелограмм – это четырехугольник, у которого противолежащие стороны попарно параллельны.
Признаки параллелограмма:
· Если диагонали четырехугольника пересекаются и точкой пресечения делятся пополам, то этот четырехугольник параллелограмм.
· Если противолежащие стороны попарно равны, то четырехугольник параллелограмм,
· Если две противолежащие стороны равны и параллельны, то четырехугольник параллелограмм,
· Если противолежащие углы равны.
Свойства параллелограмма:
· Диагонали пересекаются и точкой пересечения делятся пополам,
· Противолежащие стороны равны,
· Противолежащие углы раны.
Площадь параллелограмма.
S = a × ha (a –сторона, ha – высота параллелограмма).
S = a × b × sin g (a, b – стороны, g- угол между ними).
S = (d1 × d2 ×sin j)/2 (d1, d2 – диагонали параллелограмма, j- угол между ними).
Прямоугольник – это параллелограмм, у которого все углы прямые.
Свойство прямоугольника:
· Диагонали прямоугольника равны,
Площадь прямоугольника:
S = a × b (a, b –стороны прямоугольника).
S = (d2 ×sin a)/2 (d – длина диагонали прямоугольника, a - угол между диагоналями).
Ромб – это параллелограмм, у которого все стороны равны.
Свойства ромба:
· Диагонали ромба пересекаются под прямым углом,
· Диагонали являются биссектрисами углов.
Площадь ромба:
S = a × ha (a –сторона, ha – высота ромба).
S = a2 × sin g (a – сторона, g- угол ромба).
S = (d1 × d2)/2 (d1, d2 – диагонали ромба).
Квадрат – это параллелограмм, у которого все углы прямые и все стороны равны.
Свойства квадрата:
· Диагонали равны,
· Диагонали пересекаются под прямым углом,
· Диагонали являются биссектрисами углов.
Площадь квадрата:
S = a2 (a –сторона квадрата).
S = d2/2 (d– диагональ квадрата).
Трапеция - четырёхугольник, две противоположные стороны которого параллельны, а две другие не параллельны. Параллельные стороны — основания, не параллельные — боковые стороны, h — высота; MN — средняя линия трапеции. Средняя линия - соединяет середины боковых сторон. Средняя линия равна полусумме оснований и параллельна им: m = (а + b)/2. Трапеция, у которой боковые стороны равны, называется равнобедренной. В равнобедренной трапеции углы при основании равны. Трапеция, у которой хотя бы один угол прямой, называется прямоугольной.
Площадь трапеции:
S = l/2(a+b)h (a,b- основания, h – высота трапеции).
S=mh. (m – средняя линия, h - высота трапеции).
