АЛГЕБРА
Обыкновенные и десятичные дроби.
Если 1 делится на несколько частей (b) и берется какое – то число таких частей (a), то получится обыкновенная дробь, a - числитель, b - знаменатель. 
Если a<b, то дробь правильная, если a>b, то дробь неправильная.
Если знаменатели дробей одинаковые, то больше та, у которой числитель больше.
Любое натуральное число a можно представить в виде дроби с любым натуральным показателем n по формуле 
Сумму натурального числа и правильной дроби, записанную без знака «+», называют смешанным числом.
Запись неправильной дроби в виде смешанного числа называют выделением целой части дроби.
Действия над дробями:
1.Сложение дробей с одинаковым знаменателем: 
2.Вычитание дробей с одинаковым знаменателем: 
3.Умножение дробей: 
4.Деление дробей: 
Десятичной дробью называется десятичная запись числа, в которой есть разряд единиц и разряды правее разряда единиц. При записи правее разряда единиц ставится запятая.
Умножение и деление десятичной дроби на 10n. 15,45· 10=154,5; 32,3·100=3230 запятая переносятся вправо на число нулей.
184,35:100=1,8435; 3,5:100=0,035 запятая переносится влево на число нулей.
Сложение и вычитание десятичных дробей. Сложение и вычитание выполняется, так же как и сложение и вычитание натуральных чисел, по разрядам, начиная с младших. Пустые клетки можно заполнить нулями.
Умножение десятичных дробей.
1) Перемножить дроби, не обращая внимания на запятые, как целые числа.
2) Отделить «,» справа столько знаков, сколько их было во 2 множителе и 1 множимом вместе.
Деление десятичных дробей.
Деление выполняется, так же как и деление целых чисел, увеличивая делитель и делимое в 10, 100, 1000 и т.д. раз, чтобы избавиться от запятой.
Периодическая десятичная дробь.
чистая 2,36363636... - период начинается сразу за запятой смешанная 0,5232323... - между «,» и первым периодом есть несколько цифр.
Числа, которые можно представить в виде 
, где m – целое, n – натуральное, называются рациональными числами. Иррациональным числом называется бесконечная непериодическая десятичная дробь. Числа рациональные и иррациональные образуют множество действительных чисел.
Делимость чисел.
Всякое число, кроме единицы, которое делится только на один н само на себя, называется простым.
Число, которое делится не только на единицу и само на себя, но
ещё и на другие числа, называется составным.
Число 1 занимает особое положение..
Простые числа: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29 и т.д.
Составное число разлагается на простые множители единственным образом.
Пример: 5600=2·2·2·2·2·5·5·7, или 5600=25·52·7
Признаки делимости
На 10. На 10 делятся все те и только те числа, которые оканчиваются нулями.
На 2 и 5 делятся все те и только те числа, у которых последняя цифра выражает число, делящееся соответственно на 2 или на 5.
На 3 и 9 делятся все те и только те числа, у которых сумма цифр делится соответственно на 3 или на 9.
Делителем данного числа называется число, на которое данное число делится без остатка.
НОД — Наибольшим общим делителем нескольких чисел называется наибольшее число, на которое все данные числа делятся без остатка. НОД (a, b)
Как найти НОД? Пример 1. Найти НОД чисел 210, 1260 и 245,
Разложим эти числа на простые множители.
210 = 2·3·5·7; 1260 = 22·32·5·7; 245 = 5·72 НОД будет 5·7= 35.
Если в остатке 0 => последний делитель и есть НОД данных чисел. Следовательно, 23 есть НОД чисел 391 в 299.
НОК — наименьшим общим кратным нескольких чисел называется самое меньшее натуральное число, которое делится на каждое из данных чисел. НОК (a, b)
Как найти НОК? Пример 1. Найти НОК 72 и 108.
Разложим данные числа на множители: 72=23·32; 108=22·33.
Множители числа 108 (это удобнее, так как число 108 больше 72), умножая на недостающие простые множители числа 72, т.е. 2, получим: НОК(72,108) = 23·33 = 216.
Например: НОК(60,120,40) =120, НОК(7,8,11) = 7·8·11=616.
Пропорции и проценты.
Частное двух чисел называется отношением этих чисел. 
Равенство двух отношений называется пропорцией. 
a, b – крайние члены, c, d – средние члены пропорции.
Основное свойство пропорции: 
Прямая пропорциональность величин: 
, k = const (при уве-личении одной величины, другая увеличивается во столько же раз).
Обратная пропорциональность величин: 
, k = const (при увеличении одной величины, другая уменьшается во столько же раз).
Процентом, какого- либо числа называется сотая часть этого числа(%).
Нахождение % данного числа. p % числа а равно P. 
Нахождение числа по его %.
если р % какого-то числа составляют а, то всё число равно Р.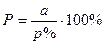 
Нахождение процентного отношения двух чисел.
Процентное отношение двух чисел – это отношение, выраженное в сотых долях.
Одночлены и многочлены.
Одночленом называется произведение чисел, букв и их степеней, а также сами числа, буквы и их степени.
Стандартный вид одночлена - один числовой множитель, стоящий на первом месте, произведение одинаковых букв записано в виде степени.
Числовой множитель – коэффициент одночлена,
Степень одночлена – сумма степеней входящих в него букв.
Многочлен – алгебраическая сумма одночленов.
Стандартный вид многочлена – все одночлены записаны в стандартном виде.
Степень многочлена – наибольшая из степеней входящих одночленов.
Умножение и деление одночленов и многочленов:
1. Умножение одночленов: 
2. Умножение одночлена на многочлен: 
3. Умножение многочлена на многочлен:
Деление одночлена и многочлена на одночлен производится аналогично: деление числовых множителей, деление входящих в них букв.
Формулы сокращенного умножения
(a + b)2=a2 + 2ab + b2.
(a-b)2= a2-2ab + b2.
(a-b)(a + b) = a2-b2.
(a + b)(a2 -ab + b2) = a3 + b3.
(a - b)(a2 + ab + b2) = a3-b3.
(a + b)= a3 + 3a2b + 3ab2 + b3.
(a-b)= a3-3a2b + 3ab2-b3.
