Краткая теория эксперимента

Министерство образования и науки

Российской федерации

Ростовский государственный

Строительный университет

 

 

Утверждено

на заседании кафедры физики

«21» сентября 2004 г.

 

Методические указания

 

К лабораторной работе № 12

 

 

«ИЗУЧЕНИЕ ЗАТУХАЮЩИХ КОЛЕБАНИЙ ФИЗИЧЕСКОГО МАЯТНИКА»

 

Ростов-на-Дону

 

 

УДК 531.383

Методические указания к лабораторной работе № 12 «Изучение затухающих колебаний физического маятника». – Ростов н/Д: Рост. гос. строит. ун-т, 2005. – 8 с.

 

Содержат необходимый теоретический материал, сведения о порядке выполнения работы и оформления ее результатов.

Предназначены для выполнения лабораторной работы по программе курса общей физики для студентов всех специальностей.

 

Составитель: доц. А.Н.Павлов

Рецензент: доц. Ю.И.Гольцов

 

Редактор К.Е.Гладких

Темплан 2005, поз. 162

Подписано в печать 29.10.04

Формат 60х84 1/16. Бумага писчая. Ризограф. Уч.-изд.л. 0,5.

Тираж 50 экз. Заказ

___________________________________________________________

 

Редакционно-издательский центр

Ростовского государственного строительного университета

334022, Ростов-на-Дону, ул.Социалистическая, 162.

 

© Ростовский государственный

строительный университет, 2005

 

 

Лабораторная работа №12

 

ИЗУЧЕНИЕ ЗАТУХАЮЩИХ КОЛЕБАНИЙ ФИЗИЧЕСКОГО МАЯТНИКА

 

Цель работы: ознакомление с основными закономерностями затухающих колебаний на примере колебаний физического маятника.

Приборы и принадлежности: физический маятник, шкала для определения амплитуд отклонения маятника.

 

Краткая теория эксперимента

Рассмотрим физический маятник (рис.1), совершающий малые колебания в вязкой среде (в нашем случае воздухе).

 

 

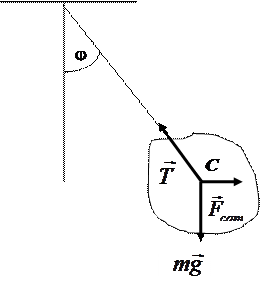Рис.1

Если колебания достаточно малы (j «1 рад), то сила сопротивления маятнику F_cопр со стороны жидкости или газа будет пропорциональна его скорости (), а величина возвращающей силы F_в пропорциональна смещению х маятника с массой m и длиной l ().

Если пренебречь трением в подвесе, дифференциальное уравнение

движения маятника при k=mg/l будет иметь вид:

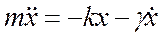. (1)

Уравнение (1) может быть приведено к каноническому виду

, (2)

где .

Величина b называется коэффициентом затухания; w₀ - циклической частотой свободных колебаний маятника в отсутствие сил трения. Легко убедиться подстановкой, что решением уравнения (2) будет

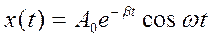, (3)

где - начальное отклонение маятника, .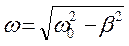

График функции (3),описывающей затухающие колебания, дан на рис.2

 

 

Рис.2

Как видно из решения (3), наличие трения (b¹0) приводит к затуханию колебаний и уменьшению частоты (увеличению периода). При b = w₀ колебания могут прекратиться, это возможно при очень большой вязкости среды или малой массе маятника. Согласно (3) амплитуды максимальных отклонений уменьшаются по закону:

, (4)

где Т - условный период затухающих колебаний.

Легко видеть, что отношение двух последующих амплитуд, разделенных периодом, оказывается величиной постоянной.

. (5)

Величина D - называется декрементом затухания;

l=lnD=bT - логарифмический декремент затухания.

Ряд убывающих амплитуд (4) может быть записан в виде убывающей геометрической прогрессии, основанием которой является декремент, т.е.

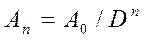. (6)

II. ПРАКТИЧЕСКАЯ ЧАСТЬ

1. Определите декремент затухания D. Для этого отклоните маятник
до А₀ = 30 см и без толчка отпустите его. Дав ему совершить N=10 колебаний, замерьте амплитуду А_N. Вычислите логарифмический декремент затухания и определите декремент D.

. (7)

Oпыт повторите три раза и вычислите среднее значение декремента D.

2. Рассчитайте и занесите в таблицу теоретические значения четных амплитуд колебаний маятника A₂, A₄, …, A₂₀ при A₀ =30 см. Для этого расчета удобно воспользоваться формулой (6), переписанной в рекуррентном виде

. (8)

3. Для экспериментального исследования зависимости от времени амплитуды колебаний маятника установите начальную амплитуду A₀ =30 см и без толчка отпустите маятник. С помощью измерительной шкалы определите и занесите в табл. 1 экспериментальные значения четных амплитуд колебаний маятника A₂, A₄, …, A₂₀. Опыт повторите не менее трех раз.

Таблица 1

	A2,см	A4,см	A6, см	A8, см	A10, см	A12, см	A14, см	A16, см	A18,см	A20,см
Теорет. ампл.
№ эксп
Средн. эксп. ампл.

 

4. Постройте на одном чертеже графики экспериментального и теоретического затухания колебаний физического маятника.

 

 

Контрольные вопросы

 

1. При каких силах, действующих на маятник, амплитуда затухающих колебаний уменьшается с течением времени по показательному закону?

2. Напишите дифференциальное уравнение движения колеблющегося
маятника и его решение.

3. Дайте определение декремента затухания и раскройте его физический
смысл.

4. В каком случае движение маятника перестает быть колебательным?

5. Как сказывается сила трения в подвесе на виде
экспериментальной зависимости амплитуды колебаний от времени?

6. Для вопросов, приведенных в табл. 2, выберите правильный

вариант ответа.

Таблица 2

	Период колебаний маятника равен 1 секунде. За какое время он проходит первую половину расстояния от положе­ния равновесия до максимального отклонения?
А	0,5 с
Б	0,33 с
В	0,25 с
Г	0,167 с
	Небольшой шар на нити длиной 20 см совершает свободные колебания с амплитудой 5 см. Как изме­нится период колебаний маятника при увеличении амплитуды колебаний до 10 см?
А	Уменьшится в 2 раза.
Б	Увеличится в 4 раза.
В	Не изменится.
Г	Немного уменьшится.
	Для определения периода свободных колебаний математического маятника была измерена длина подвеса. Она оказалась равной 50 ± 2 см. С какой от­носительной погрешностью может быть рассчитан период колебаний маятника на основе результатов этих измерений?

Окончание табл. 2

А	4×10-2
Б	2×10-2
В	0,2
Г	0,1
	Ведро заполнено водой, подвешено на длинной ве­ревке и совершает свободные колебания. В его дне есть небольшое отверстие. Как изменяется период колебаний по мере вытекания воды?
А	Непрерывно увеличивается.
Б	Непрерывно уменьша­ется.
В	Остается неизменным.
Г	Сначала уменьшается, затем увеличивается.
	Груз, поднимаемый с помощью крана, в результате быстрого поворота крана отклонился от положения равновесия на 8° и начал раскачиваться. Какова примерно максимальная скорость груза, если длина троса 18 м? (sin 8° = 0,14, cos 8° = 0,99.)
А	1,4 м/с
Б	2,67 м/с
В	1,9 м/с
Г	1,32 м/с
	Имеются два одинаковых камертона. Первый за­креплен на обычной деревянной подставке, второй установлен на деревянном ящике — резонаторе. По камертонам делаются одинаковые удары молоточ­ком. Какой камертон будет звучать громче и какой дольше?
А	Первый громче и дольше.
Б	Второй громче и дольше.
В	Первый громче, второй дольше.
Г	Второй громче, пер­вый дольше.
	Мимо неподвижного наблюдателя проехал автомо­биль с включенной сиреной. При приближении ав­томобиля наблюдатель слышал более высокий тон звука, а при удалении более низкий тон звука. Ка­кой эффект будет наблюдаться, если сирена будет неподвижной, а мимо нее проедет наблюдатель?
А	При приближении тон повысится, при удалении пони­зится,
Б	При приближении и при удалении тон останется неиз­менным.
В	При приближении тон понизится, при удалении повы­сится
Г	И при приближении, и при удалении тон понизится.