1. Используя определение степени, свойства степеней привести показательное уравнение к виду k f(x) = k q(x) или k f(x) = m, где m-постоянное число.
2. В зависимости от вида уравнения использовать один из вариантов:
а) используя утверждение: если равны степени и основания степеней, то равны и показатели степеней, перейти от уравнения k f(x) = k q(x) к уравнению f(x) = q(x)
б) Уравнение вида k f(x) = m следует прологарифмировать по основанию k.
Алгоритм решения логарифмических неравенств
1. Найти область определения неравенства (подлогарифмическое выражение больше нуля).
2. Представить (если возможно) левую и правую части неравенства в виде логарифмов по одному и тому же основанию.
3. Определить, возрастающей или убывающей является логарифмическая функция: если a > 1, то возрастающая; если 0 < a < 1, то убывающая.
4. Перейти к более простому неравенству (подлогарифмических выражений), учитывая, что знак неравенства сохранится, если функция возрастает, и изменится, если она убывает.
Если a > 1 и 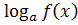 <
< 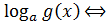
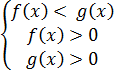
Если 0< a < 1 и 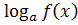 <
< 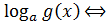
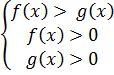
Критерии оценки решения логарифмических неравенств:
«5»: Правильно определена область определения неравенства; правильно представлены левая и правая части неравенства в виде логарифмов по одному и тому же основанию; определено, возрастающая или убывающая функция; решено простое неравенство; записан ответ.
«4»: В решении имеются неточности: неправильно определена возрастающая или убывающая функция; не записан ответ.
«3»: В решении неправильно определена область определения неравенства или неправильно решено простое неравенство.
«2»: Грубые ошибки в решении: не найдена область определения; неправильно определена возрастающая или убывающая функция; ошибки в решении простого неравенства.
Решение логарифмических уравнений
1.Используя определение логарифма, его свойства, привести уравнение к виду lоga f(x)=lоga q(x) или lоga f(x)=k, где k - постоянное число, причем f(x)>0, q(x) >0
2.Перейти к системе на основании того, что если логарифмы с одинаковыми основаниями двух выражений равны, то равны и сами выражения.
3.Решить получившуюся систему.
СПИСОК ЛИТЕРАТУРЫ
ОСНОВНАЯ
1. Алимов, Ш.А, Калягин, Ю.М. Алгебра и начала анализа: учебник для 10-11 классов общеобразовательных учреждений. [Текст] М.: Просвещение, 2011.
2. Атанасян, Л.С. и др. Геометрия: учебник для 10-11 классов средних школ. [Текст] М.: Просвещение, 2011.
3. Богомолов, Н.В., Самойленко, П.И. Математика[Текст]: М.: Дрофа, 2009.
4. Богомолов, Н.В., Сергиенко, Л.Ю. / Сборник дидактических заданий по математике. [Текст] М.: Дрофа, 2009.
5. Богомолов, Н.В. «Практические занятия по математике», [Текст] М.: Высшая школа, 2009.
6. Башмаков,М.И. Алгебра и начала математического анализа (базовый уровень). 10 кл. [Текст] – М., 2009.
7. Луканкин,Г.Л., Луканкин, А.Г. Математика. Ч. 1: учебное пособие для учреждений начального профессионального образования. [Текст] – М., 2004.
ДОПОЛНИТЕЛЬНАЯ
1. Колягин,Ю.М. и др. Математика (Книга 1). [Текст] – М., 2003.
2. Колмогоров,А.Н. и др. Алгебра и начала анализа. 10 (11) кл. [Текст] – М., 2008.
3. Колягин,Ю.М. и др. Математика (Книга 2). [Текст] – М., 2003.
Рецензия
на «Методические рекомендации по организации самостоятельной учебной работы студентов по учебной дисциплине математика»






