К началу выполнения арифметического действия операнды операции помещаются в соответствующие регистры АЛУ.
При сложении и вычитании сначала производится подготовительная операция, называемая выравниванием порядков. В процессе выравнивания порядков мантисса числа с меньшим порядком сдвигается в своем регистре вправо на количество разрядов, равное разности порядков операндов. После каждого сдвига порядок увеличивается на единицу.
В результате выравнивания порядков одноименные разряды чисел оказываются расположенными в соответствующих разрядах обоих регистров, после чего мантиссы складываются или вычитаются.
В случае необходимости полученный результат нормализуется путем сдвига мантиссы результата влево. После каждого сдвига влево порядок результата уменьшается на единицу.
Пример. Сложить двоичные нормализованные числа 0,10111×2–1 и 0,11011×210.
Разность порядков слагаемых здесь равна трем, поэтому перед сложением мантисса первого числа сдвигается на три разряда вправо.
Пример. Выполнить вычитание двоичных нормализованных чисел 0,10101×210 и 0,11101×21
Разность порядков уменьшаемого и вычитаемого здесь равна единице, поэтому перед вычитанием мантисса второго числа сдвигается на один разряд вправо
Результат получился не нормализованным, поэтому его мантисса сдвигается влево на два разряда с соответствующим уменьшением порядка на две единицы: 0,1101×20.
При умножении двух нормализованных чисел их порядки складываются, а мантиссы перемножаются.
Пример. Выполнить умножение двоичных нормализованных чисел:
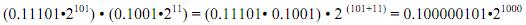
При делении двух нормализованных чисел из порядка делимого вычитается порядок делителя, а мантисса делимого делится на мантиссу делителя. Затем в случае необходимости полученный результат нормализуется.
Пример. Выполнить деление двоичных нормализованных чисел:
Использование представления чисел с плавающей точкой существенно усложняет схему арифметико-логического устройства.
Основные понятия алгебры логики. Элементарные логические операции
Как было отмечено ранее, информатика - прикладная наука, находящаяся на стыке многих наук. Вместе с тем она опирается на спектр разделов такой фундаментальной науки» как математика. Наиболее важное прикладное значение для информатики имеют булева алгебра, используемая в разработке алгоритмов программ и в синтезе цифровых устройств.
Основное понятие булевой алгебры — выказывание. Под простым высказыванием понимается повествовательное предложение, о котором можно сказать, истинно оно или ложно (третьего не дано). Высказывания обозначаются латинскими буквами и могут принимать одно из двух значений: ЛОЖЬ (обозначим 0) или ИСТИНА (обозначим 1). Например, содержание высказывания А: «дважды два равно четырем» истинно А = 1, а высказывание В: «три больше пяти» всегда есть ЛОЖЬ.
Два высказывания А и В называются равносильными, если они имеют одинаковые значения истинности, записывается А = В.
Сложное высказывание можно построить из простых с помощью логических операции: отрицания, конъюнкции, дизъюнкции, импликации и логических выражений, представляющих собой комбинации логических операций.
Операцией отрицания А называют высказывание 
(говорят «не А»), которое истинно тогда, когда А ложно, и ложно тогда, когда А истинно. Например, если событие А состоит в том, что «завтра будет снег», то А «завтра НЕ будет снега», истинность одного утверждения автоматически означает ложность второго. Отрицание - унарная (т.е. для одного операнда) логическая операция. Ей соответствует языковая конструкция, использующая частицу НЕ.
Это правило можно записать в виде следующей таблицы:
| А |
|
Такая таблица называется таблицей истинности.
Конъюнкцией (логическим умножением) двух высказываний А и В является новое высказывание С, которое истинно только тогда, когда истинны оба высказывания, записывается С = А Ù В или С = А & В (при этом говорят «С равно А и В»). Примером такой операции может быть следующая: пусть высказывание А состоит в том, что «высота шкафа меньше высоты двери», событие В «ширина шкафа меньше ширины двери», событие С «шкаф можно внести в дверь, сели ширина шкафа меньше ширины двери И высота шкафа меньше высоты двери», т.е. данная операция применяется, если два высказывания связываются союзом И.
Таблица истинности этой операции, как следует из определения, имеет вид
| А | В | А & В |
Дизъюнкцией (логическим сложением) двух высказываний А и В является новое высказывание С, которое истинно, если истинно хотя бы одно высказывание. Записывается С = A Ú В (при этом говорят: «С равно А ИЛИ В). Пример такой операции следующий: пусть высказывание А состоит в том, что «студент может добираться домой на автобусе», событие В «студент может добираться домой на троллейбусе», событие С «студент добрался домой на автобусе ИЛИ троллейбусе», т.е. данная операция применятся, если два высказывания связываются союзом ИЛИ.
Таблица истинности такой операции следующая:
| А | В | A Ú В |
Импликацией двух высказываний А (А называется посылкой) и В (В называется заключением) является новое высказывание С, которое ложно только тогда, когда посылка истинна, а заключение ложно, записывается С = А ® В (при этом говорят: «из А следует В»). Примером такой операции может быть любое рассуждение типа: если произошло событие А, то произойдет событие В, «если идет дождь, то на небе тучи». Очевидно, операция не симметрична, т.е. из В ® А не всегда истинно, в нашем примере «если на небе тучи, то идет дождь» не всегда истинно.
Таблица истинности импликации следующая:
| А | В | А ® В |
Импликация имеет следующие свойства:
А ® В ≠ В ® А
А ® А = 1
0 ® А = 1
1 ® А = А
А ® 1 = 1
А ® 0 =
Эквиваленцией двух высказываний А и В является новое высказывание С, которое истинно только тогда, когда оба высказывания имеют одинаковые значения истинности, записывается С = А «В (.С = А º В). Примером такой операции может быть любое высказывание типа: событие А равносильно событию В.
Таблица истинности:
| А | В | А «В |
Эквиваленция имеет следующие свойства:
А «В = В «А
А «В = 
«
А «1 = А
А «0 =
С помощью логических операций из простых высказываний (логических переменных и констант) можно построить логические выражения, которые также называются булевскими функциями. Например, С = (( Ú В) ® В) Ú А.
Чтобы избежать большой количества скобок в булевских функциях, принято следующее соглашение о старшинстве операций. Первыми выполняются операции и скобках, затем операции в следующем порядке: отрицание, конъюнкция и дизъюнкция слева направо, импликация, эквиваленция.
Операции не являются независимыми; одни из них могут быть выражены через другие. Можно доказать с помощью таблиц истинности следующие равносильности:
Одну и ту же зависимость между логическими переменными можно выразить различными формулами. Поэтому важно иметь возможность приводить формулы с помощью эквивалентных преобразований к некоторому стандартному виду. Существует несколько стандартных форм, к которым приводятся логические выражения с помощью эквивалентных преобразований (формулы 1 - 23).
Первая из них – дизъюнктивная нормальная форма (ДНФ), имеет вид
A1 Ú А2 Ú … Ú Аn,
где каждое из составляющих высказываний есть конъюнкция простых высказываний и их отрицаний, например: В = (
& А2 & A3) Ú (А4 & А5).
Вторая – конъюнктивная нормальная форма (КНФ), имеет вид
A1 Ù А2 Ù … Ù Аn,
где каждое из составляющих есть дизъюнкция Гфостых высказываний и их отрицаний, например: В = ( Ú А2 Ú 
) & (А4 Ú А5) & А6.
Задать булевскую функцию можно, определяя ее значения для всех наборов значений аргументов. Каждый аргумент может иметь два значения: 0 и 1, следовательно, n аргументов могут принимать 2n различных наборов. Пусть, например, булевская функция имеет три аргумента: Х1, X2, Х3. Общее число наборов 23 = 8. Зададим таблицу истинности функции, указав для каждого набора значение функции.
В комбинациях, где функция принимает значение 1, единица заменяется именем функции, а нуль — именем с отрицанием (т.е. комбинации 0 0 1 ставиться в соответствие выражение 
& 
&X3), все элементы соединяются знаками дизъюнкции.
Для рассматриваемого примера получим
F(X1, Х2, X3) = ( & &X3)Ú( & Х2 & X3)Ú(Х1 & &X3) Ú(Х1&Х2&X3).
Как нетрудно заметить, построенная функция удовлетворяет заданной таблице истинности. Функция представляет дизъюнктивную нормальную форму. Кроме того, в каждую группу дизъюнкций входят все аргументы функции. Такая ДНФ называется совершенной, а каждая группа дизъюнкций называется коституентой единицы.
Аналогично, для комбинаций, где функция принимает значение нуля, можно построить алгебраическую форму
F(X1, Х2, X3) = (Х1ÚХ2ÚX3) & (Х1Ú ÚX3) & ( ÚХ2ÚX3) & ( Ú ÚX3),
которая также удовлетворяет заданной таблице истинности и представляет собой конъюнктивою нормальную форму, в данном случае совершенную. Каждая конъюнкция называется конституентой нуля.
