IF логическое_условие GOTO метка_оператора

Здесь, если заданное условие истинно, выполняется указанный оператор (в первом случае), или производится переход к оператору с указанной меткой (во втором). Если условие ложно, выполняется оператор, следующий непос­редственно за оператором IF. Например, оператор

IF a^2>=b–2 GOTO 40

¯ нет

читается: “Если A2>=B–2, то идти к оператору 40, если нет – к оператору, записанному ниже (непосредственно под оператором IF)”. А

IF x>z THEN?Y читается:

¯ нет

“Если X>Z, тогда напечатать Y, иначе идти к следующему оператору”.

После фразы THEN (тогда) может быть использовано ключевое слово ELSE (иначе):

üIF логическое_условие THEN оператор ELSE оператор

Здесь, если условие истинно, выполняется оператор, следующий после слова THEN, иначе оператор, следующий после слова ELSE.

Например, оператор

IF a>b THEN?”А больше В” ELSE?”В больше А”

 

выводит сообщение о фактическом соотношении переменных А, В.

Другой пример. На практике иногда приходится выяснять, четное число (например Х) или нечетное. Это можно сделать с помощью следующего выражения

IF FIX(x/2)=x/2 THEN ”X – четное” ELSE ” X – нечетное ”

¶СТРУКТУРНЫЙ ОПЕРАТОР УСЛОВНОГО ПЕРЕХОДА

Здесь уместно напомнить, что всюду, где в синтаксисе команд встречается слово оператор, может быть записано несколько операторов, разделенных двоеточием. Однако этого может оказаться недостаточно – внутрь выражений THEN/ELSE может потребоваться включить много действий и даже целые процессы. В этом случае используется структурный оператор условного перехода. Такой оператор условного перехода позволяет формировать условия, влияющие на любое число строк программы.

Вид оператора:

üIF логическое_условие THEN

Операторы1

[ELSE

операторы2]

END IF

Здесь если логическое условие истинно, выполняются операторы группы 1, если нет – операторы группы 2. Присутствие фразы ELSE и следующей за ней группы операторов необязательно.

Для примера используем предыдущую задачу о сравнениичисел А и В.

IF a>b THEN

?”А больше В”

ELSE

?”В больше А”

END IF

Замечание к нотации. Для придания более наглядного вида программе удобно использовать отступы при вводе “подчиненных” операторов в структурах IF, FOR и других, как показано выше. В данном случае подчиненными операторами по отношению к структуре IF являются операторы печати.

¶ОПЕРАТОР ВЫБОРА (селектор). Оператор выбора позволяет осуществлять удобный выбор среди нескольких возможных альтернатив.

Вид оператора:

üSELECT CASE выражение_для_проверки

[CASE список_выражений_1

операторы 1]

[CASE список_выражений_2

операторы2]

...

[CASE ELSE

операторы_N]

END SELECT

где: выражение для проверки – числовое или символьное выражение;

список выражений – одно или более выражений такого же типа, что и выражение для проверки.

Если выражение для проверки совпадает с каким-либо элементом из списка выражений, приведенного после ключевого слова CASE, товыполняется группа операторов, следующих за этим словом до следующего CASE или END SELECT. Затем осуществляется переход к оператору, идущему после END SELECT. Если нет ни одного совпадения, выполняются операторы, следующие после слова CASE ELSE (если есть).

Элементы списка выражений должны иметь одну из следующих форм:

выражение_1 [,выражение_2] – проверяется совпадение выражения для проверки с любым выражением из перечисленного списка.

выражение_1 TO выражение_2 – проверяется нахождение выра­жения для проверки в диапазоне от выражения 1 до выра­жения 2.

IS логическое_условие – проверяет истинность логического условия. Условие должно начинаться с одного из знаков отношений (<, >, <=, >=, <>, =).

Пример. Здесь проверяется, при­надлежит ли переменная Х подмножеству чисел 1,3,5,7, или оно находится в диапазоне от 10 до 20, или оно больше 100 с выдачей соответствующего сообщения. Если ни одно из условий не выполняется, выдается сообщение "Остальные числа". Решение ниже слева.

Допускается соединение списков выражений любого типа. Положим, что нам нужно выяснить только факт принадлежности/непринадлежности к указанному множеству. В этом случае решение задачи (ниже справа) упрощается.

SELECT CASE x CASE 1,3,5,7 ? "x=1, 3, 5, 7" CASE 10 TO 20 ? "10<=x<=20" CASE IS > 100 ? "x>100" CASE ELSE ?"Остальные числа" END SELECT

SELECT CASE x CASE 1,3,5,7,10 TO 20, IS > 100 ? "x=1,3,5,7 или 10<=x<=20 или х>100" CASE ELSE ? "Остальные числа" END SELECT

¶ОПЕРАТОР ЗАВЕРШЕНИЯ. Оператор END (“конец”) завершает выполнение программы. Он может находиться в любом месте программы. Таких операторов может быть несколько в случае, если предполагается завершение программы не только в ее конце. Присутствие END в конце программы необязательно, поскольку после выполнения последнего оператора, она все равно заканчивается.

¶КОММЕНТАРИИ. Написанная программа спустя некоторое время даже автору кажется малопонятным набором символов. Для облегчения понимания программы в нее вставляются комментарии – тексты, поясняющие суть процессов и не влияющие на ее исполнение. Такие тексты должны начинаться со слова-оператора

üREM текст_комментария

Оператор REM может находиться как в отдельной строке, так и после любого оператора. Более удобной формой является использование для тех же целей апострофа. Ниже (слева и справа) изображены идентичные примеры комментариев.

PRINT x REM комментарии PRINT x 'комментарии

REM и это комментарии 'и это комментарии

Очевидно, что удобнее пользоваться апострофами.

¶В заключение еще один полезный оператор. Оператор очистки экрана.

üCLS

В символьном режиме курсор будет установлен в левый верхний угол, в графическом – в центр экрана.

Блок-схема. При разработке алгоритма программы сначала удобно построить его графическое представление – блок-схему. В блок-схеме отдельные операции или группы операций помещаются в прямоугольные блоки. Операции анализа (операторы IF) отображаются ромбами, имеющими два выхода. Выход ДА, соответствует истинному значению, анализируемого условия, НЕТ – ложному.

Обычно, блок-схемы обрамляют блоки НАЧАЛО и КОНЕЦ. Мы будем изображать последние только в случае, если возможно разночтение.

Организация ветвлений

Очень распространенной задачей является программирование процессов с несколькими исходами – ветвящихся процессов.

Задача 1. Для произвольного аргумента Х вычислить значение кусочно-ломаной функции Y(X) (рис. 2.3.1).

 

5+X при Х<0

Y =5 при 0<=Х<10

10–0,5X при X>=10

 

 

Одно из возможных решений задачи приведено на рис.2.3.2 и 2.3.3. Здесь имена переменных отображены строчными буквами, а ключевые слова – прописными только для наглядности. Как уже указывалось, регистр букв безразличен – в Бейсике они воспринимаются одинаково.

 

Здесь используется помеченный оператор (2 PRINT y). Необходимость в этом возникла вследствие потребности перейти к печати от операторов IF, минуя оператор y=10-0.5*x. В данном случае метка может быть любым числом, а не только 2. Замечание. В блок-схеме на связях имеющих очевидное направление стрелки можно не указывать.

Следует отметить, что практически любая задача может быть запрограммирована различными способами. Например, здесь возможно и такое решение.

INPUT x

IF x<0 THEN y=5+x: PRINT y: END

IF x<10 THEN y=5: PRINT y: END

y=10-0.5*x: PRINT y

Задача 2. Даны три произвольных числа А, В, С. Составить программу, которая анализирует их и, если сумма первых двух чисел не меньше третьего, а второе число больше первого – выдает сообщение ВЕРНО. Если хотя бы одно из условий не выполняется – то сообщение НЕВЕРНО. Иными словами

“ВЕРНО” если А+В>=C и В>A

“НЕВЕРНО” – в противном случае

На рис. 2.3.4 и 2.3.5 представлено решение (блок-схема и программа), полностью адекватное условию. Однако в некоторых случаях решение удобно искать, преобразовав условие на обратное, т.е.

“НЕВЕРНО” если А+В<C или В<=A

“ВЕРНО” – в противном случае

Это позволяет иногда упростить программирование. Программа для этого случая приведена на рис. 2.3.6.

Программы к задаче 2.

INPUT a,b,c INPUT a,b,c

IF a+b>=c GOTO 7 IF a+b<c GOTO 15

? “Неверно”: END IF b<=a GOTO 15

7 IF b>a THEN? “Верно”? “Верно”: END

15? “Неверно”

Рис. 2.3.5 Рис. 2.3.6

¶ЛОГИЧЕСКИЕ ФУНКЦИИ. При необходимости выполнять анализ одновременно нескольких условий удобно воспользоваться логическими функциями. Аргументами логических функций являются высказывания, в отношении которых всегда можно сказать истинны они или ложны. К таким высказываниям относятся математические операции сравнения – равно, больше, меньше и т.д. Так, например, выражение вида Х=Y всегда может быть только истинным или только ложным. Программисту доступны следующие шесть логических операций (таблица 2.3.1):

 

Функция	Название	Определение
NOT	Отрицание НЕ	Выражение NOT A истинно тогда и только тогда, когда А ложно
AND	Логическое умножение И	A AND B истинно тогда и только тогда, когда истинно и А и истинно В
OR	Логическое сложение ИЛИ	A OR B истинно тогда и только тогда, когда хотя бы одно из А и В истинно
XOR	Исключающее ИЛИ	A XOR B истинно тогда и только тогда, когда значения аргументов не совпадают
EQV	Эквивален- тность	A EQV B истинно тогда и только тогда, когда оба аргументы истинны или оба ложны
IMP	Импликация	A IMP B принимает значение ложь, если А истинно, а В ложно, и истина в других случаях

Таблица 2.3.1

Важнейшими для нас являются функции И, ИЛИ, НЕ, которые образует так называемый основной полный набор логических функций, т.е. только с их помощью (без привлечения других элементарных логических функций) можно описать какие угодно сложные логические зависимости. Остановимся на них подробнее. Функция НЕ (NOT) – является функцией одного аргумента. Другие названия функции НЕ – функция инверсии, поскольку ее значение всегда обратно аргументу. Поведение функции описывает таблица 2.3.2. Например, следующие два оператора полностью идентичны

IF X<10 THEN Y=5 IF NOT X>=10 THEN Y=5

Поведение логических функций И, ИЛИ описывает таблица 2.3.3. Эти функции требуют двух аргументов. Функция И (AND) истинна тогда и только тогда, когда истинны все ее аргументы. Функция ИЛИ (OR) истинна тогда, когда истинен хотя бы один из ее аргументов. Если нет скобок, функции вычисляются в следующей последовательности: НЕ, И, ИЛИ.

В качестве примера снова рассмотрим задачу 2 в исходной формулировке. Теперь ее решение сводится практически к одной строке и приведено ниже.

INPUT a,b,c

IF a+b>=c AND b^2>a THEN? “Верно” ELSE? “Неверно”

 

Аргумент	Функция НЕ		Первый аргумент	Второй аргумент	Функция И	Функция ИЛИ
Ложь	Истина		Ложь	Ложь	Ложь	Ложь
Истина	Ложь		Ложь	Истина	Ложь	Истина
			Истина	Ложь	Ложь	Истина
		Истина	Истина	Истина	Истина
Таблица 2.3.2			Таблица	2.3.3

Другой пример. Для произвольных чисел А, В, С выяснить, правда ли что первое число самое большое, а последнее – самое маленькое.

IF a>b AND a>c AND c<a AND c<b

THEN? “Верно” ELSE? “Неверно”

Еще. Правда ли, что среди чисел А, В, С имеется ровно одна единица.

IF (a=1 AND b<>1 AND c<>1) OR

(a<>1 AND b=1 AND c<>1) OR

(a<>1 AND b<>1 AND c=1)

THEN? “Верно” ELSE? “Неверно”

Здесь скобки введены только для наглядности поскольку операция AND все равно выполняется прежде операции OR.

& Тест. 2.3.1. Укажите результат, выдаваемый программой 1). 1, 2) 2.

x=2: y=4: z=3

if x>y or y>z then print 1 else print 2

@ Контрольная задача. В устройстве ввода ЭВМ подготовлено четыре произвольных числа: A,B,C,D. ЭВМ должна ответить на вопрос: Правда ли что...? (вопрос берется из таблицы). Ответ ЭВМ должна вывести в виде текста: слова ”Правда” или ”Неправда”. Составить блок-схему, программы. Сделать проверку для произвольных аргументов.

Вопрос

Все числа положительны?

Ни одно из чисел не превышает число 90?

Каждое из первых двух чисел больше каждого из последних двух?

Первое число меньше остальных?

Эти числа расположены в возрастающей последовательности?

Эти числа расположены в убывающей последовательности?

Среди этих чисел есть равные?

Среди этих чисел нет равных?

Первое число не самое маленькое?

Все четыре числа равны между собой?

Организация циклов

В простых примерах, рассмотренных выше, вообще говоря, не требо­валось привлечения ЭВМ и программирования. Все они достаточно быстро могли быть решены вручную или с помощью калькулятора. Сила ЭВМ заключается в возможности простыми средствами осуществлять многократное повторение заданных действий – циклов.

¶ИТЕРАЦИОННЫЕ ЦИКЛЫ. В случае, если количество циклов, необходимых для решения задачи, заранее неизвестно, такие циклы называются итерационными. Рассмотрим ряд примеров.

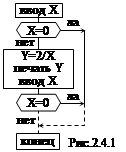
Задача 3. Пусть для некоторого множества чисел Х нужно вычислить и отпечатать функцию 2/Х. Ввод и вычисления следует прекратить после обнаружения первого Х, равного нулю (деление на ноль невозможно).

		Программа к задаче 3 3 INPUT x IF x=0 GOTO 9 y=2/x PRINT x y GO TO 3 9 END

 

Очевидна следующая блок-схема (рис. 2.4.1). Блоков ввода, вычисления, печати и анализа столько, сколько чисел в последовательности до первого нуля. Чисел может быть очень много и подобный подход, конечно, неприемлем, не говоря уже о том, что и количество их заранее неизвестно. Такие программы строятся по-иному. Обрабатывающая часть программы записывается только раз, но охватывается петлей возврата (рис. 2.4.2). Тогда одни и те же операторы будут выполняться многократно до тех пор, пока Х¹0.

Задача 4. Пусть для аргумента Х, находящегося в диапазоне от 3 до 9, требуется вычислить и напечатать значение функции Y=(X–6)2, где Х изменяется с шагом 2 (рис. 2.4.3). Блок-схема алгоритма изображена на рис. 2.4.4.

Справа от текста программы сделаны выкладки по проверке решения. В каждой строке вручную вычисляется и указывается значение соответствующей переменной. Выкладки по проверке выполняются сверху-вниз, слева-направо по ходу исполнения программы. Стрелки показывают связи между циклами. Видим, что заданная последовательность изменения Х (3, 5, 7,...) наблюдается и последнее значение Y вычисляется для Х=9. При следующем приращении Х оно становится равным 11 и пятый цикл не выполняется, поскольку при Х>9 программа завершается.

Здесь следует отметить, что нет никакого технически простого способа предварительной проверки правильности написанных программ. Для этой цели программисту приходится вручную по тексту программы рассчитывать значения всех переменных и сличать их с желаемыми (известными из условия). Конечно, проверка выполняется не для всей задачи, а только для небольшого числа (например, трех) начальных циклов и при этом тщательно анализируется значение условия выхода из цикла (оператор IF).

 

 

@ Контрольная задача. Пусть дана функция Y=10–2X. ЭВМ должна вычислить и напечатать значения этой функции для последовательных значений Х: 0, 0.5, 1, 1.5, 2, 2.5,... и т.д. до тех пор, пока Y не станет отрицательным.

 

Программа	Проверка
к задаче 4	1 цикл	2 цикл	3 цикл	4 цикл
x=3 2 IF x>9 GOTO 4 y=(x–6)^2 ? x,y x=x+2 GOTO 2 4 END	x=3 x=3<9 y=9 3,9 x=3+2=5	5<9 y=1 5,1 x=7	7<9 y=1 7,1 x=9	9=9 y=9 9,9 x=11	11>9 конец

¶АРИФМЕТИЧЕСКИЕ ЦИКЛЫ. Если число повторений известно заранее – такие циклы называются арифметическими.

Задача 5. Пусть в условиях предыдущей задачи 4 не известно предельное значение аргумента, но зато задано количество точек аргумента – 4. Поскольку в данном случае не задано последнее значение Х, признак окончания циклов придется формировать самим. Для этого вводится переменная, которая фиксирует число уже выполненных циклов, т.е. счетчик циклов (назовем ее I). В исходном состоянии (рис. 2.4.5) берем его равным 1.

Программа	Проверка
к задаче 5	1 цикл	2 цикл	3 цикл	4 цикл
x=3: i=1 8 IF i>4 GOTO 2 y=(x–6)^2 ? x y x=x+2 i=i+1 GO TO 8 2 END	x=3, i=1 i=1<4 y=9 3, 9 x=5 i=2	2<4 y=1 5, 1 x=7	3<4 y=1 7, 1 x=9	4=4 y=9 9, 9 x=11	5>4 конец

После выполнения очередного цикла счетчик получает приращение, увеличиваясь на единицу (I=I+1). В начале каждого цикла в операторе IF делается проверка на достижение счетчиком последнего разрешенного значения (у нас 4). Если I<=4 программа продолжает вычисление функции, если нет (I>4) – счет прекращается. Ниже приведена программа и выкладки по ее проверке. Как видим, результат проверки совпал с результатом, полученным ранее. Исходное значение счетчика циклов и его приращения могут выглядеть по-разному. Главное, чтобы было выполнено заданное число циклов. В нашем примере был использован счетчик на возрастание I=1,2,3,... до N (N – число шагов). Можно начинать счетчик с нуля: I=0,1,2,... до N-1. Возможен счетчик на убывание: I=N–1,... 3,2,1 до 0 и т.д. Обычно, если нет оснований для другого, используется счетчик на возрастание с шагом единица от 1 до N.

¶ЗАДАЧИ НА НАКОПЛЕНИЕ. В практике очень распространены задачи на накопление, т.е. на нахождение сумм и произведений последовательности переменных. Такие задачи могут встречаться как в формулировке итерационных, так и арифметических циклов.

Задача 6. Пусть требуется найти сумму N произвольных чисел Х. Блок-схема алгоритма приведена на рис. 2.4.6, а программа ниже. Здесь сумма накапливается в переменной S с помощью оператора S=S+X. Начальное значение суммы берется равным нулю (S=0).

Программа	Проверка для N=3 X=2,4,3
к задаче 6	1 цикл	2 цикл	3 цикл
INPUT “N=”,n i=1: s=0 3 IF i>n GOTO 8 INPUT “X=”,x s=s+x i=i+1 GOTO 3 8 PRINT s	n=3 i=1, s=0 1<3 x=2 s=2 i=2	2<3	3=3	4>3 s=9

¶ЧИСЛОВЫЕ РЯДЫ. Типичной циклической задачей на накопление является вычисление числовых рядов.

Задача 7. Пусть требуется найти сумму S для N членов геометрической прогрессии вида

A1 A2 A3 A4 N

S = 3 + 6 + 12 + 24 +... + = åАI

S1 S2 S3 S4

Здесь каждый следующий член прогрессии АIравен предыдущему AI–1, умноженному на два. Если учесть введенные обозначения, можно записать так называемые рекуррентные формулы

SI= SI–1 + AI, где S0= 0

AI= 2AI–1 A1= 3

Или, как принято в программировании

S=0, S=S+A

A=3, A=2A

Аналогично строятся программы для циклического произведения, однако исходное значение искомого произведения берется равным единице. Если действовать по аналогии с суммой и сделать его равным нулю, результат всегда будет также нулем, поскольку умножение на нуль дает только нуль.

 

Программа		Проверка	для N=3
к задаче 7	1 цикл	2 цикл	3 цикл	4 цикл
INPUT n	n=3
a=3: i=1: s=0	a=3, i=1,s=0
3 IF i>n GOTO 9	i=1<3	2<3	3=3	4>3
s=s+a	s=0+3=3	3+6=9	9+12=21
a=2*a	a=2*3=6
i=i+1	i=1+1=2
GOTO 3
9? s				s=21

@ Контрольная задача. Составить программу вычисления и выдачи на печать суммы N элементов числового ряда.

№	Вариант	№	Вариант
	y=1+4+7+10+13+...		y=–56–54–52–50–48–...
	y=2+4+8+16+32+...		y=18+20+22+24+26+...
	y=60+53+46+39+32+...		y=85+80+75+70+65+...
	y=–4–8–16–32–64–...		y=–42–40–38–36–34–...
	y=2+6+18+54+162+...		y=–20–15–10–5–0+5+...

¶ОПЕРАТОР АРИФМЕТИЧЕСКОГО ЦИКЛА

Принципы построения программ с арифметическими циклами можно проиллюстрировать обобщенной блок-схемой на рисунке 2.4.7.

 

Группа операторов внутри цикла называется телом цикла. Только обрабатывающая часть цикла полезна. Остальные операторы являются обслуживающими, необходимыми для организации цикла. Этот механизм в алгоритмических языках обычно реализует специальный оператор цикла, который мы сейчас рассмотрим. Его применение упрощает программирование и снижает возможность совершения ошибок.

Структура вида:

 

ü

FOR

изменяемая переменная

=

начальное значение

TO

конечное значение

STEP шаг

Операторы

NEXT

последовательно выполняет операторы, находящиеся между оператором FOR до оператора NEXT столько раз, сколько нужно для того, чтобы изменяемая переменная от начального значения достигла конечного значения с установленным шагом.

Например:

FOR a = 3 TO 7.5 STEP 0.8

Операторы

NEXT a

Здесь группа операторов от оператора FOR до оператора NEXT будет повторяться столько раз, сколько нужно, чтобы переменная А, изменяясь с шагом 0.8 от значения равного 3, достигла 7.5. Таким образом: A=3; 3.8; 4.6; 5.4; 6.2; 7, т.е. цикл будет выполнен 6 раз.

В качестве параметров оператора цикла разрешены выражения. Например: FOR c=b+2 TO k STEP x–2. Если шаг изменения переменной цикла 1, разрешается его не указывать. Так, операторы

FOR i=4 TO k STEP 1 и FOR i=4 TO k

полностью эквивалентны. Дословно такой оператор интерпретируется следующим образом: “Выполнять операторы цикла от оператора FOR до оператора NEXT столько раз, сколько нужно, чтобы переменная I, изменяясь с шагом 1, достигла значения k.” Цикл завершается в момент, когда переменная цикла становится больше предельного значения цикла (k).

Допускается отрицательный шаг и превышение начального значения цикла над конечным, например

FOR i=20 TO 10 STEP -3

Здесь переменная I последовательно получит значения: 20, 17, 14, 11.

После слова NEXT обычно, но необязательно, указывается имя изменяемой переменной цикла (переменной, следующей непосредственно после слова FOR), что позволяет легко контролировать правильное закрытие циклов. Для простых циклов имя переменной можно не указывать.

Оператор цикла является сильнейшим средством программиста. Он один заменяет несколько операторов в цикле, построенном обычным образом – это операторы задания исходного значения циклической переменной (или счетчика циклов) и операторы ее приращения и анализа. Оператор FOR удобен как для реализации программ с арифметическими циклами, так, во многих случаях, и для программ с итерационными циклами.

На блок-схемах оператор FOR отображается в виде фигуры “прямоу­гольник в ромбе”, которая имеет два выхода. Выход ДА соответствует случаю, когда переменная цикла меньше или равна своему предельному значению – цикл продолжает выполняться. Выход НЕТ – случаю превышения переменной этой границы – цикл завершается. Иногда можно воспользоваться упрощенным обозначением цикла FOR, когда он включается в виде заголовка в прямоугольник, содержащий операторы цикла. К такой форме возможно прибегать, если тело цикла не содержит разветвлений или собственных циклов.

 

 

Решим задачу 7 с применением оператора FOR. Здесь необходимо просум­мировать в переменную S все числа Х из множества N чисел. Блок-схема приведена на рис. 2.4.8 в обоих возможных вариантах. Как видим, второй гораздо более компактен, однако, как уже говорилось, он возможен не всегда.

 

Программа	Проверка для N=3
к задаче 7	1 цикл	2 цикл	3 цикл
INPUT n a=3: s=0 FOR i=1 TO n s=s+a a=2*a NEXT PRINT s	n=3 a=3, s=0 i=1<3 s=0+3=3 a=2*3=6	2<3	3=3	4>3 s=21

Если необходимо выйти из цикла FOR до его естественного завершения (до выполнения всех циклов), можно применить оператор GOTO, но удобнее воспользоваться специальным оператором выхода вида

üEXIT FOR

который передает управление на оператор, следующий непосредственно за оператором NEXT.

Если нужно, не выполняя до конца текущего цикла, начать следующий, следует перейти оператором GOTO непосредственно на оператор NEXT. В задаче 8, например, это оператор IF x<0 THEN s=s+x: GOTO 9

& Тест. 2.4.1. Чему будет равно h после завершения программы? 1). 5.8, 2). 6, 3).6.1.

h=0: k=2: m=7

for i=k*2 to m-1 step 0.5

h=h+1

next

	Проверка для N=5
Программа к задаче 8	цикл	цикл	цикл	цикл	цикл
INPUT n kp=0: s=0: p=1 FOR i=1 TO n INPUT x IF x=0 GOTO 7 IF x<0 THEN s=s+x: GOTO 9 kp=kp+1 p=p*x 9 NEXT ?“Нулей нет” 7? s p kp	n=4 i=1<5 x=3 x≠0 x>0 kp=1 p=3	2<5 x=-2 x≠0 x<0, s=-2	3<5 x=1 x≠0 x>0 kp=2 p=3	4<5 x=-3 x≠0 x<0, s=-5	5=5 x=2 x≠0 x>0 kp=3 нулей нет p=6	6>5 -5,6,3

Задача 8. Для N произвольных чисел Х вычислить и отпечатать: сумму отрицательных чисел S, количество положительных чисел КР, произведение положительных чисел Р. Все вычисления производить до появления первого нуля в последовательности. Если нуль не встретился, кроме S, KP и Р напечатать сообщение НУЛЕЙ НЕТ. Блок-схема алгоритма приведена на рис. 2.4.9. В программе сделана проверка для N=5 и Х=3,–2,1,–3,2. В результате получено S=–5, P=6, KP=3.

@ Контрольная задача. Имеется N произвольных чисел Х. Составить программу вычисления и напечатать сумму всех положительных чисел S, число отрицательных чисел К и произведение всех чисел, не равных нулю P. Сделать проверочные выкладки для N=5 (аналогичные выполненным выше). В качестве значений Х использовать последовательные цифры натурального ряда с изменяющимися знаками (Х=0, –1, 2, –3, 4, –5).

Задача 9. Для чисел Х и Y найти наибольший общий делитель. Нахождение НОД будем выполнять путем последовательного перебора сверху вниз всех натуральных чисел от максимального из X и Y до 1. Наименьшим делителем считаем первое значение i, которое делит оба числа без остатка.

Программа к задаче 9

INPUT "Введите числа X и Y", x, y

x = 12: y = 8

IF x<y THEN k=x ELSE k=y ‘определение минимального из X и Y – K

FOR i = k TO 1 STEP -1 ‘последовательный перебор чисел от К до 1

‘если Х и Y делятся нацело, делитель (i) найден

IF x MOD i=0 AND y MOD i=0 THEN PRINT "НОД="; i: EXIT FOR

NEXT

END

@ Контрольная задача. Имеется N произвольных чисел, среди которых есть положительные, отрицательные и равные нулю. Составить программу, выполняющую задачу из следующей таблицы (варианты выберите сами).

 

Задача

Вычислить сумму всех положительных чисел

Вычислить количество чисел, квадрат которых меньше 10

Вычислить количество положительных, количество нулевых чисел и сумму отрицательных

Ответить на вопрос: правда ли, что среди этих чисел имеются отрицательные (ответ должен быть в виде текста “ДА” или “НЕТ”)

Напечатать все числа из очереди, квадрат которых превышает 7

Вычислить произведение положительных чисел

Подсчитать число четных и сумму нечетных чисел.

Суммировать числа до тех пор, пока случайно не встретится число 2. Напечатать получившуюся сумму. Если двойка не встретилась, напечатать текст “Числа слишком малы”.

Суммировать квадраты чисел до тех пор, пока сумма квадратов не превысит 40. Напечатать, на котором по счету числе произошло это событие. Если оно не произошло вообще, напечатать текст “Числа слишком малы”

Определить и напечатать, каким по счету в очереди стоит число 3. Если троек несколько, нас интересует только первая из них. Если троек нет совсем, напечатать сообщение “Троек нет”.

@ Контрольная задача. В банке хранится известное количество (N) срочных вкладов. О каждом вкладе известно его значение на начало года – X. Размер прибыли зависит от величины вклада. Если вклад до 10000 руб. – прирост составляет 10% годовых, если до 50000 руб. – 12%, если больше – 15%. Вычислить и напечатать значение каждого вклада на конец года, а также суммарные вклады на начало и конец года. Задачу решить двумя способами – с оператором цикла и без него. Указание. Процент увеличения вклада удобно отобразить в виде коэффициента. Так при 12% годовых, значение вклада на конец года соответствует 1.2X.

¶ОПЕРАТОР ИТЕРАЦИОННОГО ЦИКЛА имеет вид

üWHILE условие

Операторы

WEND

Такая конструкция позволяет легко организовывать итерационные циклы – операторы, входящие в тело цикла выполняются до тех пор, пока истинно условие.

Для примера снова решим задачу 3 (вычислять и печатать Y=Х2до обнаружения первого Х=0). Программа приведена справа.

INPUT x

WHILE x<>0

?х; х^2

INPUT x

WEND

Если параметр WHILE условие опущен, цикл будет выполняться бесконечно. В этом случае внутри него должно быть предусмотрено средство выхода, например строка GOTO. Кроме того, в Бейсике имеется еще один оператор цикла с условием. Он имеет две разновидности: цикл с предусловием (условие рассматривается до входа в цикл)

üDO [WHILE/UNTIL условие]

Операторы

LOOP

и цикл с постусловием (условие оценивается после выполнения тела цикла)

üDO

Операторы

LOOP [WHILE/UNTIL условие]

Ключевое слово UNTIL действует обратным образом по отношению к WHILE, т.е. UNTIL-цикл будет выполняться до тех пор пока условие не станет истинным. Иными словами WHILE условие=UNTIL NOT условие.

Здесь, имеется собственный оператор принудительного выхода из цикла

üEXIT DO

Структуру с постусловием удобно применять в случае, если цикл необходимо выполнить хотя бы один раз независимо от значения условия или, если само условие формируется в цикле и не может быть оценено до входа в цикл.

& Тест. 2.4.2. Сколько раз будет выполнен цикл и чему будет равно k по завершению программы? 1). k=0, 2). k=-1, 3). k=1.

k=13

while k>0

k=k-2

wend

2.5. Работа с массивами

Как правило, данные для вычислений на компьютере задаются в упорядоченной форме – в виде последовательности (вектора) чисел или в виде таблицы (матрицы) чисел. Такие совокупности данных называются массивами. Построение программ, оперирующих с элементами массивов – важнейшая часть техники программирования.

Например, вектор А длиной К чисел и матрица В из N строк и M столбцов (всего из N*M элементов) выглядят следующим образом.

B11, B12,... B1M

A =[A1, A2, A3,... AК] B = B21, B21,... B2M

.....

BN1, BN2,... BNM

Цифры при имени массива, указывающие порядковый номер эле­мента, называются индексами. В алгоритмических языках элементы массивов АIи BIJобозначаются как А(I) и B(I,J). К массиву в целом обратиться нельзя. Обработка массива обычно означает последовательную обработку отдельных его элементов.

¶ОПЕРАТОР ОПИСАНИЯ МАССИВОВ. Если предполагается работа с массивами, предварительно следует “известить” об этом компьютер оператором вида

üDIM список_массивов

Описание массива содержит имя массива и его размерность. Например, оператор DIM A(20), B(4,6) читается как “Установить размерность одномерного массива А из 20 элементов и двумерного массива В из 24–х элементов (4 строки, 6 столбцов)”.

По умолчанию отсчет элементов в Бейсике начинается с нуля, то есть оператор DIM А(20) определяет на самом деле 21 элемент памяти (нулевой элемент можно игнорировать). Если есть необходимость установить нестандартную нумерацию, можно при определении размерности использовать указатель вида нижняя граница индекса ТО верхняя граница. Например, оператор DIM Y(5 TO 20, 1 TO 8) определяет двухмерный мас­сив Y, у которого первый индекс изменяется от 5 до 20, а второй – от 1 до 8. Размерность массива задается исходя из условий решаемой задачи.

Первоочередной задачей при работе с массивами является ввод-вывод данных в них, который организуется с помощью циклов, как, например, показано ниже.

INPUT n INPUT n,m FOR i=1 TO n

DIM a(n) DIM b(n,m) FOR i=1 TO n

FOR i=1 TO n FOR i=1 TO n PRINT b(i,j);

INPUT a(i) FOR j=1 TO m NEXT j

NEXT i INPUT b(i,j) PRINT

NEXT j NEXT i

NEXT i

Слева осуществляется ввод данных в вектор А размерностью N эле­ментов. В центре – в матрицу В размерностью N строк на M столбцов. Ввод осуществляется с помощью двух циклов, один из которых вложен в другой. В наружном цикле изменяется первый индекс I элемента матрицы В, во внутреннем – второй индекс J. Таким образом, второй индекс J изменяется быстрее, чем первый. Это означает, что ввод элементов матрицы будет производиться в следующей последовательности: B(1,1), B(1,2),..., B(1,M); B(2,1), B(2,2),..., B(2,M);...; B(1,N), B(1,N),... B(M,N), т.е. по строкам. Замечание. Два последних оператора могут быть объединены в один вида NEXT j,i (первым должен быть указан индекс внутреннего цикла, вторым – внешнего).

Аналогичным образом осуществляется и вывод (фрагмент программы справа), но вместо оператора INPUT используется оператор PRINT. Здесь, однако, следует позаботиться об удобстве восприятия выводимых данных. Желательно, чтобы строка матрицы занимала на экране именно одну строку. Для этого во внутреннем цикле печати нужно поставить точку с запятой после оператора вывода (PRINT;), что подавляет возврат каретки после вывода каждого числа. Для того, чтобы осуществить переход на новую строку после завершения предыдущей, ниже оператора NEXT j следует поставить пустой оператор PRINT, который переведет вывод на следующую строку экрана. Кроме того, для обеспечения фиксированного расположения элементов матрицы друг под другом в столбцы, имеет смысл использовать для вывода не оператор PRINT, а PRINT USING (например PRINT USING “####.##”; b(i,j);).

Задача 10. В векторе С предельной размерности 30 элементов найти максимальный по значению элемент и его номер в С. Ниже приведена программа и ее проверка для N=4 и C=[5,2,7,4] в ее обрабатывающей части (с оператора m=c(1)). Здесь переменная М запоминает значение максимального элемента, а К – номер этого элемента в векторе С. Первоначально в качестве такого элемента берется самый первый.

 

Программа к задаче 10 DIM c(30) INPUT n FOR i=1 TO n INPUT c(i) NEXT		Проверка
m=c(1): k=1 FOR i=2 TO n IF m<c(i) THEN m=c(i): k=i NEXT ?m k	m=5, k=1 i=2 5>2	i=3 5<7 m=7,k=3	i=4 7>4	i=5 7, 3

Задача 11. Определение значения вклада в банке на конец года. Положим в банке имеется N счетов вкладчиков. Для всех известны значения остатков на счете в конце каждого квартала. Следует определить и напечатать значения всех вкладов на конец года с учетом известного процента роста вклада Р. Данные о вкладах хранятся в массиве Х из N строк и пяти столбцов. Первые четыре элемента каждой i-ой строки (Х(i,1), Х(i,2), Х(i,3), Х(i,4)), хранят остатки вклада на конец каждого из четырех кварталов года. В последний, пятый элемент строки X(i,5) следует занести вычисленную величину вклада на конец года, который равен остатку вклада на конец последнего квартала Х(i,4) плюс установленный процент Р/100 от среднего значения вклада (Х(i,1)+Х(i,2)+ Х(i,3)+Х(i,4))/4 за год. Таким образом, X(i,5)=Х(i,4)+ (Р/100)*(Х(i,1)+Х(i,2)+ Х(i,3)+Х(i,4))/4.

 

I кв Х(i,1)

II кв Х(i,2)

III кв Х(i,3)

IV кв Х(i,4)

Остаток на конец года X(i,5)=Х(i,4)+(Р/100)*(Х(i,1)+Х(i,2)+Х(i,3)+Х(i,4))/4

 

Кроме перечисленного, следует найти сумму всех вкладов в банке S и среднее значение вклада, приходящееся на одного вкладчика S/N.

Программа к задаче 11

CLS

INPUT "Введите число вкладчиков и процент ",N,P

DIM x(n,5)

FOR i=1 TO n

FOR j=1 TO 4

PRINT"Введите остаток по вкладу номер" i "за" j "квартал ";

INPUT x(i,j)

NEXT j,i

s=0

PRINT" Счет Остатки по кварталам ВСЕГО"

PRINT" I II III IV"

FOR i=1 TO n

x(i,5)=х(i,4)+(р/100)*(х(i,1)+х(i,2)+х(i,3)+х(i,4))/4

PRINT USING "########"; i,x(i,1),x(i,2),x(i,3),x(i,4),x(i,5)

s=s+x(i,5)

NEXT

PRINT "Сумма всех вкладов =" s;

PRINT "Средняя величина вклада =" s/n

Задача 12. Сортировка чисел в массиве. Пусть имеется вектор чисел Х длиной N. Напечатать массив в порядке убывания значений его элементов.

Алгоритм реализуется при помощи двух вложенных циклов (рис. 2.5.1). В наружном цикле последовательно перебираются числа X(i) в массиве и во вложенном цикле сравниваются со всеми оставшимися числами справа от данного X(j). Если выясняется, что какое-то из Х(i) меньше сравниваемого, они меняются местами – большее число становится на место меньшего. В программе для упрощения в качестве элементов массива взяты их номера i. Если вектор имеет длину четыре (Х(4)), то будет выполнена следующая последовательность перестановок чисел массива: 1,2,3,4; 2,1,3,4; 3,1,2,4; 4,1,2,3; 4,3,2,1.

	Программа к задаче 12 INPUT n DIM x(n) 'формирование исходного вектора FOR i = 1 TO n: x(i) = i: NEXT FOR i = 1 TO n - 1 FOR j = i + 1 TO n 'если x(i)<x(j), числа меняются местами IF x(i)<x(j) THEN SWAP x(j), x(i) NEXT j NEXT i 'вывод результатов FOR i = 1 TO n: PRINT x(i): NEXT

Задача 13. Транспонирование матрицы. Операция транспонирования широко используется в линейной алгебре и заключается в перевороте элементов квадратной матрицы относительно главной диагонали (диагонали идущей сверху-вниз, слева-направо).

На рис. 2.5.2 приведены исходная и транспонированная матрица А размерности 6 на 6. Если внимательно приглядеться, можно заметить, что элементы массива с индексами I и J поменялись местами элементами с индексами J и I, т.е. A(I,J) « A(J,I).

Программа транспонирования изображена ниже. В качестве наполнения исходной матрицы используются ее индексы.