| Номер шага резолюции | Целевое предложение | Исходное предложение | Резольвента | |
| ?-а. | a:-b,c,d. | ?-b,c,d. | ||
| ?-b,c,d. | b:-c,f. | ?-e,f,c,d. | ||
| ?-е,f,с,d | e.?-f,c,d. | |||
| ?-f,c,d. | f.?-c.d. | |||
| ?-c,d. | c.?-d. | |||
| ?-d. | d. Пустая |
При выполнении логического вывода, если необходимо, происходит конкретизация переменных. Рассмотрим пример.
Программа 113
любит(юрий,музыку).
любит(сергей,спорт).
любит(А,книги):-читатель(А),любопытный(А).
любит(сергей,книги).
любит(сергей,кино).
читатель(юрий).
любопытный(юрий).
?- любит(X,музыку), любит(X,книги).
Двойной запрос в этой программе может быть представлен целевым деревом:
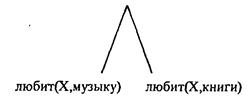
Вначале, просматривая программу сверху вниз. Пролог находит первое предложение, соответствующее первой подцели запроса:
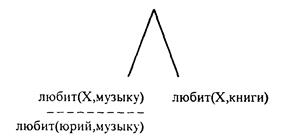
Переменная Х конкретизируется значением «юрий». Начинается согласование 2-й подцели запроса с условием Х=юрий. 1-е и 2-е предложения программы не соответствуют подцели. В 3-ем предложении:
любит(А,книги):-читатель(А), любопытный(А).
аргумент А заголовка есть переменная, поэтому она может соответствоватьX, т.е. получает значение А=юрин; вторые аргументы совпадают. Теперь тело правила образует новое множество целей для согласования. Получаем целевое дерево:


Затем Пролог будет искать факты, соответствующие новым подцелям. Последнее результирующее дерево:


Рассмотрим еще один пример.
Программа 114
любит(оля,чтение).
любит(света,бадминтон).
любит(для,бадминтон).
любит(лена,плавание).
любит(лена,чтение).
?- любит(X,чтение), любит(X,плавание).
Запрос означает: есть ли люди, которым нравится и чтение, и плавание? Сначала Пролог ищет факт, сопоставимый с первой частью вопроса: любит(Х, чтение). Подходит первый же факт программы
любит(оля,чтение).
и переменная Х связывается значением «оля». В то же время Пролог фиксирует в списке фактов указатель, показывающий состояние процедуры поиска. Далее Пролог пытается согласовать вторую часть запроса при условии Х = оля, т.е. ищет с самого начала программы факт «любит(оля, плавание)». Такого факта в программе нет, и поиск заканчивается неуспешно. Тогда Пролог возвращается к первои части запроса: любнт(Х,чтение), «развязывает» переменную Х и продолжает поиск подходящих фактов, начиная с ранее установленного в списке фактов указателя Подходит факт «любит(лена,чтение)», переменная Х конкретизируется значением «лена», и далее вторая часть вопроса успешно согласуется с фактом «любит(лена, плавание)». Пролог выполнил в данном примере поиск с возвратом.
Графически процесс выполнения программы представляется в виде обхода бинарного дерева - дерева вывода, типа изображенного на рис.3.16. Вершины дерева обозначают вопросы, а ребра показывают возможные пути вывода, причем для каждого ребра характернысвои правила и унифицирующая подстановка значений переменных.

Рис.3.16. Дерево вывода программы на Прологе
Обход дерева начинается с движения от вершины (запроса) по самой левой ветви вниз до конца (abed), при этом запоминаются все точки ветвления (точки возврата). При достижении конца ветви решение будет либо найдено, либо нет. В обоих случаях Пролог продолжает дальнейший поиск решений. Выполняется возврат в последнюю точку ветвления с. При этом конкретные значения, присвоенные переменным при движении вниз на сегменте c-d. отменяются, и движение вниз продолжается по расположенной справа ветви с-е до конца дерева вниз. Затем произойдет возврат в предыдущую точку ветвления b и движение продолжится по ветви bfg, и так до тех пор, пока все дерево вывода не будет пройдено.
РЕКУРСИЯ
Существует целый класс задач, в которых отношения между объектами можно определить, только пользуясь самими определяемыми соотношениями. Получающиеся при этом правила называются рекурсивными.
Пример: рекурсивное определение натурального числа:
1) 1- натуральное число;
2) число, на 1 большее натуральногочисла, также натуральное.
В системах логического программирования рекурсия служит также дляописанияциклов, повторений и является важнейшим методом программирования.
Рассмотрим простой пример: вычисление факториала натурального числа n (n!). Определение n! рекурсивно:
1)1!=1,
2)n!=(n-l)!*n.
Для описания отношения «факториал» междуn и n! будем использовать двухарный предикат
факт(N,М). Тогда база знаний, соединенная с запросом, приобретает вид (программа 115);
Программа 115
факт(1,1).
факт(N,Х): - факт(N-1,V), Х is Y*N.
?- факт(3,А);
В данной программе правило «факт» вызывает само себя - это и есть рекурсия. Запись is Y*N представляет собой обращение к встроенному предикату «is» («есть») для описания арифметического действия.
Процесс работы программы можно изобразить следующим образом:
?факт(3,A0).
ОТВЕТ: А=6
?факт(1,A2).
Х1= 2*3 = 6
факт(1,1)
Х2=1*2=2
Здесь стрелочка вниз означает сопоставление и резолюцию, а стрелочка вверх - возврат и завершение отложенного вычисления.
Правило «факт» вызывает само себя - происходит углубление рекурсии (прямой ход). При этом в памяти ЭВМ выделяется место для переменных А,АО,А1,А2 и N,NO,N1,N2, образующих стеки. При согласовании вопроса с предикатом факт(1,1) рекурсия прекращается и начинается возврат из рекурсии (обратный ход) - выполнение отложенных на прямом ходе согласований. Предикат факт(1,1) играет очень важную роль - это ограничитель рекурсии, условие ее завершения.
Отметим, что Пролог стремится найти все решения поставленной задачи,а значит, после появления ответа А=6 происходит возврат к вопросу?факт(1,А2) и попытке согласовать его с правилом «факт». Это приводит к бесконечному процессу рекурсии с отрицательными аргументами в «факт», которая завершается при исчерпании глубины зарезервированных интерпретатором Пролога стеков. Ускорить выход из рекурсии можно, добавив к предикату «факт(1,1)» отсечение!:
факт(1,1):-!.
Однако, использование отсечения требует более подробного рассмотрения. В общем случае последовательность предложений в базе знаний не имеетзначения. Однако это не так для рекурсивно-определенных отношений. Например:
родитель(Х):- родитель(Y),отец(Y,Z).
родитель(коля).
отец(коля,петя).
родитель(петя).
В этом случае в первом предложении голова имеет ту же функцию, что и одна из целей - «родитель». В процессе поиска ответа в этой базе знаний будет применено правило: предложение, стоящее первым, будет применено первым - известное как принцип поиска в глубину.
Это приведет к тому, что система будет обращаться только к первому предложению базы знаний и ответ на вопрос не будет найден никогда (образуется бесконечная петля вывода). Однако небольшое изменение базы знаний - перестановка двух предложений местами - приведет к удачному поиску решения.
Программа 116
родитель(коля).
родитель(X):- родитель(Y), отец(Y,Х).
отец(коля,петя).
? - родитель(петя).
Неограннчено-повторное обращение к предложению можетбыть и более замаскированным так, как это получается в программе 117.
Программа 117
выше(А,В): - ниже(В,А).
ниже(В,А): - выше(А, В).
выше(коля,петя).
?- ниже(петя,коля).
Однако если третье предложение стоит на первом месте, то повторного обращения не произойдет и ответ будет найден.
В общем виде рекурсия на Прологе выглядит так:
Р(1,...).
P(n,...) -Q1,..., Qn, P(n-l,...), R1,... Rm.
Правило Р обращается само к себе, при этом происходит углубление рекурсии. Предикаты Q1,.... Qn выполняются на прямом ходе рекурсии, а R1,..., Rm - на обратном; n - это некоторый условный параметр, входящий в условие продолжения рекурсии, а Р(1,...)- факт, завершающий процесс рекурсии.
Особенно простым случаем рекурсии является простое циклическое повторение. Один из способов организации повторения связан с наличием в базе знаний процедуры вида repeat, repeat: - repeat.
Использование repeat в качестве подцели некоторого правила приводит к многократному повторению остальных подцелей этого правила.






