Существует два способа реализации построения изображений на экране дисплея - векторный (функциональный) и растровый. В первом случае электронный луч поочередно рисует на экране различные знаки - элементы изображения. На современных персональных компьютерах чаще используется растровый способ изображения графической информации, в котором изображение представлено прямоугольной матрицей точек (пикселов), имеющих свой цвет из заданного набора цветов (палитры). Графический режим осуществляет видеоадаптер, управляющий работой электронной трубки и видеопамятью, в которой запоминается текущее изображение. Адаптер обеспечивает регулярное отображение видеопамяти на экране монитора.
Растровое изображение - это совокупность разноцветных точек. Координаты точек определяются декартовой (прямоугольной) системой с началом координат, как правило, в левом верхнем углу экрана. Абсцисса х точки увеличивается слева направо, ордината у - сверху вниз. Таким образом, любая графическая операция сводится к работе с отдельными точками экрана монитора - пикселами. Существуют специальные графические библиотеки программ, которые предназначены для изображения более сложных объектов, являющихся объединением группы пикселов: наиболее употребимые линии, геометрические фигуры, шрифты и т.п.
Большинство языков программирования имеют свои стандартные графические библиотеки. Так, у Бейсика графические команды являются встроенными; системы программирования Турбо-Паскаль содержат графическую библиотеку (модуль Graph, tpu), имеющую в своем составе процедуры и функции обработки простейших графических образов. Тем не менее, многие программисты и разработчики программ предпочитают создавать свои библиотеки графических подпрограмм в соответствии со спецификой своей работы.
В последние годы возрос интерес со стороны пользователей к специальным инструментальным программам машинной графики: графическим редакторам, издательским системам и т.п. В них предоставляется удобный интерфейс для пользователей, автоматизируется большое количество разнообразных действий с графической информацией - от построения простейших рисунков до создания мультипликационных (анимационных) роликов.
Вывод изображения на экран дисплея и разнообразные действия с ним требуют геометрической грамотности, интуиции. Моделирование образной информации на экране дисплея развивает наблюдательность, пространственное воображение, геометрическую интуицию, конструкторские и изобретательские навыки.
ИЗОБРАЗИТЕЛЬНАЯ ГРАФИКА
При работе с художественной графикой, включая компьютерную графику, необходимо знать следующие понятия.
Композиция - строение, соотношение и взаимное расположение частей, сосредоточие идейно-творческого начала, позволяющего автору произведения искусства целенаправленно организовывать главное и второстепенное и добиваться максимальной выразительности содержания и формы в их образном единстве.
Законы композиции:
1) закон цельности: во-первых, наличие конструктивной идеи, объединяющей в единое целое все компоненты произведения; во-вторых, связь и взаимная согласованность всех элементов композиции; в-третьих, неповторимость элементов композиции;
2) закон контрастов: контраст света и тени определяет форму предметов; контрасты величин, построения сюжета определяют композицию. Правила композиции:
1) передача ритма: ритм в удачной композиции одновременно расчленяет компоненты произведения и объединяет их;
2) композиционный центр: выделяется объемом, освещенностью и другими средствами, действующими в соответствии с основными законами композиции.
Мера - характеризует общие принципы строения, целостность предмета,лежит воснове ритма, гармонии, ансамбля в архитектуре.
Симметрия - одинаковость в расположении частей чего-нибудь по противоположным сторонам от точки, прямой или плоскости. Симметрия в композиции создается уравновешенностью ее частей по массам, тону, цвету и форме. Симметрия (геометрическая) - свойство геометрических фигур при котором каждая пара соответственных точек лежит на одном перпендикуляре к данной плоскости по разные стороны и на одинаковом расстоянии от нее.
Пропорция - определенное соотношение частей между собой, соразмерность.
Ритм - равномерное чередование каких-нибудь элементов.
Гармония - соразмерность частей, слияние различных компонентов объекта в единое органичное целое. В истории эстетики гармония - существенная характеристика прекрасного.
Перспектива - искусство изображать на плоскости трехмерное пространство в соответствии с тем кажущимся изменением величины, очертаний, четкости предметов, которое обусловлено степенью отдаленности их от точки наблюдения.
При моделировании графических объектов на экране дисплея используют разные методы и способы представления изображений. Можно выделить два принципа моделирования - случайный и детерминированный. На их основе строятся технологии в изобразительной графике, в которой условно можно выделить три направления: художественное, иллюстративное и демонстрационное.
Объектами художественной графики выступают различные узоры, шрифты и другие изображения. При работе с изображениями широко используют простые мотивы и разнообразный геометрический материал. В частности, простые геометрические фигуры в различных сочетаниях и способах размещения (вложения, вращения, симметрии) используются в «живых картинках» для получения муарового эффекта. Удачное сочетание случайного и упорядоченного в любой пропорции с технологиями расположения графических объектов позволяет создавать художественный дизайн.
Самые простые узоры - бордюры - представляют бесконечный ряд равных плоских фигур, расположенных друг за другом таким образом, что элементарная конечная фигура переносится вдоль одного измерения бесконечно. Помимо элементарного мотива для получения бордюра необходимо выбрать группу симметрии бордюра и задать конкретные образующие этой группы из следующего набора движений плоскости:
• параллельный перенос;
• центральная симметрия;
• осевая симметрия;
• скользящая симметрия.
Для бордюр существует четыре абстрактные группы симметрии, которые определяют семь типов симметрии бордюр:
1) один параллельный перенос;
2) одна скользящая симметрия;
3) две осевые симметрии;
4) две центральные симметрии;
5) одна осевая и одна центральная симметрия;
6) один параллельный перенос и одна осевая симметрия;
7) три осевые симметрии.
Существует несколько способов построения бордюр по заданному элементарному мотиву и системе образующих ее группы симметрии. Рассмотрим наиболее простые из них. Первый способ основан на простом переборе элементов группы - на элементарный мотив действуют поочередно всеми элементами группы симметрии бордюра. Множество полученных образов и будет представлять собой требуемый бордюр. Этот способ неудобен тем, что на каждом этапе необходимо представить очередной элемент группы в виде композиции подходящих степеней образующих.
Второй способ более предпочтителен. На элементарный мотив действуют одним из образующих. Затем на новую фигуру, составленную из исходного мотива и его образа, действуют любым образующим, который не отображает эту фигуру на себя. Получается фрагмент бордюра, состоящий из предыдущей фигуры и ее образа.
Продолжая этот процесс можно построить любую конечную часть бордюра. Преимущество этого способа заключается в том, что на каждом этапе мы будем иметь дело с конкретной симметрией, с нахождением образа конкретной фигуры.
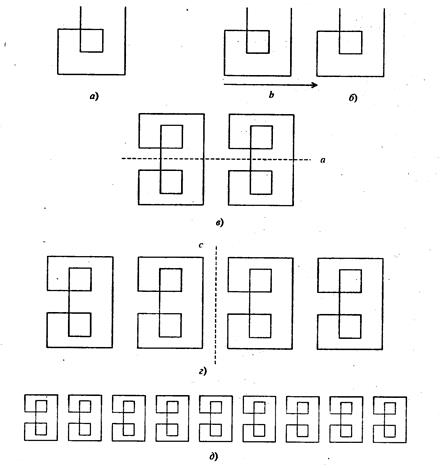
Рис. 2.16. Схема построения бордюра
Рассмотрим, например, процесс построения бордюр с помощью образующих шестого типа симметрии. Создадим элементарный мотив узора (рис. 2.16, а) и определим образующие: параллельный перенос зададим вектором b, (рис. 2.16, б) осевую симметрию прямой а (рис. 2.16, в)
Процесс получения бордюра с помощью заданных образующих вторым из описанных выше способом проиллюстрирован поэтапно. На элементарный мотив действуем параллельным переносом на вектор b, см. схему б. Получим фигуру, состоящуюиз элементарного мотива и его образа. На новую фигуру действуем осевой симметрией с осью а. Получим фигуру, изображенную на схеме в, на которую действуем параллельным переносом 2b. В результате получим новую фигуру, см. схему г. Продолжая этот процесс, получаем фрагмент бордюра нужной длины.
Бордюры используются для окантовки обоев, ковров; для настенной росписи, украшающей здания, подземные переходы; в виде металлических решеток для ограждения парков, мостов и садов и пр.
Более зрелищны, привлекательны и интересны по построению орнаменты. Любой орнамент получается переносом узора с помощью двух параллельных переносов, заданных неколлинеарными векторами. Для любого орнамента можно найти сетку, узлы которой составляют вполне определенную систему равных точек орнамента. Различают пять типов плоских решеток: квадратная, прямоугольная, гексагональная, ромбическая и косая. Тип плоской решетки определяет характер переносной симметрии данного орнамента.
В простейшем случае орнамент характеризуется только переносной симметрией. Для построения такого орнамента надо выбрать соответствующую плоскую решетку, заполнить элементарную ячейку решетки определенным рисунком и затем многократно повторить этот рисунок за счет переносов ячейки без изменения ее ориентации. Для построения более сложных по композиции орнаментов рисунок элементарной ячейки заполняется из основного (элементарного) мотива с помощью образующих этого типа симметрии плоских орнаментов. Существует 17 типов симметрии плоских орнаментов, которые определяются следующим образом:
1) два параллельных переноса:
2) три центральных симметрии;
3) две осевые симметрии и параллельный перенос;
4) две скользящие симметрии с параллельными осями;
5) осевая и скользящая симметрии с параллельными осями;
6) симметрия относительно четырех сторон прямоугольника;
7) одна осевая и две центральные симметрии;
8) две скользящие симметрии с перпендикулярными осями;
9) две осевые симметрии с перпендикулярными осями и одна центральная симметрия;
10). центральная симметрия и вращение на 90°;
11) симметрия относительно трех сторон прямоугольного равнобедренного треугольника;
12) осевая симметрия и вращение на 90°;
13) два вращения на 120°;
14) осевая симметрия и вращение на 120°;
15) симметрия относительно равностороннего треугольника;
16) центральная симметрия и вращение на 120°;
17) симметрия относительно трех сторон прямоугольного треугольника с углом 30°.
Несколько слов о частных случаях орнаментов. Бесконечная плоская фигура Ф называется плоским орнаментом, если выполняются следующие условия: 1) среди перемещений, отображающих Ф на себя, существуют неколлинеарные параллельные переносы; 2) среди всех векторов (параллельных переносов), отображающих Ф на себя, существует вектор наименьшей длины. Фигуру называют линейным орнаментом, если плоская фигура отображается сама на себя при параллельных переносах только одного направления (и противоположного ему), причем среди этих переносов существует перенос наименьшей длины.
Большой интерес представляют паркеты. Паркетом называется разбиение плоскости на многоугольники, при котором каждые два многоугольника либо не пересекаются, либо имеют ровно одну общую вершину, либо имеют общую сторону, причем объединение сторон всех многоугольников является плоским орнаментом. Паркет называется правильным, если все многоугольники разбиения правильные (возможно с различным числом сторон) и любую величину паркета можно перевести в любую другую величину некоторым перемещением, отображающим весь паркет на себя.
Интересны орнаменты, заполненные одинаковыми фигурками без промежутков. Фигурку такого орнамента можно создать с помощью геометрических преобразовании на основе гексагональной сетки.
Процесс моделирования орнаментов на экране компьютера аналогичен моделированию бордюр: после получения повторяющейся фигурки из элементарного мотива с помощью образующих данного орнамента вывод на экран происходит циклическим изменением координат в двух направлениях. При моделировании орнаментов на основе различных плоских решеток без «заполнения» их элементарной ячейки получаются паркеты. Для осуществления компьютерного моделирования графического объекта выбирают подходящее программное инструментальное средство - графический редактор (систему), например, PaintBrash, CorelDraw и т.п., в котором допустимы все возможности, необходимые для описанной работы. Иногда бывает полезным осуществить построение графического образа программированием (на одном из языков программирования) с использованием графических библиотек.
Узор на плоскости получается из элементарного мотива с помощью образующих элементов его группы симметрии. Для бордюр существует 7 различных наборов образующих его групп симметрии, для орнаментов - 17. Чтобы построить узор на компьютере, необходимо
1) создать элементарный мотив узора (в графическом редакторе,на языке программирования, сканированием с листа бумаги);
2) выбрать и задать образующие;
3) построить образы каждой точки элементарного мотива по его образующим, т.е. получить из элементарного мотива изображение конечной повторяющейся фигуры;
4) средствами имеющегося компьютера и программного обеспечения размножить получившийся «шаблон» (фигурку), циклически меняя координаты в одном или в двух направлениях.
В художественной графике часто обращаются к узорам, получаемым в результате «интерференции» при наложении каких-либо семейств кривых. При пересечении, например, двух семейств прямых под заданным углом получаются «муаровые» эффекты, рис. 2.17.
Моделирование муаровых узоров представляет простой, но занимательный процесс, в котором основная роль принадлежит зрительному восприятию исследователя, который, меняя параметры семейств кривых и их способы пересечения, добивается наилучшей в смысле гармонии красоты узоров.
Используя принцип муаровых узоров, можно моделировать на экране дисплея фейерверки. Простейший одиночный фейерверк можно изобразить по следующему принципу. Из фиксированной точки (x, у) строят отрезки прямых в точку, задаваемую случайным образом и случайным цветом. Возникающие одиночные фейерверки, пересекаясь друг с другом, создают красивые картинки.
Узоры можно моделировать с помощью простых мотивов, в частности, штрихованного угла. Штрихованный угол задается координатами трех точек и изображается семейством отрезков, соединяющих точки разбиения сторон угла с одинаковыми номерами. Подобные мотивы удобно оформлять в виде подпрограммы, а затем использовать при моделировании различных изображений.

. Рис. 2.17. Муаровый pop
Сочетание случайного и упорядоченного в любой пропорции при изображении графических объектов дает эффект. Например, на основе простого мотива - угла, вершина которого находится на горизонтальной прямой, - можно изобразить «лес». При упорядоченном размещении «деревьев» имеем «посадку».
Подобные технологии широко используют в иллюстративной графике. В настоящее время иллюстративная графика, в первую очередь, связана с изображением графического материала в издательских системах.
Иллюстративный материал - схемы, эскизы, географические карты, чертежи и др. -можно создавать различными графическими редакторами, системами. Здесь важна легкость и быстрота формирования и преобразования графических изображений для тех или иных приложений. В последнее время большой интерес вызывает иллюстративный материал, представленный в демонстрационной, динамической форме.
Демонстрационная графика связана с динамическими объектами. Втехнологииизображения динамических объектов используют три основных способа: рисование -стирание, смену кадров (страниц), динамические образы.
Достаточно просто организовать перемещение фрагмента рисунка на экране. Для этого надо
• создать этот фрагмент в нужном месте экрана;
• стереть фрагмент, рисуя его цветом фона или используя процедуру очистки экрана;
• снова нарисовать фрагмент в другом месте экрана, и так далее.
Еще один способ организации движения объектов на экране, широко применяющийся в компьютерных играх, связан с использованием нескольких экранных страниц. В любой момент времени одну из страниц можно сделать видимой и посмотреть ее содержимое на экране. Визуальная страница обычно пассивна, т.е. на ней нельзя выполнять графические процедуры. Другую страницу можно объявить активной. Активная страница невидима для пользователя, но на ней можно подготовить другой рисунок. Меняя страницы ролями, можно создать мультипликационный сюжет
В обучающих программах и в компьютерных играх часто используют динамические образы (в том числе спрайты). При этом используют динамическую память для хранения прямоугольных фрагментов рисунков и последующего вывода их в нужное место экрана.
ГРАФИЧЕСКИЕ РЕДАКТОРЫ
Создать объекты иллюстративной графики, включая динамические ролики, можно средствами программирования, а также графическими редакторами и системами. Рассмотрим два из них.
Редактор Paint
Графический редактор Paint, входящий в комплект стандартных программ MS Windows 95, позволяет, используя манипулятор «мышь», выполнять черно-белые и цветные рисунки, обрамлять их текстом, выводить на печать. В Paint можно работать с фрагментами графических изображений: копировать, перемещать, поворачивать, изменять размеры, записывать на диск и считывать с диска. С помощью Paint можно обрабатывать графические изображения, а также считывать и записывать в файл полностью или частично изображение с дисплея, если монитор работает в графическомрежиме.

Рис. 2.18. Рабочее окно программы Paint
После загрузки пакета появляется рабочий экран редактора (рис. 2.18). Большую часть экрана занимает рабочее поле, окрашенное в фоновый цвет. Над рабочим полем - меню, позволяющее выполнять команды редактирования. Слева от рабочего поля расположена панель инструментов, на которой высвечен инструмент, в данный момент являющийся рабочим. Под рабочим полем находится палитра. С левого края палитры показаны два вложенных квадрата, внутренний из которых окрашен в рабочий цвет, а внешний - в фоновый. В левом нижнем углу экрана выводится калибровочная шкала, которая позволяет устанавливать ширину рабочего инструмента (кисти, резинки и т.д.). Установленная в данный момент ширина инструмента отмечена стрелкой. Вдоль нижнего правого и правого края рабочего поля находятся линейки прокрутки для перемещения рабочего поля по картинке, если размеры картинки больше размеров рабочего поля.
Общие правила работы с редактором таковы. Для выбора (установки) параметров работы и выполнения команд в Paintbrush необходимо поместить указатель мыши на пункт меню и щелкнуть левой кнопкой. Выход из программы: File/Quit.
Программа Freeze предназначена для сохранения выводимого на экран изображения в графическом PCX-файле с одновременным сохранением оформления экрана, возможностью последующего редактирования данного изображения и вставки его в качестве иллюстрации в текстовые редакторы и настольные издательские системы. Установка программы происходит автоматически при запуске Paintbrush.
Редактор CorelDraw
Начиная работать с графическим редактором CorelDraw, мы прежде всего видим его рабочее окно, рис. 2.19.

Рис. 2.19. Рабочее окно программы CorelDraw
Чтобы активизировать меню выбора (установки) параметров работы или выполнения команд, установите указатель мыши на пункт меню и щелкните левой кнопкой или нажмите клавишу Alt и клавишу, соответствующую выделенной букве. В некоторых случаях для облегчения выполнения наиболее часто употребляемых команд ввод их с клавиатуры осуществляется нажатием комбинации клавиш или определенной клавиши. Выполнение команд происходит после подтверждения правильности установки всех параметров или выбора значений активизацией экранной кнопки ОК в диалоговой панели или нажатием клавиши Enter.
Выход из меню - переместить указатель мыши за пределы меню и щелкнуть кнопкой или нажать клавишу Esc.
Выход из программы: File/Quit или Alt + F4.
Для вызова диалоговой панели выбора (установки) параметров работы или выполнения команд необходимо установить указатель мыши на пункт меню или команду и щелкнуть кнопкой или нажать клавишу Alt и клавишу, соответствующую выделенной букве. Выполнение команд происходит после подтверждения правильности установки всех параметров (выбора значений) активизацией экранной кнопки ОК или нажатием клавиши Enter.
Для редактирования рисунка следует активизировать пиктограмму с помощью мыши или нажатием клавиши Пробел, переместить указатель на любую точку контура рисунка и щелкнуть кнопкой. Выбранный рисунок будет окружен восемью квадратами черного цвета. Можно выделить одновременно несколько объектов, последовательно выбирая их с помощью мыши при нажатой клавише Shift или отмечая на экране прямоугольную область, в которой они расположены. Для одновременного выбора всех рисунков на экране необходимо активизировать пиктограмму, переместить указатель мыши в один из углов выбираемого прямоугольного контура, нажать кнопку и, не отпуская ее, переместить указатель в противоположный угол и отпустить кнопку. Контур будет изображен штриховой линией. Для отмены выбора - переместить указатель мыши за контур и щелкнуть кнопкой.
Для изменения масштаба выводимого на экран рисунка необходимо активизировать соответствующую пиктограмму.
Работа с текстом начинается с активизации пиктограммы текста. Для перемещения по тексту в диалоговой панели Техt необходимо переместить указатель мыши и щелкнуть левой кнопкой. Однако в программе для перемещения предусмотрены также специальные клавиши.
Для выделения фрагмента текста необходимо активизировать пиктограмму с помощью мыши или клавиши Пробел. Переместите указатель мыши в один из углов выбираемого прямоугольного контура, нажмите кнопку К, не отпуская ее, переместите указатель в противоположный угол, отпустите кнопку. Весь контур будет окружен штриховой линией. Для выделения отдельного символа 'необходимо активизировать пиктограмму, переместить указатель мыши в один из углов выбираемого прямоугольного контура, нажать кнопку и, не отпуская ее, переместить указатель в противоположный угол. Выбранный объект не будет окружен рамкой из квадратов, однако на нем будут выделены все узловые точки. Выбор нескольких символов осуществляется аналогично при нажатой клавише Shift.
Прежде чем начать оформление ранее введенного текста, его необходимо выделить одним из выше описанных способов.
ДЕЛОВАЯ ГРАФИКА
Одним из первых приложений компьютерной графики стало отображение данных экономических расчетов.
Графические представления расчетных и статистических данных удобно представлять в виде схем, диаграмм, гистограмм и графиков. Различают следующие их виды:
гистограмма - группастолбцов, пропорциональных по высоте определенным числовым значениям;
круговая диаграмма - секторы круга, углы которых пропорциональны элементам данных;
линейный график - отображение исходных величин в виде точек, соединенных отрезками прямых линий;
временная диаграмма - последовательность операцийили процессов определенной длительности (измерение динамических процессов);
структурная схема - представление сложных объектов в виде дерева или графа;
круговая гистограмма - представление относительных величин объектов, которым на изображении сопоставляются размеры и расположение кругов в прямоугольной системе координат.
Из числа средств прикладного программного обеспечения общего назначения графическое представление данных лучше всего развито в электронных таблицах и в СУБД.
Одним из первых практических применений машинной графики было автоматическое построение графиков функции в различных системах координат. Обычно графики функций строят в декартовых координатах (в прямоугольной системе, рис. 2.20).

Рис. 2.20. Построение на экране графиков функций (в декартовой системе координат)
В общем виде алгоритм построения графика заданной функции у = f(х) на отрезке [а, b] заключается в следующем.
1. Определяем область значений функции, для чего найдем максимальное по модулю значение функции на заданном отрезке [а, b], т = max(abs (f (x)) для всех x из [а, b].
Примем для удобства, что минимальное значение функции на отрезке совпадает с максимальным, но с обратным знаком. Таким образом, область значений функции лежит в интервале [-т, т].
Поиск максимума можно осуществить разными способами, например, табулируя функцию f(x) на отрезке с разбиением на n частей и определяя максимальное значение в массиве чисел Yi =f(xi), где xi = а + i- (b - а) / п, для i = 0,... п.
2. Задаем координаты окна x0, y0, x1, у1 на графическом дисплее, в котором будем строить график функции.
3. Формулы преобразования координат х, у точек прямоугольника [а, b]∙[-т, т] обычной декартовой системы в соответствующие координаты и, v окна [x0, x1] ∙ [у0,y1] графического экрана можно задать в следующем виде:
и = x0 + (x - а)(х 1 - x0)/(b - а),
v = (y0 + y1) / 2 – f(x) (y1 – y0) / (2m).
Тогда автоматическое построение графика функции на экране дисплея осуществляется путем установки точек (иi, vi), соответствующих точкам (xi f(xi)), выбранным в декартовой системе. Часто бывает полезно соединять полученные точки отрезками или специальными линиями, что программы могут делать (или не делать) по пожеланию пользователя.
4. Далее можно оформить график, нарисовав оси координат, нанести масштабные сетки, вывести соответствующие обозначения и комментарии. Оси координат на графическом экране в заданном окне легко построить, вычислив экранные координаты начала выбранной декартовой системы {xv,yv):
xv = х0 - а(х1 - x0)/(b - а),
yv=(y0+y1) / 2.
ИНЖЕНЕРНАЯ ГРАФИКА
Компьютеризацию чертежных и конструкторских работ проводят давно и в настоящее время используют различные системы автоматизации проектных работ (САПР). Аббревиатуру САПР впервые использовал основоположник этого научного направления Айвен Сазерленд в своих лекциях, прочитанных в Массачусетском технологическом институте в начале 60-х годов. Фактически инженеры применяли компьютеры для решения сложных задач проектирования еще в эпоху ранних послевоенных моделей универсальных компьютеров, а первые образцы специализированного оборудования САПР были созданы уже в середине 50-х годов. Однако широкое распространение САПР обусловлено появлением микропроцессорной техники, предоставившей возможности создавать, модифицировать и обрабатывать сложные графические изображения на экране монитора.
В настоящее время САПР обозначает аппаратно-программный комплекс, поддерживающий процесс проектирования с использованием специальных средств машинной графики, поддерживаемых пакетами программного обеспечения, для решения задач, связанных с проектной деятельностью. В совокупности развитая САПР представляет собой специализированную информационную систему. Сфера применения САПР охватывает такие разные области приложения, как архитектура, гражданское строительство, картография, медицина, геофизика, разработка моделей одежды, издательское дело, реклама.
Полная система САПР состоит из компонентов аппаратного и программного обеспечения. Общими компонентами аппаратного обеспечения системы САПР являются ЦП (центральный процессор), несколько рабочих станций, разделяемая между рабочими станциями периферия.
Состав типичной системы САПР:
дисплей (графический и алфавитно-цифровой);
процессор;
клавиатура;
устройство управления курсором (мышь, дигитайзер);
электронный командный планшет;
принтер.
Одним из наиболее давних и популярных средств автоматизированного проектирования является система АВТОКАД (AutoCad). АВТОКАД не является проблемно-ориентированной системой, т.е. не содержит специализированныхбаз данных, экспертных систем и многого из того, что входит в состав специализированной интеллектуальной САПР. АВТОКАД - достаточно простая универсальная система. Ее возможности таковы:
· развитая система экранныхменю;
· высокая точность графической информации;
· разбивка информации (расслоение);
· прочерчиванне на дисплее координатной сетки;
· средство захвата графических объектов;
· мощное редактирование;
· отображение параметров графических характеристик;
· полуавтоматическая и автоматическая простановка размеров;
· штриховка;
· работа с блоками.
После запуска АВТОКАДа на текстовом экране появляется главное меню:
О - выход;
1 - создание нового чертежа;
2-редактирование существующего чертежа;
3 - вывод на плоттер (графопостроитель);
4 - вывод на принтер;
5-конфигурация;
б - файловые утилиты;
7-шрифты;
8 -стыковка со старыми версиями.
Режимы экранного меню:
AUTOCAD - выход в головное меню;
* * * * - режим объектного захвата;
BLOCKS -работа с блоками;
DISPLAY - работа с изображением без его изменения;
SETTINGS -настройка;
DIM - обезразмеривание;
EDIT -редактирование;
DRAW -рисование;
LAYER -работа со слоями;
INQUIRY -справки о примитивах;
UTILTTS - выход в ДОС, запись чертежей в разных форматах;
PLOT -получение твердой копии и т.д.
В режиме DRAW (рисуй) имеется возможность строить графические примитивы
и проводить с их помощью синтез изображений. Например, здесь существует восемь
способов рисования дуг:
· по трем точкам на дуге /З points/;
· по начальной точке, центру и длине хорды /S, С, L/;
· по начальной точке, центру и заключенному углу /S, С, А/;
· по начальной точке, конечной точке и радиусу /S, Е, R/;
· по начальной точке, конечной точке и заключенному углу /S, Е, А/;
· по начальной точке, конечной точке и исходному направлению /S, Е, D/;
· по продолжению предыдущей линии или дуги /CONTIN:/.
Можно выделить следующие правила изображения дуги:
1) обычно дуга строится против часовой стрелки от точки к точке;
2) если есть в выбранной опции возможность задать угол, то отрицательный угол позволяет рисовать дугу по часовой стрелке;
3) по умолчанию дуга рисуется по начальной, промежуточной и конечной точкам.
При выборе в основном меню АВТОКАД режима Edit имеется возможность стирать созданные объекты, возвращать случайно стертые, перемещать и копировать, вычерчивать сопряжения между двумя существующими объектами, снимать фаски, разбивать объект на части, зеркально отображать, поворачивать, увеличивать и уменьшать, отсекать и т.п.
Практически все команды редактирования запрашивают выбор одного или нескольких объектов для обработки. Совокупность таких объектов называется набором выбора. Когда АВТОКАДу требуется не один объект, а набор выбора, появляется подсказка Select objects: (выбрать объекты) и на экране вы видите маленький прямоугольник - мишень для выбора объектов. Способы выбора объектов указываются в опциях соответствующей команды.
НАУЧНАЯ ГРАФИКА
Компьютерная графика представляет значительный интерес для научных исследований. В частности, она выступает как средство формирования научной документации с использованием специальной нотации - математических знаков, индексов, шрифтов и т.п. В последнее время ученые чаще стали обращаться к имитационному моделированию на компьютере.
В компьютерной графике большое значение имеют методы и способы геометрического моделирования. Модели, геометрические преобразования составляют в настоящее время основу теории компьютерной графики и геометрического моделирования. Аналитические модели - это набор чисел, логических параметров, играющих роль коэффициентов в уравнениях, которые задают графический объект заданной формы. Например, аналитической моделью окружности на плоскости в параметрической форме являются уравнения
x=x0+R-cosA,
y=y0+R-sinA,
где х0, у0 - координаты центра, R - радиус, А - угол. Параметрическое задание образов широко применяется в машинной графике и геометрии. Изображение окружности можно осуществить установкой последовательных точек (близко расположенных), изменяя генерирующий параметр А от 0 до 360°.
Координатные модели - это массивы координат точек, принадлежащих объектам. Например, поверхность задается массивом точек Z = f (x, у) на координатной сетке [хi, yj}. Если точки в модели расположены в том же порядке, что и на линии образа, то модели называют упорядоченными. Помимо координат, в модели могут быть указаны дополнительные характеристики проекции касательных или нормальных векторов.
Приближенные модели содержат аппроксимации кривых методами вычислительной геометрии. Например, изображение гладких кривых можно осуществить ломаными линиями: линейными, параболическими или сплайнами. Используя вышеперечисленные геометрические модели, можно создавать различные демонстрационные картины. Например, модель Солнечной системы для наглядности удобно представить в динамической форме. Организуем движение точки (Земли) по окружности, в центре которой размещается круг (имитация Солнца). Установку точки на орбите осуществим по параметрическим формулам окружности:
X0 = 320 + r1∙sin(A1);
Y0 = 240 + rl ∙cos(Al),
где r1 - радиус орбиты Земли, А1 - параметрический угол, меняющийся от 0 до 360°. Чтобы организовать движение, достаточно в цикле устанавливать точку с координатами (x0, у0) для всех углов А1, принимающих значения от 0 до 360° с шагом h. Аналогичная процедура справедлива и для второй точки (Луны), которая изображается по подобным формулам, в которых центр орбиты (Земля) является подвижным:
х = х0 + r ∙ sin(A);
у = у0 + r ∙ cos(A),
где r - радиус орбиты Луны, А - угол вращения.
Контрольные вопросы и упражнения
1. Составьте каким-либо средством машинной графики бордюры каждого типа симметрии из следующих элементарных мотивов, рис. 2.21.
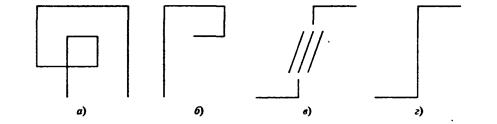
Рис. 2.21.
2. Постройте орнаменты различного типа симметриииз выбранного произвольного элементарного мотива каким-либо средством машинной графики.
3. Задана высота (м) над уровнем моря вершин: Мак-Кинли - 6200, Логан - 6100, Элберт - 440, Робсон - 4000, Митгелл - 2000. Составьте по этим данным столбчатую диаграмму.
4. По данным упражнения 3 составьте круговую диаграмму.
5. Постройте график функции у = x sin (1/x).
6. Создайте мультипликацию: вращение электрона в модели атома.
7. Изобразите шестиугольную призму.
8. Подготовьте иллюстрацию ко Дню учителя.
9. Организуйте в школе (вузе) компьютерный вернисаж.






