С точки зрения изучения принципов представления и обработки информации в компьютере, обсуждаемые в этом пункте системы представляют большой интерес.
Хотя компьютер «знает» только двоичную систему счисления, часто с целью уменьшения количества записываемых на бумаге или вводимых с клавиатуры компьютера знаков бывает удобнее пользоваться восьмеричными или шестнадцатиричными числами, тем более что, как будет показано далее, процедура взаимного перевода чисел из каждой из этих систем в двоичную очень проста - гораздо проще переводов между любой из этих трех систем и десятичной.
Перевод чисел из десятичной системы счисления в восьмеричную производится (по аналогии с двоичной системой счисления) с помощью делений и умножений на 8. Например, переведем число 58,32(10):
58: 8 = 7 (2 в остатке),
7: 8 = 0 (7 в остатке).
0,32 • 8 = 2,56,
0,56 • 8 = 4,48,
0,48-8=3,84,...
Таким образом,
58,32(10) =72,243... (8)
(из конечной дроби в одной системе может получиться бесконечная дробь в другой).
Перевод чисел из десятичной системы счисления в шестнадцатеричную производится аналогично.
С практической точки зрения представляет интерес процедура взаимного преобразования двоичных, восьмеричных и шестнадцатиричных чисел. Для этого воспользуемся табл. 1.6 чисел от 0 до 15 (в десятичной системе счисления), представленных в других системах счисления.
Для перевода целого двоичного числа в восьмеричное необходимо разбить его справа налево на группы по 3 цифры (самая левая группа может содержать менее трех двоичных цифр), а затем каждой группе поставить в соответствие ее восьмеричный эквивалент. Например:
11011001= 11011001, т.е. 11011001(2) =331(8).
Заметим, что группу из трех двоичных цифр часто называют «двоичной триадой».
Перевод целого двоичного числа в шестнадцатиричное производится путем разбиения данного числа на группы по 4 цифры - «двоичные тетрады»:
1100011011001 = 1 1000 1101 1001, т.е. 1100011011001(2)= 18D9(16).
Для перевода дробных частей двоичных чисел в восьмеричную или шестнадцатиричную системы аналогичное разбиение на триады или тетрады производится от точки вправо (с дополнением недостающих последних цифр нулями):
0,1100011101(2) =0,110 001 110 100 = 0,6164(8),
0,1100011101(2) = 0,1100 0111 0100 = 0,C74(16).
Перевод восьмеричных (шестнадцатиричных) чисел в двоичные производится обратным путем - сопоставлением каждому знаку числа соответствующей тройки (четверки) двоичных цифр.
Таблица 1.6 Соответствие чисел в различных системах счисления
| Десятичная | Шестнадцатиричная | Восьмеричная | Двоичная |
| А | |||
| В | L011 | ||
| С | |||
| D | |||
| E | |||
| F |
Преобразования чисел из двоичной в восьмеричную и шестнадцатиричную системы и наоборот столь просты (по сравнению с операциями между этими тремя системами и привычной нам десятичной) потому, что числа 8 и 16 являются целыми степенями числа 2. Этой простотой и объясняется популярность восьмеричной и шестнадцатиричной систем в вычислительной технике и программировании.
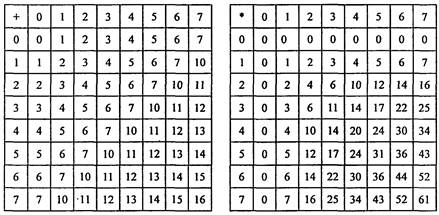
Арифметические действия с числами в восьмеричной и шестнадцатиричной системах счисления выполняются по аналогии с двоичной и десятичной системами. Для этого необходимо воспользоваться соответствующими таблицами. Для примера табл. 1.7 иллюстрирует сложение и умножение восьмеричных чисел.
Рассмотрим еще один возможный способ перевода чисел из одной позиционной системы счисления в другую - метод вычитания степеней. В этом случае из числа последовательно вычитается максимально допустимая степень требуемого основания, умноженная на максимально возможный коэффициент, меньший основания; этот коэффициент и является значащей цифрой числа в новой системе. Например, число 114(10):
114 - 26 = 114 – 64 = 50,
50 - 25 = 50 – 32 = 18,
18 - 24 = 2,
2 - 21 = 0.
Таким образом, 114(10) = 1110010(2).
114 – 1 ∙ 82 = 114 – 64 = 50,
50 – 6 ∙ 81 = 50 – 48 = 2,
2 – 2 ∙ 8° = 2 – 2 = 0.
Итак, 114(10)= 162(8).
Таблица 1.7 Таблицы сложения и умножения в восьмеричной системе
Сложение Умножение
Контрольные вопросы
1. В чем отличие позиционной системы счисления от непозиционной?
2. Каковы способы перевода чисел из одной системы счисления в другую?
3. В чем заключается преимущество использования восьмеричной и шестнадцатиричной систем счисления в вычислительной технике?
4. Как выглядят таблицы сложения и умножения в шестнадцатиричной системе?
КОДИРОВАНИЕ ИНФОРМАЦИИ.
АБСТРАКТНЫЙ АЛФАВИТ
Информация передается в виде сообщений. Дискретная информация записывается с помощью некоторого конечного набора знаков, которые будем называть буквами, не вкладывая в это слово привычного ограниченного значения (типа «русские буквы» или «латинские буквы»). Буква в данном расширенном понимании - любой из знаков, которые некоторым соглашением установлены для общения. Например, при привычной передаче сообщений на русском языке такими знаками будут русские буквы - прописные и строчные, знаки препинания, пробел; если в тексте есть числа - то и цифры. Вообще, буквой будем называть элемент некоторого конечного множества (набора) отличных друг от друга знаков. Множество знаков, в котором определен их порядок, назовем алфавитом (общеизвестен порядок знаков в русском алфавите: А, Б,..., Я).
Рассмотрим некоторые примеры алфавитов.
1, Алфавит прописных русских букв:
А Б В Г Д Е Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Ъ Ы Ь Э Ю Я
2. Алфавит Морзе:

3. Алфавит клавиатурных символов ПЭВМ IBM (русифицированная клавиатура):

4. Алфавит знаков правильной шестигранной игральной кости:

5. Алфавит арабских цифр:
6. Алфавит шестнадцатиричных цифр:
0123456789ABCDEF
Этот пример, в частности, показывает, что знаки одного алфавита могут образовываться из знаков других алфавитов.
7. Алфавит двоичных цифр:
0 1
Алфавит 7 является одним из примеров, так называемых, «двоичных» алфавитов, т.е. алфавитов, состоящих из двух знаков. Другими примерами являются двоичные алфавиты 8 и 9:
8. Двоичный алфавит «точка, «тире»:. _
9. Двоичный алфавит «плюс», «минус»: + -
10. Алфавит прописных латинских букв:
ABCDEFGHIJKLMNOPQRSTUVWXYZ
11. Алфавит римской системы счисления:
I V Х L С D М
12. Алфавит языка блок-схем изображения алгоритмов:

13. Алфавит языка программирования Паскаль (см. в главе 3).






