2.1 Определим количество лагов для двух переменных

Лаг 2 H0: 1
H1: 2
H0 – отвергается, лага минимум 2
Лаг 3 H0: 2
H1: 3
H0 – не отвергается, лага 2
Лаг 4 H0: 3
H1: 4
H0 – не отвергается, лага 3
Выбираем между количеством лагов 2 и 3, информационные критерии говорят в пользу лага 2.
Соответственно лагов 2.
2.2 Построим модель VAR для двух переменных. Переменные обозначим за эндогенные


2.3 Проверим данную модель на стационарность:
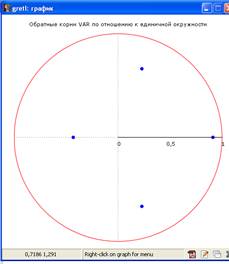
Все корни лежат в единичном круге, значит, модель стационарна.
2.4 Проверим, правильно ли мы выбрали два лага
Уравнение 1 
Уравнение 2 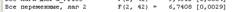
Лаг 2 оказался не значимым.
2.5 Проверим, правильно ли мы включили все переменные в эндогенные переменные:


 Oil Price
Oil Price
Oil является причиной по Грейнжеру для Price, Price является причиной по Грейнжеру для Oil. Получается, что каждый из рядов является причиной для другого ряда. Такого быть не может, причинность по Грейнджреу может возникать только в одну сторону. Следовательно, можно сделать вывод, что ни один из рядов не является причиной для другого по Грейнджеру.
2.6 Являются ли остатки белым шумом:

Включая 2 лаг, автокорреляции нет.
2.7 Проверим остатки модели на нормальность:

Нулевая гипотеза, о том, что выборка тянется из нормального распределения, отвергается.
Построение модели ARIMA для ряда с данными об объеме экспорта.
3.1 Рассмотрим коррелограмму для первой разности ряда Oil:

Из коррелограммы можно сделать вывод, что можно попробовать оценить модель d_Oil c AR(1) AR(2) AR(3) MA(1).

Коррелограмма приемлемая, то есть остатки похожи на белый шум.
Таким образом, можно сделать вывод, что моделью для ряда с данными об объеме экспорта нефти ARIMA(3,0,1).
3.2 Построим прогноз и доверительный интеравал для прогноза.
Ограничим выборку с 2000:1-2012:2 до 2000:1-2009:4. Построим еще раз модель ARIMA(3,0,1) для ограниченной выборки.

Построим прогноз и доверительный интервал.
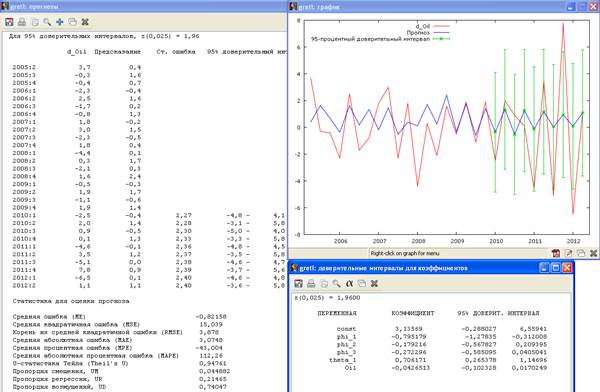
Таким образом, видно что прогноз на 2010 год давольно-таки точен. Самое большое отклонение в первом квартале 2010 в 2,1 единицы. После 2011 года значения прогноза больше отличаются от значения реального ряда. Это можно объяснить тем, что модели ARMA не дают качественного долгосрочного прогноза. С другой стороны, прогноз верно отражает динамику ряда и реальный ряд практически не выходит за границы доверительного интервала прогноза. Таким образом, качество прогноза можно считать приемлемым.
Тест Ингла-Грейнжера на коинтеграцию рассмотренных рядов
Так как ряды Oil и Price имеют разные порядки интегрируемости, соответственно 0 и 1, то коинтеграции между рядами быть не может.






