Исходные данные
Даны два ряда: объем экспорта сырой нефти в млн., тонн и средняя цена нефти $ за баррель России с 2000 по 2012 год. Данные квартальные. Указаны на сайте ЦБ РФ http://www.cbr.ru/statistics/print.aspx?file=credit_statistics/crude_oil.htm&pid=svs&sid=vt1.
Рассмотрим совместный график этих двух рядов:

Из графика можно видеть, что ряды изменяются похожим образом, из чего можно сделать вывод о том, что между ними может быть коинтеграция.
От каких показателей может зависать объемы экспорта сырой нефти? Играет ли в этом роль средняя стоимость нефти за баррель?
Рассмотрим гипотезу о том, что объем экспорта нефти зависит от цены.
Определение порядка интегрируемости
Для определения порядка интегрируемости проведем расширенный тест Дики-Фулера для каждого из рядов.
1.1. Определение порядка интегрируемости для ряда с данными об объеме экспорта нефти.
Для проверки гипотезы H0: Oil – DS (порядок интегрируемости ряда не меньше 1)
против альтернативы H1: Oil – TS (порядок интегрируемости равен 0).
Тест без константы.
Оцененная t-статистика коэффициента при Oil(t-1) равна 0,23, что больше t-крит. при 5% уровне значимости = -1,95. Значит гипотеза не отвергается.
Тест с контстантой.
Оцененная t-статистика коэффициента при Oil(t-1) равна -3,2, что меньше t-крит. при 5% уровне значимости = -2,93 Нулевая гипотеза отвергается.
Тест с константой и трендом.
Оцененная t-статистика коэффициента при Oil(t-1) равна -2,10 что больше t-крит. при 5% уровне значимости = -3,5. Нулевая гипотеза не отвергается.
Также в пользу теста с константой говорят информационные критерии AIC и BIC. (имеют меньшее значение)

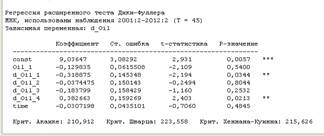
С помощь метода МНК постром модель, проверим автокореляцию в остатках и гетеростатичность.
Р-значение больше уровня значимости, значит автокорреляции нет и модель стационарна.

Следовательно, ряд Oil имеет нулевой порядок интегрируемости.
1.2 Определение порядка интегрируемости для ряда с данными о цене экспортируемой нефти.
Для проверки гипотезы H0: Price – DS (порядок интегрируемости ряда не меньше1)
против альтернативы H1: Price – TS (порядок интегрируемости равен 0).
Тест без константы.
Оцененная t-статистика коэффициента при Price (t-1) равна 0,93, что больше t-крит. при 5% уровне значимости = -1,95. Значит гипотеза не отвергается.
Тест с контстантой.
Оцененная t-статистика коэффициента при Price(t-1) равна -0,47, что больше t-крит. при 5% уровне значимости = -2,93. Значит гипотеза не отвергается.
Тест с константой и трендом.
Оцененная t-статистика коэффициента при Price(t-1) равна -3,47 что больше t-крит. при 5% уровне значимости = -3,5. Нулевая гипотеза не отвергается.


Для продолжения исследования рассмотрим гипотезу H0: d_Price – DS (порядок интегрируемости ряда не меньше 2)
против альтернативы H1: d_Price – TS (порядок интегрируемости равен 1).
Тест без константы.
Оцененная t-статистика коэффициента при d_Price (t-1) равна -6.32, что меньше t-крит. при 5% уровне значимости = -1,95. Значит гипотеза отвергается.
Тест с контстантой.
Оцененная t-статистика коэффициента при d_Price(t-1) равна -6,52, что меньше t-крит. при 5% уровне значимости = -2,93. Значит гипотеза отвергается.
Тест с константой и трендом.
Оцененная t-статистика коэффициента при d_Price(t-1) равна -6,5 что меньше t-крит. при 5% уровне значимости = -3,5. Нулевая гипотеза отвергается.
Тренд и константа оказались не значимы.
Таким образом, ряд Price имеет первый порядок интегрируемости – сам он не стационарен, а его первая разность стационарна.


Убедимся, что ошибки являются белым шумом с помощью МНК.
Автокорреляции в модели не обноружено, но тест на гетероскедастичность не прошел. Уровень значимости меньше принятого.







