Научное познание постоянно и активно использует различные модели реального мира. Что такое модели и метод моделирования – об этом пойдет речь в этой главе.
§ 1. Модели и пределы
Начнем с рассмотрения примеров различных моделей, используемых в науке. В физике могут использоваться различные модели пространства, объектов и процессов. Идеальный газ, абсолютно твердое тело, абсолютно черное тело, линия, плоскость, точка – вот только некоторые примеры физико-математических моделей. Множество моделей мы можем найти в биологии – идеальная популяция со свободным скрещиванием, модель нейрона, модель роста живой системы. В психологии можно найти примеры моделей сознания и личности, различные модели поведения и мотивации. В истории и социологии мы сталкиваемся с моделями общества и его развития, моделями рынка и революций, и т.д.
Подойти к пониманию природы модели нам поможет один исторический пример. Великому итальянскому ученому Галилею принадлежит заслуга открытия первого закона механики – закона инерции. Закон – также один из примеров научной модели. Галилей рассуждал здесь примерно следующим образом.
Предположим, что по плоской поверхности движется некоторое тело Т. Оно движется после некоторого первоначального толчка и в конце концов останавливается из-за силы трения F, пройдя до остановки расстояние R. Такую ситуацию мы часто встречаем в повседневной жизни, например, толкая по льду санки или подталкивая ногой лежащий на полу предмет. Пройдя некоторое расстояние, предмет останавливается. Но Галилей не ограничивается этим общеизвестным фактом, он начинает его видоизменять далее. Галилей задает вопрос, а что будет происходить, если при той же первоначальной скорости движения сила трения F начнет уменьшаться? По-видимому, тело начнет проходить все большие расстояния R. Если через Fi обозначить силу трения, то через Ri можно обозначить проходимое телом расстояние до полной остановки при этой силе трения. Если мы рассматриваем ситуации со все меньшими силами трения F1 > F2 > F3 > …, то им будут соответствовать случаи все больших расстояний, проходимых телом: R1 < R2 < R3 < … И это еще кажется вполне обычным. Но вот далее Галилей делает некоторый совершенно необычный шаг, который и привел его к формулировке закона инерции. Галилей переходит к пределу – он начинает рассматривать казалось бы невозможную ситуацию, когда сила трения полностью отсутствует, т.е. F=0. В этом случае расстояние R также достигнет предельной величины, равной бесконечности, т.е. тело после первоначального толчка должно будет двигаться вечно, никогда не останавливаясь. Согласитесь, такой ситуации уже никто из нас никогда не встречал, хотя она и получена из последовательности обычных ситуаций. Вот это и есть один из основных методов построения моделей, который теперь можно обобщить в следующей форме.
При построении моделей обычно рассматривается некоторая эмпирическая ситуация Е, которую можно воспринимать органами чувств (в нашем примере это было движение тела по плоской поверхности). Ситуация Е обычно может быть охарактеризована некоторым набором характеристик х1, х2, …, хn, например, это сила трения F и расстояние R в примере с телом. Ситуацию Е вместе с ее характеристиками х1, х2, …, хn обозначим в виде Е(х1, х2, …, хn). Далее можно представить последовательность ситуаций Е1, Е2, Е3, …, получаемые на основе изменений по крайней мере ряда характеристик ситуаций. Значения характеристик х1, х2, …, хn для ситуации Еi, где i = 1, 2, 3, …, можно обозначить через хi1, хi2, …, хin, и записать i-тую ситуацию в виде Еi = Е(хi1, хi2, …, хin). В этом случае может оказаться, что можно перейти к пределу по крайней мере для ряда характеристик, т.е. существуют пределы 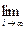 (xij) = xj, где j = 1,2,…,n. Тогда можно было бы определить некоторую предельную ситуацию E¥, получаемую из Ei на основе перехода к пределу характеристик этих ситуаций. Мы могли бы записать в этом случае
(xij) = xj, где j = 1,2,…,n. Тогда можно было бы определить некоторую предельную ситуацию E¥, получаемую из Ei на основе перехода к пределу характеристик этих ситуаций. Мы могли бы записать в этом случае
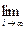 Еi = E(
Еi = E(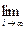 (хi1), …,
(хi1), …, 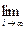 (хin)) = E¥
(хin)) = E¥
предельная ситуация E¥ получается как результат перехода к пределу характеристик до-предельных ситуаций.
Модель – это и есть как правило такого рода предельная ситуация E¥, полученная на основе тех или иных предельных переходов параметров эмпирических ситуаций. Переход к пределу при построении моделей обычно называется процедурой идеализации. Заметим, что здесь мы предлагаем модель самой модели, так что сами также используем некоторую идеализацию.
Из описанной концепции построения модели как предельной идеализации вытекает ряд следствий.
1. Если до-предельные ситуации Еi обычно принадлежат эмпирической реальности и могут восприниматься органами чувств, то их предел E¥ как таковой в эмпирической реальности уже не встречается и принадлежит сфере теоретического познания (отсюда и название «идеализация», т.е. утверждение чего-то идеального, что в таком виде в чувственной реальности не встречается).
2. В то же время предельная ситуация E¥ и не совершенно не связана с эмпирическими ситуациями Еi. E¥ выступает именно как предел эмпирических ситуаций, в связи с чем в эмпирических ситуациях присутствует тенденция такого их изменения, в которой они могут все более и более приближаться к предельной ситуации, как бы все лучше воспроизводя ее в себе.
Трудность и своеобразие понимания моделей в научном познании – это и есть во многом результат своеобразного положения предела по отношению к своим до-предельным значениям. Предел, с одной стороны, не есть ни одно из до-предельных значений, - и в этом выражен момент отличия моделей от моделируемой ими реальности. Но, с другой стороны, предел предельно связан с до-предельными значениями, выражая себя в них как предельная тенденция, как возможность этих значений все более приближаться к пределу и все более ярко выражать его в себе - в этом выражен момент связи моделей и моделируемой реальности.
Здесь, правда, можно было бы задать и такой вопрос – а зачем вообще нужны такие непростые процедуры построения моделей? Нельзя ли как-то более непосредственно познавать то, что мы воспринимаем органами чувств?
Вряд ли, конечно, можно предложить такой же простой ответ на этот вопрос, но, по крайней мере, можно было бы заметить, что человеческий разум, по-видимому, не способен прямо познать эмпирическую реальность, он постоянно нуждается в разного рода пределах-идеализациях для понимания этой реальности. По-видимому, сам разум принадлежит некоторой иной реальности, и модели – это результат своего рода компромисса между природой разума и эмпирическим, материальным миром. В моделях-пределах разум как бы тянет материю выйти из себя, но выйти изнутри нее самой, - словно в самой материи заключена возможность выхода из нее по направлениям ее пределов. Уже достаточно долгая история успешности применения метода моделирования в научном познании говорит так же о том, что такой компромисс материи и идеи достаточно плодотворен.
Модель проще и идеальней эмпирических ситуаций – и в этом выигрыш для чистого разума, который вообще ощущает себя лучше в мире простых и идеальных сущностей. Но модель одновременно ухватывает из объекта некоторую его сторону-тенденцию, и не совершенно чужда объекту. Скорее модели выражают роли объектов, которые объекты могут начинать играть в некоторых более идеальных ситуациях, приближаясь к пределу модельности.
Наконец, возможен механизм компенсации избыточной идеализации, заложенный в слишком упрощающих моделях. Модели можно усложнять, как бы складывая между собою разные модели одного объекты и получая модели-суммы, которые ближе к полной природе объекта, чем отдельные модели-слагаемые. Развитие научного познания – это во многом образование таких моделей-сумм из множества частных моделей. Теперь объект оказывается пределом бесконечной суммы отдельных моделей. Так мы имеем дело с двумя пределами:
1. Предел выделяющий - При построении частных моделей переход к пределу очищает объект ото всех иных его ролей.
2. Предел восполняющий - При суммировании частных моделей переход к пределу, наоборот, начинает восполнять модели до объекта. Здесь разум начинает возвращение к материальному миру, но уже на новом уровне его умного бытия.
§ 2. Модели и интервал моделируемости
Переход к пределу – важная, но не единственная операция, используемая при построении модели. Еще одна такая операция – отвлечение от ряда свойств моделируемого объекта. Например, при моделировании наиболее оптимальной формы самолета можно отвлечься от материала, из которого будет сделана эта форма. При моделировании газа можно отвлечься от конкретного вида его молекул, представляя их просто как малые материальные тела. Во всех таких случаях происходит обеднение объекта, и ряд проявлений объекта просто отбрасываются, считаясь несущественными для решения поставленной задачи.
Еще одна мыслительная операция, используемая при построении моделей, - создание некоторых новых свойств, которые невозможно наблюдать в эмпирической реальности. В этом случае модель оказывается богаче чувственного образа моделируемого объекта. Предполагается, что объект может содержать нечто такое, что невозможно наблюдать органами чувств, и такие состояния также могут использоваться при построении модели. Образование новых характеристик или объектов может происходить, как мы видели, уже при переходе к пределу последовательности эмпирических ситуаций (новыми свойствами здесь были нулевая сила трения и вечное движение объекта). Но в общем случае новые свойства или объекты могут использоваться в модели и помимо предельного перехода. Например, чувственный образ может быть представлен как часть некоторого целого, которое уже нельзя вполне наблюдать органами чувств. Если один и тот же эмпирический объект Х в одних и тех же условиях может вести себя по-разному, то можно предполагать наличие некоторого «скрытого параметра» У, который связан с Х и может обладать разными состояниями, приводя к разному поведению Х. Построение модели Х может быть связано в этом случае с гипотезой о существовании прямо ненаблюдаемого У. Например, можно предположить существование черной дыры в некоторой области космического пространства на основании стягивания к этой области космического газа. Или предположить, что в сознании человека возникла какая-то новая идея, если он внезапно изменил свое поведение.
В итоге на основе тех или иных операций возникает некоторый новый объект – модель, и наука начинает далее работать с этим объектом. Модель должна отвечать следующим требованиям:
1. Модель должна обнаруживать некоторое сходство с объектом.
2. Благодаря этому сходству, мы можем вместо объекта исследовать модель, как бы замещая объект моделью.
В общем случае можно говорить о некоторой системе условий, в рамках которой достигается отождествление объекта и модели. Будем называть эту систему условий интервалом моделируемости. Например, представление материального тела точкой возможно только в том случае, когда либо размеры тела сравнительно малы с масштабом процесса, либо в каждой точке движение тела одинаково. Система таких условий представляет из себя интервал точечной моделируемости, т.е. интервал моделируемости для такой модели, как точка. Представление реального газа моделью идеального газа возможно лишь в случае, когда можно пренебречь взаимодействием молекул газа. Это интервал моделируемости для модели идеального газа. Модель абсолютно черного тела применяется в случае, когда можно пренебречь количеством отраженного от объекта света, сравнительно со светом поглощенным, - таков интервал моделируемости в этом случае.
Пусть О – моделируемый объект, И – интервал моделируемости, М – модель, имеющая смысл в этом интервале. Мы можем отождествить объект и модель в рамках интервала моделируемости. Запишем это утверждение в следующем виде: (О = М)¯И – объект О равен модели М при условии интервала моделируемости И. Стрелочка ¯ в выражении Х¯У может читаться как «Х-при-условии-У». В записи (О = М)¯И рассматривается условное отношение равенства между объектом и моделью, т.е. не вообще равенство, а равенство лишь в некоторой системе условий, в данном случае – в рамках интервала моделируемости. Такое равенство можно понимать как просто равенство, но уже не между объектом и моделью, а между моделью и объектом, взятом в рамках интервала моделируемости. Таким образом, (О = М)¯И можно понимать как О¯И = М¯И – равенство между О¯И – объектом, рассматриваемом в интервале моделируемости, и М¯И – моделью, рассматриваемой в том же интервале. Однако интервал моделируемости входит в определение самой модели М, так что мы могли бы записать: М = М¯И – модель-в-интервале-И есть просто модель М. Тогда равенство О¯И = М¯И переходит в равенство О¯И = М, т.е. модель есть один из аспектов объекта, одна из его сторон или ролей, выделяемая из объекта в рамках интервала моделируемости. Эта сторона и обозначается как О¯И – объект-при-условии-И. Следовательно, отношение объекта и модели – это отношение объекта О и одного из его аспектов О¯И, - вот почему модель и не вполне совпадает с объектом, и не вполне отлична от него. Рассматривая различные интервалы моделируемости И1, И2, …, Иn, можно выделять разные аспекты объекта, О¯И1, О¯И2, …, О¯Иn, как разные его модели М1 = О¯И1, М2 = О¯И2, …, Мn = О¯Иn. Например, человека можно моделировать как некоторый физический объект, как биологический или социальный объект, выделяя в нем разные аспекты его существования как его модели.
Условное равенство объекта и модели в рамках интервала моделируемости можно называть отношением заместительной репрезентации объекта моделью – модель как бы замещает объект, вполне представляя (репрезентируя) его в рамках интервала моделируемости. Обычно от этого отношения требуется еще одно замечательное свойство. Требуется, чтобы равенство между объектом и моделью сохранялось и в рамках некоторых преобразований, производимых над моделью. Если мы воздействуем на модель и получаем какое-то новое состояние модели, то нам хотелось бы быть уверенными, что новое состояние модели окажется одновременно и новым состоянием моделируемого объекта. Здесь отношение заместительной репрезентации должно распространиться не только на какое-то одно статическое состояние модели, но и на некоторые переходы модели из одного состояния в другое.
Пусть m и m* - разные состояния одной модели М, а t – преобразование, переводящее состояние m в состояние m*, т.е. t(m) = m*. С другой стороны, пусть о, о* - состояния объекта, которые могут быть смоделированы состояниями m и m*, и Т – преобразование, образующее состояние о* из состояния о, т.е. Т(о) = о*. В этом случае динамическая моделируемость объекта могла бы быть выражена в форме
(Т(о) = о*)¯И есть то же, что t(m) = m*,
т.е. преобразование состояний объекта Т(о) = о*, рассмотренное в рамках интервала моделируемости И, есть то же самое, что преобразование состояний модели t(m) = m*. Условное равенство (Т(о) = о*)¯И мы, как и прежде, можем рассмотреть как равенство условных состояний и преобразований объекта: Т¯И(о¯И) = о*¯И – условное преобразование Т¯И действует на условное состояние объекта о¯И и образует другое условное состояние о*¯И. Везде в качестве системы условий здесь выступает интервал моделируемости И. Теперь, сравнивая два выражения, Т¯И(о¯И) = о*¯И и t(m) = m*, мы могли бы сделать тот вывод, что условное преобразование Т¯И есть модельное преобразование t, а условные объектные состояния о¯И и о*¯И есть состояния модели m и m*. Так свойство моделируемости дифференцируется и распространяется на состояния объекта и модели, и преобразования объекта и модели.
В этом случае мы можем заменить познание объектных преобразований исследованием преобразований над моделью. Это особенно важно, если достичь требуемых преобразований объекта Т(о) = о* по какой-либо причине бывает сложно или даже невозможно. Например, если требуется изучить, что может произойти с человеком в автомобиле при той или иной аварии, можно использовать манекен как модель человека, изучая последствия столкновения на манекене и затем перенося их на человека. Или можно использовать модель самолета, изучая ее реакцию на те или иные предельные нагрузки, грозящие разрушением самолета. Если же мы имеем дело с далекой звездой, то можно построить математическую модель протекающих на ней процессов и исследовать конкретные сценарии их протекания, перенося результаты этого исследования на сам объект. Во всех этих случаях не просто строится статическая модель объекта, но эта модель подвергается тем или иным воздействиям и образует свои новые состояния, которые также рассматриваются как модели соответствующих состояний объекта.
§ 3. О некоторых видах моделей
В этом параграфе мы остановимся на рассмотрении некоторых видов моделей, используемых в научном познании.
Можно говорить, например, о материальных и мыслительных моделях. Модель корабля, сделанная из пластмассы, - это его материальная модель. Чертеж корабля или уравнения, описывающие элементы формы, – это мыслительные модели. Мыслительные модели можно также подразделять на образные и символические. Образные модели сохраняют элемент сходства формы модели и объекта – таков, например, чертеж корабля. Символические модели такого сходства уже не содержат. Таковы, например, различные математические уравнения, описывающие те или иные структуры или процессы.
Одним из довольно распространенных видов моделей являются модели типа «черного ящика». При построении таких моделей не интересуются внутренней структурой моделируемого объекта, но только его функцией или поведением. Объект в этом случае моделируется как система, на вход которой поступают разного рода стимулы S, а на выходе система реагирует на эти стимулы различными реакциями R. В итоге система моделируется как некоторое правило F, которое ставит в соответствие определенным стимулам S определенные реакции R. Кратко это можно записать таким образом: R = F(S) – R есть результат правила F, примененного к S. На основе какой внутренней структуры объекта достигается это преобразование – этим в данном случае не интересуются. Внутренняя структура объекта рассматривается как «закрытая» для процесса познания, - как некоторый «черный ящик», в который предпочитают не заглядывать. Момент независимости функции от структуры, возможность воспроизвести одну и ту же функцию при разных структурах - это и есть интервал моделируемости для такого рода функциональных моделей. Одним из наиболее ярких примеров таких моделей являются модели человека в бихевиоризме – одном из направлений психологии (название «бихевиоризм» происходит от англ. «behaviour» - «поведение»). Психика, внутренний мир человека рассматривается в этом случае как «черный ящик», содержимое которого недоступно для научного познания. Человек представляется как некоторая функция F, которая связывает определенные стимулы с определенными реакциями. Например, у человека Х чувство голода (S) может вызывать раздражительность (R1), а у человека У – заторможенность (R2). Тогда человека Х можно представить как функцию F1, где F1(S) = R1, а человека У – как функцию F2, где F2(S) = R2. Промежуточная инстанция в виде особенностей психики или биологии здесь просто опускается и не рассматривается. Хотя эти модели могут показаться слишком жесткими, но и для них существуют свои интервалы моделируемости, в рамках которых они имеют смысл и могут быть применимы. Подобный же подход используется при моделировании сознания и мышления человека на компьютерах. Здесь ставится задача создать такой компьютер, который на те же стимулы давал те же реакции, что и человек, и неважно, что у человека это достигается на основе биологической структуры его тела, а у компьютера - на неорганических элементах его устройства. Главное здесь – моделирование поведения и функции, независимо от того, на какой конкретной структуре будет построена такая модель поведения.
Противоположным типом моделей являются модели по типу «белого ящика», когда, наоборот, все внимание исследователя направляется на моделирование внутренней структуры объекта, независимо от того, какую функцию совершает эта структура. В этом случае считается возможным принять в качестве модели и такую структуру, которая не могла бы выполнять функции моделируемой структуры. Момент независимости структуры от функции – интервал моделируемости для такого рода моделей. Например, структура живых организмов может моделироваться в этом случае в разного рода неорганических моделях – таковы разного рода муляжи органов и частей тела, которые применяются в медико-биологическом образовании.
Обобщением моделей по типу «черного» и «белого ящиков» являются разного рода математические модели, представляющие из себя различные примеры математических структур. При построении таких моделей важнейшим понятием является понятие изоморфизма математических структур, о котором мы уже упоминали выше. Здесь нужно специально заметить, что понятие математической структуры не совпадает с понятием структуры материального объекта. В форме тех или иных математических структур можно выражать как материальные структуры, так и материальные функции и процессы. Вот почему математические модели являются наиболее универсальными средствами моделирования в современной науке.
В рамках интервала моделирования И моделируемый объект О предстает как модель М, где М = О¯И. Равенство = в этом отношении теперь можно понимать в смысле изоморфизма структур М и О¯И. Сам объект О превышает свой аспект О¯И и может быть представлен как более богатая структура, по отношению к которой модель О¯И выступает как под-структура – часть этой более богатой структуры. Построение различных моделей одного объекта предстает в этом случае как построение различных под-структур бесконечно богатой структуры объекта, которая, по-видимому, вполне никогда не сможет быть смоделирована.






