| Вычисления в Excel | Вычисления в MathCad | |
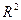
| 0,992 | 0.992 |
При верном вычислении значения коэффициентов, вычисленные в Excel должны совпадать с вычислениями в MathCad.
3. ПРОВЕДЕНИЕ РАСЧЁТОВ СТАНДАРТНЫМИ СРЕДСТВАМИ MICROSOFT EXCEL 2003 ДЛЯ ПОСТРОЕНИЯ АППРОКСИМИРУЮЩИХ ЗАВИСИМОСТЕЙ
Введем данные таблицы 1 в Microsoft Excel 2007 (Таблица П.1.1).
Построим график функции эмпирических значений (Рис. 1).
Выделив одним нажатием левой кнопки мыши график — открыть контекстное меню и выбрать пункт Добавить линию тренда (Рис. 11). В появившимся окне (Рис. 12) выбрать необходимую аналитическую зависимость и указать пункты; показывать уравнение на диаграмме; поместить на диаграмму величину достоверности (
).
Рис. 11 Контекстное меню графика функции в Excel
Рис. 12 Формат линии тренда в Excel
Рис. 13 Графики линии тренда в Excel
Сравним значения коэффициентов аппроксимирующих функций и коэффициентов детерминированности с уже ранее рассчитанными значениями по формулам наименьших квадратов в Excel и MathCad.
Таблица 6
Сравнение вычислений коэффициентов функций и коэффициентов детерминированности с Excel и MathCad
| Вычисления в Excel | Вычисления в MathCad | Вычисления стандартными средствами Excel | |
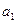
| 1,079 | 1.079 | 1,079 |
| -0,001 | -1.353*10^(-3) | -0,001 |
|
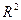
| 0,9147 | 0.915 | 0,944 |
|
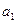
| 1,216 | 1.216 | 1,216 |
|
| -0,003 | -2.822*10^(-3) | - 0,002 |
| 0,000 | 2.854*10^(-6) | 3E-06 |
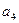
| 0,000 | -9.622*10^(-10) | -1E-09 |
|
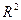
| 0,992 | 0.992 | 0,9922 |
Значения коэффициентов функций и коэффициентов детерминированности вычисленные в Excel и в MathCad совпадают с вычислениями стандартными средствами Excel.
Вывод
В данной курсовой работе были получены две аппроксимирующие функции, отображающие заданную эмпирическую зависимость — экспоненциальная и полиномиальная третьей степени. Расчет двумя способами и использование стандартных средств Excel показали одинаковые ответы (Таблица 6).
Рассмотрев два способа нахождения аппроксимирующих функций и проверив полученные результаты стандартными средствами Microsoft Excel 2003 можем сделать вывод, что вычисления с помощью метода наименьших квадратов в Excel и MathСad по сложности и затраченном времени примерно равны и выдают одинаковые результаты. Стоит отметить, что в MathСad решение выглядит нагляднее чем в Excel.
Исходя из полученных значений коэффициентов детерминированности (
; 
) — обе функции подходят для аппроксимации заданной эмпирической функции. Судя по коэффициентам детерминированности для аппроксимации лучше подходит полиномиальная функция, т.к. ее коэффициент детерминированности ближе к единице чем у экспоненциальной, но исходя из того что значения первых двух коэффициентов обоих функций примерно равны, то можно сделать вывод о том, что скорее всего изначальная зависимость плотности сухого воздуха от температуры экспоненциальная.
Приложение
Таблица. П. 1.1
Таблица. П. 1.2
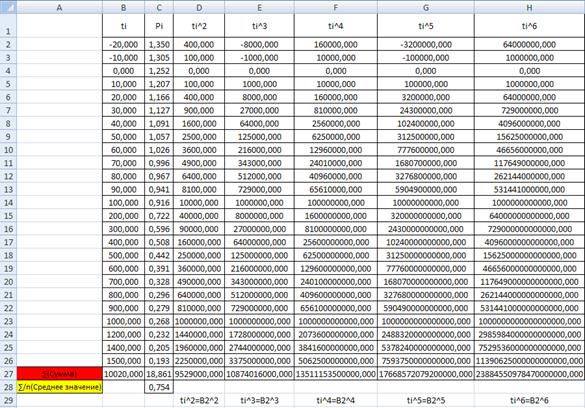
Таблица. П. 1.3
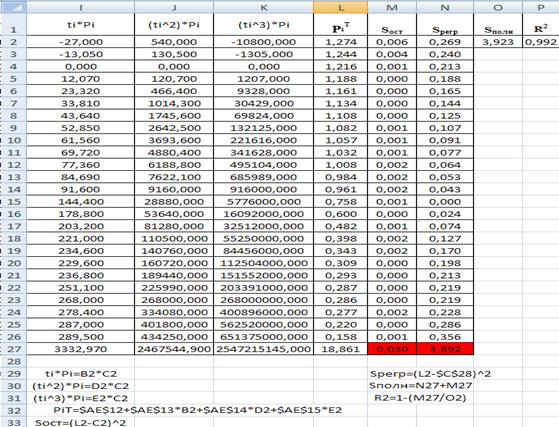
Таблица. П. 1.4.
Таблица. П. 2.1
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
1. Информатика. Методические указания к курсовой работе для студентов специальностей 170100 и 170300 / А. П. Кондрашев. СПб, 2002.
2. Информатика: Учебник / Под ред. Проф. Н. В. Макаровой. М., Финансы и статика 1997.
3. Информатика. Практикум по технологии работы на компьютере / Под ред. проф. Н. В. Макаровой. М., Финансы и статика 1997.
