Элементы теории корреляции

КУРСОВАЯ РАБОТА

По дисциплине:

Информатика

^{(наименование учебной дисциплины согласно учебному плану)}

Тема: Аппроксимация функции, отображающей зависимость плотности сухого воздуха от температуры.

ВЫПОЛНИЛ: студент гр. ГМ-07-1 ______________ / Ширшов В.А. /

^{(подпись)} ^(Ф.И.О.)

ОЦЕНКА: _____________

ДАТА: ___________________

ПРОВЕРИЛ: ст. преподаватель ___________ / Кондрашев А.П. /

^{(подпись) (Ф.И.О.)}

Санкт-Петербург

2008 год.

Аннотация

В работе используются: элементы теории корреляции, принципы построения эмпирических формул методом наименьших квадратов.

В процессе выполнения курсовой работы, тремя способами (в Microsoft Excel 2003, PTC MathCad 14 и стандартными средствами Microsoft Excel 2003, полученные при построении линии тренда) установлена теоретическая зависимость плотности сухого воздуха ρ от температуры t˚ C. Определена функция, наилучшим образом отображающая экспериментальные данные.

Результат работы – вид аналитической зависимости.

Работа включает: Страниц 26, таблиц 6, рисунков 14, приложений 5.

The summary

In work are used: elements of the theory of correlation, principles of construction of empirical formulas a method of the least squares.

In the course of performance of the course work, three ways (in Microsoft Excel 2003, PTC MathCad 14 and the standard means Microsoft Excel 2003, the lines of a trend received at construction) establish theoretical dependence of density of dry air ρ from temperature t˚ C. The function in the best way displaying experimental data is defined.

Result of work – a kind of analytical dependence.

Work includes: Pages 26, tables 6, drawings 14, appendices 5.

ОГЛАВЛЕНИЕ

Введение.. 4

1. ПРОВЕДЕНИЕ РАСЧЁТОВ В ТАБЛИЧНОМ ПРОЦЕССОРЕ MS EXCEL ИСПОЛЬЗУЯ МЕТОД НАИМЕНЬШИХ КВАДРАТОВ 11

1. 1. 1. РАСЧЕТ ЭКСПОНЕНЦИАЛЬНОЙ АППРОКСИМАЦИИ.. 11

1.1.2 РАСЧЕТ КОЭФФИЦИЕНТА ДЕТЕРМИНИРОВАННОСТИ.. 12

1.2.1 Расчёт полиномиальной апроксимации.. 13

1.2.2 РАСЧЕТ КОЭФФИЦИЕНТА ДЕТЕРМИНИРОВАННОСТИ.. 14

2. ПРОВЕДЕНИЕ РАСЧЁТОВ С ИСПОЛЬЗОВАНИЕМ МАТЕМАТИЧЕСКОГО ПАКЕТА PTC MATHCAD ИСПОЛЬЗУЯ МЕТОД НАИМЕНЬШИХ КВАДРАТОВ.. 15

2. 1. 1. РАСЧЕТ ЭКСПОНЕНЦИАЛЬНОЙ АППРОКСИМАЦИИ.. 15

2.1.2 РАСЧЕТ КОЭФФИЦИЕНТА ДЕТЕРМИНИРОВАННОСТИ.. 17

2.2.1 Расчёт полиномиальной апроксимации.. 17

2.2.2 РАСЧЕТ КОЭФФИЦИЕНТА ДЕТЕРМИНИРОВАННОСТИ.. 19

3. ПРОВЕДЕНИЕ РАСЧЁТОВ СТАНДАРТНЫМИ СРЕДСТВАМИ MICROSOFT EXCEL 2003 ДЛЯ ПОСТРОЕНИЯ АППРОКСИМИРУЮЩИХ ЗАВИСИМОСТЕЙ.. 20

Вывод.. 22

Приложение.. 23

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ... 26

Введение

Температура - величина, характеризующая степень теплового состояния тела (газа) или скорость хаотического движения молекул (чем выше температура, тем больше скорость их движения, и наоборот). Температуру воздуха можно измерять по двум шкалам: Цельсия и абсолютной шкале Кельвина. За нуль градусов по шкале Цельсия принято считать температуру таяния льда, а за 100° - температуру кипения воды при атмосферном давлении, равном 760 мм рт. ст.

Плотность воздуха - это количество воздуха, содержащегося в 1 м³ объема.В физике существует понятие двух видов плотности - весовая (удельный вес) и массовая. В аэродинамике чаще всего пользуются массовой плотностью. Весовая плотность (удельный вес) воздуха - это вес воздуха в объеме 1 м³. Обозначается буквой g.

Вес воздуха G - величина непостоянная и изменяется в зависимости от географической широты и силы инерции, возникающей от вращения Земли вокруг своей оси. На полюсах вес воздуха на 5% больше, чем на экваторе. Установлено, что 1 м³ воздуха при стандартных атмосферных условиях (барометрическое давление 760 мм рт. ст., t=+15°С) весит 1,225 кгс, следовательно, весовая плотность (удельный вес) 1 м³ объема воздуха в этом случае равна g=1,225 кгс/м³.

Массовая плотность воздуха - это масса воздуха в объеме 1 м³. Обозначается греческой буквой р. Масса тела - величина постоянная. За единицу массы принята масса гири из иридистой платины, хранящейся в Международной палате мер и весов в Париже.

Согласно закону Бойля-Мариотта плотность воздуха будет тем больше, чем больше давление, а согласно закону Гей-Люссака плотность воздуха тем больше, чем меньше температура воздуха. Объединив эти два закона для определения зависимости между плотностью, давлением и температурой воздуха, получим уравнение состояния газа (закон Бойля-Мариотта - Гей-Люссака) , где P- давление воздуха, V- объём воздуха, m-масса воздуха, M –молярная масса воздуха, R- газовая постоянная, T -температура воздуха. Преобразуя эту формулу получим уравнение нахождения его плотности . Отсюда ясно, что с повышением температуры плотность воздуха падает.

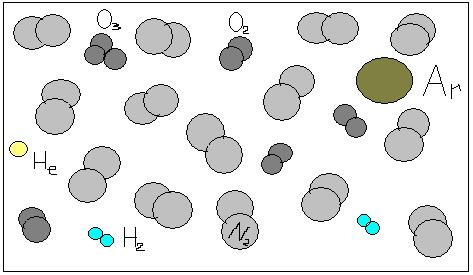
Рис.1. Воздух нижних слоёв атмосферы.

На представленном выше рисунке в простейшем виде показано состояние атмосферного воздуха в некотором его объёме. Атмосферный воздух состоит примерно на 70% из азота , на 21% из кислорода , примерно 8% приходится на водород, а всё остальное инертные газы: гелий , аргон и т.д. При понижении окружающей температуры молекулы разных газов становятся плотнее друг к другу, а при её повышении наоборот. Ниже представлена типичная зависимость плотности воздуха от температуры.


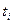
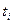
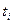
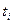
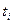
-20	1,350	1,127	0,967	0,508	0,279
-10	1,305	1,091	0,941	0,442	0,268
	1,252	1,057	0,916	0,391	0,232
	1,207	1,026	0,722	0,328	0,205
	1,166	0,996	0,596	0,296	0,193

Таблица1. Зависимость плотности сухого воздуха от температуры .

Одной из задач является отражение опытных данных выше представленной таблицы в некоторой зависимости одного параметра от другого через подходящую формулу. Используя табличный процессор Microsoft Office Excel, составив график по данной таблице, можно определить, что максимально подходящими функциями являются экспоненциальная и полиноминальная(третьей степени). Следующий шаг- - их аппроксимация..

Аппроксимация (от латинского “approximate”- приближаться) – приближенное описание эмпирических данных с помощью уравнений.

Для аппроксимации экспоненциальной функции мы воспользуемся методом наименьших квадратов.

Необходимо решить задачу - найти эмпирическую формулу

P^Т =F (

_,a₁,a₂,..a_m),

(1)

где a₁,a₂,..a_m - коэффициенты. Вид функции и значения коэффициентов a₁,..a_mподбираются таким образом, чтобы значения P^Т_i, вычисленные по эмпирической формуле при различных значениях t__i, возможно мало отличаться бы от опытных значений P_i.

Каждая пара чисел ( __i_,P_i₎ из исходной таблицы 1 определяет точку M_i на плоскости XOY. Используя формулу (1) с различными значениями коэффициентов a₁, a₂,..a_m, можно построить множество кривых, которые будут являться графиками теоретических функций P^Т.

Согласно методу наименьших квадратов наилучшими коэффициентами a₁,a₂,..a_m считаются те, для которых сумма квадратов отклонений найденной теоретической функции от заданных эмпирических значений будет минимальной. Следовательно, задача состоит в определении коэффициентов a₁, a₂,..a_m (т. е. в выборе одной кривой из множества), таким образом, чтобы сумма квадратов отклонений была наименьшей.

(2)

Для того чтобы найти набор коэффициентов a₁,a₂,..a_m, при которых достигается минимум функции S, определяемой формулой (2), используем необходимое условие экстремума функций нескольких переменных – равенство нулю частных производных. В результате получим нормальную систему для определения коэффициентов a₁ (i =1, 2, …m).

Таким образом, нахождение коэффициентов a_i, сводится к решению системы:

(3)

В качестве эмпирической зависимости берут функцию, в которую неопределенные коэффициенты входят нелинейно. При этом функцию выбирают, как правило, такого вида, чтобы можно было ее линеаризовать, т.е. свести к линейной. К числу таких зависимостей относится и экспоненциальная .

В данных зависимостях a₁ и a₂ являются коэффициентами, которые необходимо численно определить.

В обоих случаях линеаризация достигается путем логарифмирования. В результате получим соотношения:

	(4)
	(5)

Конкретный вид системы (3) зависит от того, из какого класса эмпирических формул мы ищем зависимость (1). В случае линеаризованной экспоненциальной зависимости система (3) примет вид:

(6)

Во многих случаях в качестве эмпирической зависимости берут функцию, выражающую линейную, квадратичную или полиноминальную более высоких степеней зависимость одной переменной от другой.

В случае полиноминальной зависимости третьей степени (кубической) система (3) примет вид:

(7)

Данные системы могут быть решены любым известным способом (методом Гаусса, методом итерации, по формулам Крамера и т. д.), но мы будем решать их матричным методом.

ЭЛЕМЕНТЫ ТЕОРИИ КОРРЕЛЯЦИИ

Чтобы выяснить насколько точно построенная кривая отражает эмпирические данные, вводится еще одна характеристика - коэффициент детерминированности. Поясним подробно, что означает этот коэффициент и как он определяется.

Напомним, что вычисленные по эмпирической формуле при каждом значении t_iзначения P_i^T, обычно, называют теоретическими, в отличие от исходных, эмпирических данных P _i.

Вычислим сумму квадратов отклонений теоретических значений функции от эмпирических данных, обозначив эту сумму S_ост.

(8)

Полученная величина характеризует отклонение теоретических результатов от экспериментальных данных. Чем больше S_ост, тем хуже выбранная теоретическая функция описывает экспериментальные данные и, наоборот, чем меньше S_ост, тем лучше выбранная функция описывает экспериментальные данные.

Введем понятие регрессионной суммы квадратов:

(9)

Эта величина S_регр характеризует разброс теоретических данных относительно среднего значения.

В теории корреляции доказано следующее равенство:

(10)

Обозначим: , тогда, очевидно, справедливо следующее равенство:

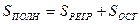
(11)

Коэффициент детерминированности R² определяется по формуле:

(12)

Чем меньше остаточная сумма квадратов по сравнению с полной суммой квадратов, тем больше значение коэффициента детерминированности R², который показывает, насколько хорошо полученная теоретическая функция описывает взаимосвязь между эмпирическими данными. Если коэффициент детерминированности равен 1, то имеет место полная корреляция фактических данных с выбранной теоретической моделью. В противоположном случае, если коэффициент корреляции близок к нулю, то уравнение регрессии выбрано неудачно и не может использоваться для вычисления значений функции.

1. ПРОВЕДЕНИЕ РАСЧЁТОВ В ТАБЛИЧНОМ ПРОЦЕССОРЕ MS EXCEL ИСПОЛЬЗУЯ МЕТОД НАИМЕНЬШИХ КВАДРАТОВ