Обработка результатов тестирования методами современной теории тестов IRT

Материалы для самостоятельного изучения:

 

Вычисления рекомендуется выполнять в электронных таблицах

Основная суть IRT - переход от наблюдаемых характеристик к скрытым (латентным) путем ряда преобразований. Если воспользоваться терминами классической теории тестов, то это переход от наблюдаемых результатов (баллов) к истинным.

Современная теория тестов имеет ряд ограничений в применении. Прежде всего она не работает на маленьких выборках (для IRT выборка должна быть не менее 1000 человек). IRT не будет работать на результатах «сырых» тестов, так как в основе ее применения лежат абсолютные математические модели. Современная теория применима для работы на репрезентативных выборках и на калиброванных заданиях. Одно из важных условий - распределение результатов по нормальному закону.

Соотношение двух параметров (тета-уровень подготовленности и бета-трудность задания) датский математик Г.Раш предложил ввести в виде разности 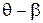, исходя из предположения, что эти параметры оцениваются в одной и той же шкале. Абсолютная величина разности 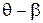- это расстояние, на котором находится испытуемый с уровнем подготовки , от задания с трудностью .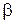

При

 

При

 

При

 

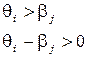
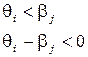
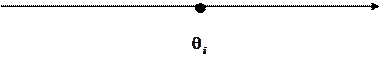
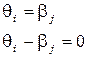
Если эта разность велика по модулю и меньше нуля, то это значит, что уровень подготовки намного ниже трудности задания (такое задание не имеет смысла использовать для измерения уровня подготовленности такого испытуемого, так как с очень большой вероятностью он сделает его неверно). Большие положительные значения разности также говорят о несоответствии уровня подготовленности и трудности задания, но в другую сторону, и соответственно такое задание тоже нельзя использовать для процесса контроля или обучения.

 

 

Задание 1. Имея начальные данные в таблицах провести оценку параметров 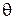и 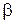и вычислить ошибку измерения по однопараметрической модели используя алгоритм расчета параметров 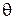и 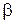для однопараметрической модели.

 

Алгоритм расчета параметров 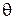и 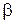для однопараметрической модели

1. Подсчет долей правильных и неправильных ответов каждого испытуемого на все задания теста.

Доля правильных ответов p_i = X_i / n, где n -число заданий теста.

Доля неправильных ответов q_i = 1 - p_i

2. Производится предварительная оценка значений параметра, характеризующего уровень подготовки учеников.

Начальное значение параметра измеряется в логитах (логит - это единица измерения шкалы, на которой находятся и 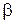) и находится по формуле:

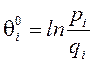
Начальные значения логитов уровня подготовки испытуемых

 

i	x	Доля правильных ответов i-го испытуемого pi	Доля неправильных ответов i-го испытуемого qi	Начальные оценки уровня подготовки в логитах
		0,4
		0,9
		0,1
		0,5
		0,6
		0,4
		0,5
		0,2
		0,5
		0,6

 

 

3. Доля правильных (p_j) и неправильных (q_j) ответов на каждое задание теста.

P_j = R_j/N, q_j = 1 - p_j, где R_j - количество правильных ответов на j-е задание теста, N - число испытуемых.

4. Начальная оценка параметра трудности задания находится по формуле

Начальные значения логитов трудности заданий

 

j	Rj	Доля правильных ответов на j-ое задание	Доля неправильных ответов на j-ое задание	Начальные оценки трудности заданий в логитах
		0,9
		0,8
		0,7
		0,6
		0,6
		0,5
		0,4
		0,3
		0,2
		0,1

 

Теоретически начальные значения параметров и 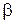могут меняться в интервале от минус бесконечности до плюс бесконечности. Но практически при 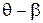<-5 значения вероятности (Р) близки к 0. Когда 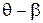>5, тогда вероятность очень близка к 1. Практически на шкале логитов используется интервал от -3 до 3 (-4 до 4).

5.Подсчитываются средние значения логитов уровня подготовленности и логитов трудности заданий теста.

 

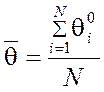
6. После завершения пятого этапа оценки каждого из параметров тета и бета выражены в интервальной шкале, но с разными значениями средних и разными стандартными отклонениями. Далее начальные значения логитов уровней подготовленности трудности заданий теста переводятся в единую шкалу интервальных оценок. Стандартизация достигается с помощью ряда специальных преобразований, для осуществления которых вычисляются:

n дисперсия по множеству значений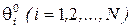

n дисперсия по множеству

n поправочные коэффициенты

Оценки параметров и 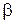в единой интервальной шкале находятся по

Две последние формулы очень важны, так как позволяют преодолеть ряд существенных недостатков классической теории тестов, с их помощью можно получить объективные оценки параметров испытуемых и заданий, не зависящие друг от друга и выраженные в единой интервальной шкале.

7. Оценивается стандартная ошибка измерения S_e от , которая вычисляется для каждого значения .

8. Стандартная ошибка измерения S_e от 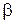, которая вычисляется для каждого значения .

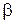9. Метод максимального правдоподобия для уточнения параметров и .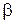

После подсчета значений параметров 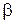и в шкале логитов приступают к построению характеристических кривых заданий теста. Анализ их взаимного расположения позволяет наметить пути дальнейшего совершенствования теста и сформировать систему заданий, наиболее эффективных для уровня подготовки каждого испытуемого выборки.

Процесс совершенствования теста начинается с удаления лишних заданий, нарушающих нормальный характер распределения значений бета. Далее разработчику необходимо обратить внимание на случаи наложения характеристических кривых и избавиться от лишних заданий, которые ничего не дают для теста как совокупности работающих заданий возрастающей трудности.

Следующий важный шаг при коррекции теста связан с выделением «пустых» интервалов оси , где нет характеристических кривых. В тест необходимо добавить задания. Соответствующие по трудности выделенным интервалам на оси латентной переменной . В идеале характеристические кривые должны заполнять более менее равномерно практически весь интервал (- 5; 5) шкалы логитов. Причем заданий средней трудности должно быть намного больше, чем на краях распределения.

Для более обоснованного решения включения или удаления предтестовых заданий необходим дополнительный анализ тестируемого контингента. Если группа гомогенна по уровню подготовки и большинство значений расположено на небольшом интервале оси латентной переменной, то основную часть заданий следует сгруппировать на этом интервале, расположив характеристические кривые достаточно плотно. В случае гетерогенной по подготовке выборки испытуемых значения параметра трудности должны охватывать больший интервал на оси , а характеристические кривые заданий могут быть расположены довольно далеко друг от друга.

 

Задание 2. В таблице даны оценки параметров шести заданий, полученных по современной теории тестов.

Задание	Трудность(β)	Диф. Способность (а)	Угадывание (с)
	1.0	1.5	0.00
	1.0	0.6	0.00
	0.7	1.8	0.10
	-0.5	1.3	0.20
	0.5	1.0	0.00
	0.0	0.5	0.25

1.1 Для каждого задания вычислите по однопараметрической модели Р (θ) для θ = -3; -2; -1; 0; 1; 2; 3. Постройте графики характеристических кривых шести заданий.

1.2 Для каждого задания вычислите по двухпараметрической модели Р (θ) для θ = -3; -2; -1; 0; 1; 2; 3. Постройте графики характеристических кривых шести заданий

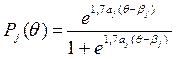
1.3 Для каждого задания вычислите по трехпараметрической модели Р (θ) для θ = -3; -2; -1; 0; 1; 2; 3. Постройте графики характеристических кривых шести заданий

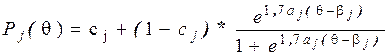
Ответьте на вопросы:

1). Какое задание самое легкое, самое трудное?

2). Какое задание из шести имеет наименьшую (наибольшую) дифференцирующую способность?

3). Какое из шести заданий для испытуемого с уровнем подготовленности θ = -1 имеет наибольшую вероятность правильного ответа? Какова вероятность для данного испытуемого выполнить это задание неверно - Q (θ)?

 

Задание 3. Вероятность правильного ответа Р (θ)для трех заданий при определенных величинах θ дана в таблице. Постройте харахтеристические кривые этих заданий.

 

Вероятность правильного ответа Р (θ) при определенных величинах θ для трех заданий дана в таблице. Постройте харахтеристические кривые трех заданий. θ	-3.0	-2.5	-2.0	-1.5	-1.0	-0.5		0.5	1.0	1.5	2.0	2.5	3.0
Зада
ния
	0,00	0,01	0,02	0,04	0,07	0,13	0,22	0,36	0,52	0,68	0,81	0,90	0,93
	0,00	0,00	0,01	0,04	0,13	0,30	0,54	0,79	0,93	0,98	0,99	0,99	0,99
	0,10	0,10	0,11	0,12	0,13	0,14	0,15	0,20	0,32	0,44	0,60	0,80	0,88