Рассмотрим совокупность условий
a 11 x 1 +... + a 1n x n = b 1,
a 21 x 1 +... + a 2n x n = b 2,
........................ ()
a m1 x 1 +... + a mn x n = b m,
где aij , bi - числа, а xj - буквы. Совокупность этих условий называется системой линейных уравнений относительно неизвестных x 1,..., x n. Последовательность чисел r 1 ,..., r n называется решением системы (), если при подстановке этих чисел вместо соответствующих неизвестных получаем истинные равенства. Систему уравнений называют совместной, если она имеет хотя бы одно решение. В противном случае ее называют противоречивой. Совместную систему уравнений называют определенной, если она имеет единственное решение. Если система уравнений имеет более одного решения, то систему называют неопределенной. Вводя матрицы
A =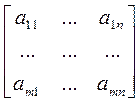 
, x = 
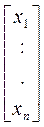, b =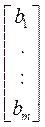 
систему () можно записать в матричной форме
A x = b. ()
Матрица А называется матрицей системы, а матрица
B =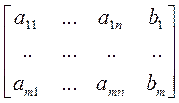 
называется расширенной матрицей системы. Вводя в рассмотрение вектора
a 1 =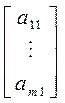 
,..., a n =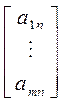 
систему () можно записать в векторной форме
x 1 a 1 +... + x n a n = b.
Система линейных уравнений называется крамеровской, если число уравнений совпадает с числом неизвестных и определитель матрицы системы отличен то нуля.
Рассмотрим методы решения таких систем.
В §3 мы отмечали, что в этом случае квадратная матрица А имеет обратную. Следовательно, можно умножить обе части равенства () слева на А- 1. В результате этой операции получим
x = A- 1 b. ()
Обратно, умножая соотношение () слева на А получим (). Таким образом, условия (), () равносильны, и поэтому формулу () можно рассматривать как формулу, решающую крамеровскую систему линейных уравнений. Для матрицы А существует только одна обратная матрица, следовательно, каждая крамеровская система имеет одно и только одно решение.
Формула () показывает, что неизвестное xi можно получить умножением i-ой строки матрицы А- 1 на столбец b. Отсюда, воспользовавшись формулой () из §3, получим
xi =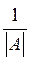 
(ï A ç i1b1 +... + ï A ê nibn)
или, в окончательной форме,
xi =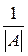 
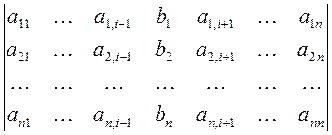(i = 1,..., n) ()
Формулы () называются формулами Крамера в честь математика середины прошлого столетия, в работе которого они впервые появились.
Пример.
x1 - x2 + 2x3 = 7
2x1 + x2 + 3x3 = 4
4x1 + 2x2 + x3 = 3
Для нахождения решения по формулам Крамера нужно вычислить определители
D =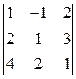 
, D 1 = 
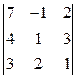, D 2 = 
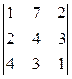, D 3 =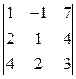 
Чтобы вычислить определитель D, вычитаем из 2-й и 3-й строки матрицы определителя первую строку, умноженную соответственно на 2 и 4. В результате получим
D =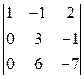 
= 1´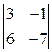 
= - 21 + 6 = 15.
Аналогично получаем, что D 1 = 30, D 2 = -45, D 3 = 15. Используя формулы Крамера, находим
x1 =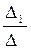 
= 2, x2 = 
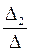= -3, x3 = 
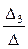= 1.
Формулы Крамера дают решение системы линейных уравнений через коэффициенты этих уравнений, но для фактического нахождения решений по формулам () требуется выполнить большое число вычислительных операций. Более экономичными с вычислительной точки зрения являются методы последовательного исключения неизвестных. Один из них, надлежащим образом упорядоченный, называется методом Гаусса.
Итак, рассмотрим крамеровскую систему линейных уравнений
a11x1 + a12 x2 +... + a1n xn = b1
a21x1 + a22 x2 +... + a2n xn = b2
.......................... ()
an1 x1 + an2 x2 +... + ann xn = bn
Без ограничения общности можно считать, что коэффициент а11 при x1 отличен от нуля, в противном случае мы можем поменять местами уравнения. Разделим все члены первого уравнения на а11 в результате получим систему вида
x1 + a12 x2 +... + a1n xn = b1
a21x1 + a22 x2 +... + a2n xn = b2
.......................... ()
an1 x1 + an2 x2 +... + ann xn = bn
Затем из каждого 2-го, 3-го,..., n-го уравнения вычитаем почленно 1-е уравнение, умноженное соответственно на a21, a31,..., an1. После этого наша система будет равносильна системе вида
x1 + a12 x2 +... + a1n xn = b1
a22 x2 +... + a2n xn = b2
.................... ()
an2 x2 +... + ann xn = bn.
В полученной системе поступаем таким же образом со всеми уравнениями, начиная со второго. Затем переходим к рассмотрению уравнений, начиная с третьего. Продолжая указанный процесс, мы получим в результате треугольную систему вида
x1 + w 12 x2 +... + w 1n xn = d1
x2 +... + w 2n xn = d2
................ ()
x n-1 + w nn xn = d n-1
xn = d n
К полученной системе применим процедуру последовательного нахождения неизвестных. Последнее уравнение системы дает значение x n. Подставив полученное значение в предпоследнее уравнение найдем значение неизвестной x n-1 и т. д. В результате найдем значения всех неизвестных x1,..., x n.
Пример.
x1 + 3x2 + x3 = 14
2x1 + 8x2 - x3 = 22
x1 + 6x2 + 2x3 = 27
Из 2-го и 3-го уравнения вычитаем почленно 1-е уравнение, умноженное соответственно на 2 и 1. После этих операций получим систему
x1 + 3x2 + x3 = 14
2x2 - 3x3 = - 6
3x2 + x3 = 13.
Мы исключили x1 из 2-го и 3-го уравнения. Для исключения неизвестной x3 из 3-го уравнения разделим все члены 2-го уравнения на 2
x1 + 3x2 + x3 = 14
x2 - 1.5x3 = -3
3x2 + x3 = 13.
Затем из 3-го уравнения вычитаем 2-е, умноженное на 3. В результате получим
x1 + 3x2 + x3 = 14
x2 - 1.5x3 = -3
5.5x3 = 22.
Разделив 3-е уравнение на 5.5, находим x3 = 4. Подставляя x3 во 2-е уравнение, получим x2 - 1.5´ 4 = -3 или x2 = 3. Подставляя найденные значения в 1-е уравнение, получим x1 + 3´3 + 4 = 14 или x1 = 1.
Другую реализацию метода исключения неизвестных можно назвать методом диагонализации. Данный метод отличается от метода Гаусса тем, что в нем каждое из неизвестных xk исключается из всех уравнений кроме одного. Таким образом он доводит решение системы до конца и не требует применения процедуры последовательного нахождения неизвестных. Часто решение оформляется в матричном или табличном виде.
Пример.
x1 + x2 - 2x3 = 4
3x1 + x2 + x3 = 9
2x1 + x2 - x3 = 6
Рассмотрим расширенную матрицу системы
.
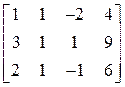Приведем матрицу системы к единичному виду. Тогда в последнем столбце получим решение системы. Вычитаем из 2-й и 3-й строки первую, умноженную соответственно на 3 и 2. После выполнения операций получим матрицу
.
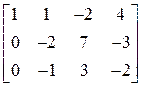Разделим 3-ю строку на -1 и переставим со 2-й строкой. Получим матрицу
.
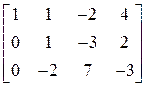Вычитаем из 1-й и 3-й строки вторую, умноженную соответственно на 1 и -2. Получим матрицу
.
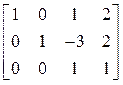В заключении, вычитаем из 1-й и 2-й строки третью, умноженную соответственно на 1 и -3. В результате получим
.
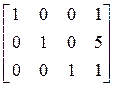Следовательно x1 = 1, x2 = 5, x3 = 1.
