Опр.1: pϵ Z \{0;±1} наз. простым, если оно делится только лишь на ±1 и ±p.
Опр.2: aϵ Z \{0;±1} наз.я составным, если оно им. хотя бы 1 делитель отл-й от ±1; ±a. Пр-ры: простые целые числа - ±2, ±3, ±5; составные - ±4, ±6, ±8, ±20.
Свойства простых чисел: 1°. pϵ P, aϵ N, p:a => p=a.2°. p1, p2ϵ P ^ p1 ≠ p2 => p1 не: p2Ùp2 не: p1. 3°. aϵ N \{1} имеет хотя бы один простой делитель.
4°. pϵ P, aϵ N => НОД(a,p)=1 Ú a:p. 5°. a·b:p, a,bϵ N, pϵ P => a:p Ú b:p.
6°. Наименьший простой делитель p составного числа a не превосходит Öa.
7°. Теорема Евклида: Мн. простых чисел есть ∞ мн.. Док-во: Предп.что P -конечное, P ={ p1, p2… pk}. Составим число n= p1·p2···pk+1, nÏ P, это число n≠1 => n - составное. Пусть n:p1Þ 1:p1 –противоречие
Решето Эратосфена:
Для нахожд-я всех прост. чисел не >зад-го числа n н. вып-ть след. шаги:
1. Выписать подряд все цел. числа от двух до n. 2. p=2 - 1му простому числу.
3. Вычеркнуть из списка все числа от 2p до n, делящиеся на p (то есть, числа 2p, 3p, 4p, …) 4. Найти 1е не вычеркнутое число >, чем p, и присвоить знач-ю переменной p это число. 5. Повторять шаги 3 и 4 до тех пор, пока p не станет >, чем n. 6. Все не вычеркнутые числа в списке — простые числа. n=30
Осн. Теор. арифметики (О фактореальности мн. N чисел): Всякое nϵN, n≠1, явл. либо простым, либо его м. предст. в виде произвед. Прост. сомножителей и притом однозначно с точн-ю до пор. их след-я или мн. P -факториально.
О: Предст-е nϵN в виде n= 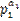 ·
· 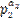 ···
···  наз. канонической записью числа n.
наз. канонической записью числа n.
Основная теорема арифметики утверждает, что любое натуральное число n можно представить в виде произведения простых чисел:
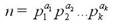
Такое разложение натурального числа называется каноническим. Из него следует, что если
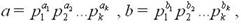
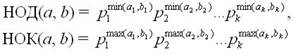
Рассмотрим числа a = 24 и b = 18. Разложим их на простые множители: 24 = 2^3·3, 18 = 2·3^2. Следовательно
НОД(24, 18) = 2^min(3,1) · 3^min(1,2) = 2^1 · 3^1 = 6,
НОК(24, 18) = 2^max(3,1) · 3^max(1,2) = 2^3 · 3^2 = 8 · 9 = 72
12. Сравнимость целых чисел по числовому модулю. Кольцо классов вычетов. Сравнения и их основные свойства. Полная и привидённая система вычетов.
О.1. Б. говорить, что а≡b(mod m) ↔ a-b дел. На m. О.2. Б.г., что a≡b(mod m) ↔ сущ. t принадл. Ζ, a=b+mt. О.3. Б.г., что a≡b(mod m) ↔ сущ. t1,t2 принад. Ζ, такие что a=mt1+r, b=mt2+r. 0≤r<m.
Например: 32 и −10 сравнимы по модулю 7, так как

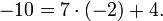
Свойства: 1)Отн.сравн-ти Ζ по фиксир-му мод. m явл. отн. эквив-ти зад-м на мн.Ζ.2) всякое целое число кратное модулю сравнимо с 0 по дан. модулю.
3) всяк. цел. число сравнимо со своим остатком от дел-я на модуль.
4) сравнения по 1му и тому же модулю м. +, вычитать- и переумножать.
5)обе части сравнения м. * на 1 и то же целое число. 6)обе части сравн-я и модуль м.*на 1 и то же нат. число. 7)обе части сравн. и модуль м.о / на их общ. множитель.8)обе части сравн-я м. делить на их общ. дел-ль если он взаимно прост с mod. Док-во: ak≡bk(mod m) и нод(k,m)=1, то a≡b(mod m); ak≡bk(mod m)→ak-bk дел. На m →k(a-b) дел.на m и нод(k,m)=1 →a-b дел.на m.
9)если 1 и то же сравн-е им. место по разл. модулям
a≡b(mod m1) и a≡b(mod m2) то a≡b(mod m), m = нок(m1,m2).
Док-во: a-b дел.на m1 и a-b дел.на m2 доказать, что a-b дел.на m, где m=нок(m1,m2). Если a-b дел.на m1, а m1 делиться и на m. Аналогично a-b дел.на m2 и m2 делиться и на m, то a-b дел.на m.
Опред.класса вычетов: т.к. отн-е сравнимости, по фиксир-му модулю m явл.отн-ем эквив-ти, то само как и всякое отн. эквив. порождает разбиение мн. на кот. оно задано(в дан.случае Ζ) на классы эквив. кот. наз. кл-ми вычетов по mod m [a]m:={bпринад. Ζ/ a≡b(mod m)} т.к. остатков от дел-я Ζ чисел на m будет только m, то и классов вычетов будет m: [0]m, ….,[m-1]m.
Теорема: множество классов вычетов яв.<Ζm,+,•> яв. коммут.кольцом с единицей.
Полная сист. вычетов: если с кажд. кл. вычетов по мод. m выбрать по 1му представителю, то получ-я сист. вычетов наз.полн. сист. вычетов по мод.m.
Пример: Пусть m = 5. Тогда:
0, 1, 2, 3, 4 - наименьшие неотрицательные вычеты;
-2, -1, 0, 1, 2 - абсолютно наименьшие вычеты.
Обе приведенные совокупности чисел образуют полные системы вычетов по модулю 5.
Прbвиденная сист. вычетов:
Приведенной системой вычетов по модулю m называется совокупность всех вычетов из полной системы, взаимно простых с модулем m.
Пусть m = 42. Тогда приведенная система вычетов суть:
1, 5, 11, 13, 17, 19, 23, 25, 29, 31, 37, 41.






