Означення. Результатом многочленів 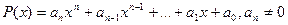 та
та 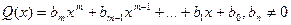 називається число
називається число  , де
, де 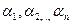 - корені многочлена
- корені многочлена  .
.
Властивість1.  де
де


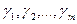 - корені многочлена
- корені многочлена  .
.
Властивість 2. 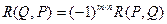
Властивість 3.




 …
… 
 …
…
.  …
… 
 …
…
...
… 
 …
… 


 …
… 
 …
…
.  …
… 
 …
…
...
… 
 …
… 

Ця форма результата називається формою Сільвестра.
Теорема 1. Якщо многочлени  і
і  мають спільний корінь, то
мають спільний корінь, то  .
.
Теорема 2. Якщо  , то або многочлени
, то або многочлени  та
та  мають спільний корінь або обидва їх старші коефіціенти дорівнюють нулю.
мають спільний корінь або обидва їх старші коефіціенти дорівнюють нулю.
Розглянемо систему алгебраїчних рівнянь:
 (1)
(1)

Розглядаючи  як параметр, побудуємо
як параметр, побудуємо 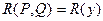
 є алгебраїчним многочленом відносно
є алгебраїчним многочленом відносно  степеня
степеня  , який не перевищує добутку степенів многочленів
, який не перевищує добутку степенів многочленів  ,
,  (відносно обох змінних).
(відносно обох змінних).
Многочлен  має в полі комплексних чисел
має в полі комплексних чисел  коренів
коренів  . Якщо результат дорівнює нулю, то на основі теореми 2 многочлени
. Якщо результат дорівнює нулю, то на основі теореми 2 многочлени
 (2)
(2)

Або мають спільний корінь, або їх старші коефіціенти  ,
,  дорівнюють нулю.
дорівнюють нулю.
1. Якщо хоча б один з коефіціентів  ,
,  відмінний від нуля, то
відмінний від нуля, то  ,
,  мають спільний корінь
мають спільний корінь 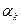 . Пара чисел
. Пара чисел  є одним з розв’язків системи (2). Для даного
є одним з розв’язків системи (2). Для даного  може бути декілька спільних коренів
може бути декілька спільних коренів  ,
,  , наприклад,
, наприклад,  . Тоді пари чисел
. Тоді пари чисел 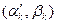 ,
,  є розв’язками системи (2).
є розв’язками системи (2).
2. Якщо 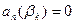 та
та 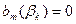 то
то  та
та  можуть і немати спільних коренів. Тоді
можуть і немати спільних коренів. Тоді  ми відкидаємо. Якщо ж
ми відкидаємо. Якщо ж  ,
,  мають спільний корінь
мають спільний корінь 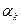 , то
, то  -розв’язок системи.
-розв’язок системи.
Щоб знайти всі розв’язки системи рівнянь (1) потрібно розглянути алгебраїчно всі корені результата  .
.
Таким чином, щоб розв’язати систему алгебраїчних рівнянь (1) потрібно:
1) Побудувати результат  та знайти всі його корені;
та знайти всі його корені;
2) Знайдений корінь  підставити в многочлени
підставити в многочлени  ,
,  .
.
3) Знайти найбільший спільний дільник 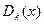 многочленів
многочленів  ,
,  .
.
4) Розв’язати рівняння  . Корені цього рівняння
. Корені цього рівняння  є спільними коренями многочленів
є спільними коренями многочленів  та
та  .
.
5) Скласти систему пар чисел  .
.
Приклад. Розв’язати систему рів7нянь:

Обчислимо результат  :
:







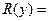




 .
.








Коренями  будуть
будуть 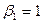 ;
;  ;
;  .
.
1). 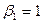 ,
, 

Спільного кореня немає. В цьому випадку система немає розв”язку.
2).  ,
, 

Спільним коренем буде 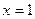 . Отже,
. Отже,  є розв’язком системи.
є розв’язком системи.
3)  ,
, 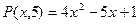
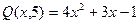
Спільний корінь  . Отже,
. Отже,  - є розв’язком системи рівнянь.
- є розв’язком системи рівнянь.
Відповідь:  ,
,  .
.
Розв’язати систему рівнянь:
1. 
2. 
3. 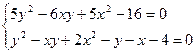
4. 
5. 
6. 
7. 
8. 
9. 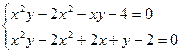
10. 
11. 
12. 
13. 
14. 
15. 
16. 
17. 
18. 
19. 
20. 
21. 
При якому  мають спільні корені многочлени:
мають спільні корені многочлени:
22. 

23. 
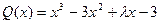
24. 

25. 

Обчислити результати многочленів:
26. 

27. 
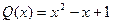
28. 
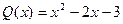
29. 
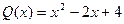
30. 

Література
1. Чарін В.С. Лінійна алгебра. К.:Техніка,2004,-413с.
2. Саушкін О.Ф. Рівняння вищих степенів, методи їх розв’язання. - К.:КНЕУ,1999.-99с.
3. Завало С.Т. та інші. Алгебра і теорія чисел. - К.:Вища школа.1976-384с.
4.Марач В.С., Крайчук О.В. Індивідуальні завдання з алгебри і теорії чисел. IV семестр. - Рівне,1990.
5. Фадєєв Д.К.,Сочінський І.С. Збірник задач з вищої алгебри. - К.:Вища школа,1971. - 316с.
6. Лельчук М.П. Збірник задач з алгебри і теорії чисел. - К.:Вища школа,1987.






