В этом случае  (при
(при 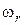 >
> 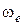 ). Мгновенная ось вращения и мгновенный центр скоростей находятся за вектором большей угловой скорости на расстояниях таких, что
). Мгновенная ось вращения и мгновенный центр скоростей находятся за вектором большей угловой скорости на расстояниях таких, что 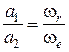 (опять по аналогии определения равно- действующей параллельных сил).
(опять по аналогии определения равно- действующей параллельных сил).
 3. Оси вращения параллельны, направления вращений противоположны и угловые скорости равны.
3. Оси вращения параллельны, направления вращений противоположны и угловые скорости равны.
Угловая скорость абсолютного движения  и, следовательно, тело совершает поступательное движение. Этот случай называется парой вращений, по аналогии с парой сил.
и, следовательно, тело совершает поступательное движение. Этот случай называется парой вращений, по аналогии с парой сил.
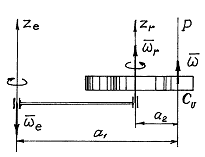
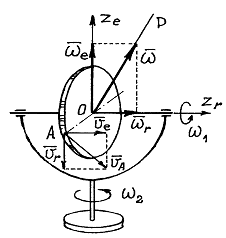
Пример 1: Диск радиусом R вращается вокруг горизонтальной оси с угловой скоростью  , а эта ось вместе с рамкой вращается вокруг вертикальной неподвижной оси с угловой скоростью
, а эта ось вместе с рамкой вращается вокруг вертикальной неподвижной оси с угловой скоростью  (рис.11.4).
(рис.11.4).
Горизонтальная ось – это ось относительного вращения  ; вертикальная ось – ось переносного вращения
; вертикальная ось – ось переносного вращения 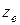 . Соответственно угловые скорости
. Соответственно угловые скорости 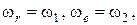 векторы их направлены по осям
векторы их направлены по осям 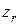 и
и 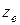 .
.
Абсолютная угловая скорость 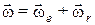 , а величина ее, так как
, а величина ее, так как  ,
,
 .
. 
Скорость точки А, например, можно найти или как сумму переносной и относительной скоростей: 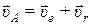 , где
, где 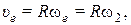
 и
и 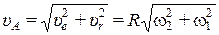 ,
,
или как при абсолютном движении, при вращении вокруг мгновенной оси Р, 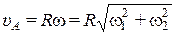
Вектор скорости 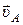 будет расположен в плоскости перпендикулярной вектору
будет расположен в плоскости перпендикулярной вектору 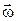 и оси Р.
и оси Р.
Пример 2: Водило ОА с укрепленными на нем двумя колесами 2 и 3 вращается вокруг оси О с угловой скоростью 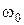 . Колесо 2 при этом будет обкатываться по неподвижному колесу 1 и заставит вращаться колесо 3. Найдем угловую скорость
. Колесо 2 при этом будет обкатываться по неподвижному колесу 1 и заставит вращаться колесо 3. Найдем угловую скорость  , этого колеса. Радиусы колес
, этого колеса. Радиусы колес 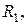
 .
.
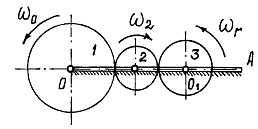 Колесо 3 участвует в двух движениях. Вращаться вместе с води- лом вокруг оси О и относительно оси
Колесо 3 участвует в двух движениях. Вращаться вместе с води- лом вокруг оси О и относительно оси  . Ось О будет переносной осью, ось
. Ось О будет переносной осью, ось  – относительной. Переносная угловая скорость колеса 3 – это угловая скорость водила
– относительной. Переносная угловая скорость колеса 3 – это угловая скорость водила  , направленная по часовой стрелке, как
, направленная по часовой стрелке, как 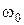 .
.
 Чтобы определить угловую скорость относительного движения, наблюдателю нужно находиться на водиле. Он увидит водило неподвижным, колесо 1 вращающимся против часовой стрелки со скоростью
Чтобы определить угловую скорость относительного движения, наблюдателю нужно находиться на водиле. Он увидит водило неподвижным, колесо 1 вращающимся против часовой стрелки со скоростью 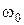 , а колесо 3 – вращающимся с относительной угловой скоростью
, а колесо 3 – вращающимся с относительной угловой скоростью 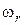 , против часовой стрелки.
, против часовой стрелки.
Так как  , то
, то 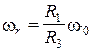 . Оси вращения параллельны, направления вращений противоположны. Поэтому
. Оси вращения параллельны, направления вращений противоположны. Поэтому 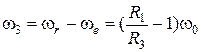 и направлена так же, как
и направлена так же, как 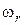 , против часовой стрелки. В частности, если
, против часовой стрелки. В частности, если 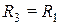 , то
, то 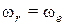 и
и 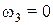 . Колесо 3 будет двигаться поступательно.
. Колесо 3 будет двигаться поступательно.
Сферическое движение
(Вращение тела вокруг неподвижной точки)
Наглядным примером такого движения является волчок, закономерности движения которого лежат в основе гироскопических приборов.
1) Углы Эйлера. Уравнения вращения тела с одной неподвижной точкой.
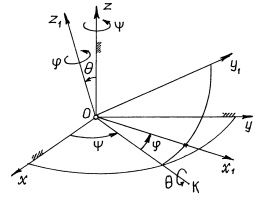 Положение тела определяется тремя углами. Самыми распространёнными являются углы Эйлера:
Положение тела определяется тремя углами. Самыми распространёнными являются углы Эйлера: 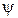 (пси),
(пси), 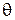 (тета),
(тета), 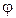 (фи).
(фи).
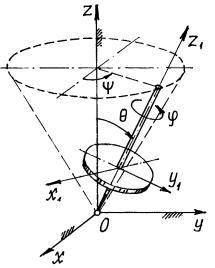
Первая система декартовых осей – неподвижные оси  . Начало которых берётся в неподвижной точке
. Начало которых берётся в неподвижной точке 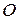 тела (рис. 1). Вторая система - оси
тела (рис. 1). Вторая система - оси 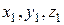 , связывается с телом. Поэтому положение тела будет определятся как положение этих осей относительно неподвижных.
, связывается с телом. Поэтому положение тела будет определятся как положение этих осей относительно неподвижных.
Линия пересечения неподвижной плоскости  и подвижной
и подвижной 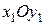 , прямая
, прямая 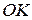 , называется линией узлов. Угол
, называется линией узлов. Угол 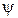 называется углом прецессии, угол
называется углом прецессии, угол 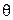 – углом нутации, угол
– углом нутации, угол 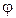 – углом собственного вращения. Эти названия углов пришли из теории гироскопов.
– углом собственного вращения. Эти названия углов пришли из теории гироскопов.
 При движении тела углы Эйлера изменяются по определённым законам:
При движении тела углы Эйлера изменяются по определённым законам: 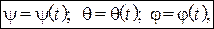 которые называются уравнениями вращения.
которые называются уравнениями вращения.
На примере вращающегося волчка можно лучше разобраться в этих углах Эйлера (рис. 2). Ось волчка 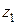 описывает конус вокруг неподвижной оси
описывает конус вокруг неподвижной оси 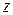 . Это вращение определяется углом
. Это вращение определяется углом 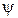 (говорят: волчок совершает прецессию). Отклонение оси волчка от вертикали – угол нутации
(говорят: волчок совершает прецессию). Отклонение оси волчка от вертикали – угол нутации  . А вращение волчка вокруг своей оси
. А вращение волчка вокруг своей оси  , определяемое углом
, определяемое углом 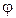 – собственное вращение.
– собственное вращение.
2) Теорема Даламбера – Эйлера. Мгновенная ось вращения.
Тело с одной неподвижной точкой можно переместить из одного положения в другое поворотом вокруг некоторой оси, проходящей через неподвижную точку  . Мгновенная ось вращения – геометрическое место точек, скорости которых равны нулю в данный момент времени. Ось
. Мгновенная ось вращения – геометрическое место точек, скорости которых равны нулю в данный момент времени. Ось 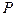 называют мгновенной осью вращения, а угловую скорость
называют мгновенной осью вращения, а угловую скорость 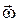 – мгновенной угловой скоростью, вектор которой направлен по оси.
– мгновенной угловой скоростью, вектор которой направлен по оси.
3) Скорость точек тела.
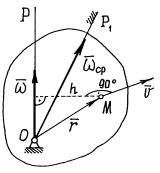 Определение скоростей точек тела значительно упрощается, если известна мгновенная ось вращения
Определение скоростей точек тела значительно упрощается, если известна мгновенная ось вращения 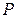 . Иногда её можно найти, если удастся обнаружить у тела хотя бы ещё одну точку, кроме
. Иногда её можно найти, если удастся обнаружить у тела хотя бы ещё одну точку, кроме  , скорость которой в данный момент равна нулю, и провести ось
, скорость которой в данный момент равна нулю, и провести ось 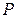 из неподвижной точки O через эту точку.
из неподвижной точки O через эту точку.
Скорость точки можно определить как скорость её при вращении тела вокруг мгновенной оси 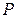 . Величина скорости
. Величина скорости 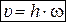 .
.
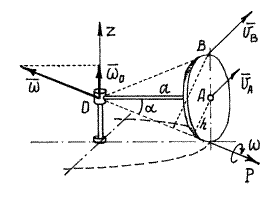
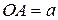 , вращаясь вокруг вертикальной оси
, вращаясь вокруг вертикальной оси 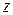 с угловой скоростью
с угловой скоростью 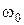 ,заставляет диск радиуса
,заставляет диск радиуса 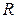 кататься по горизонтальной плоскости.
кататься по горизонтальной плоскости.
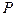 - мгновенная ось вращения. И вектор мгновенной угловой скорости
- мгновенная ось вращения. И вектор мгновенной угловой скорости 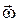 будет направлен по этой оси.
будет направлен по этой оси.
Точка 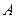 вместе с водилом
вместе с водилом 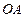 вращается вокруг оси
вращается вокруг оси 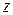 . Поэтому её скорость
. Поэтому её скорость  . Эта скорость определяет направление вращения диска вокруг оси
. Эта скорость определяет направление вращения диска вокруг оси 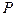 и направление вектора
и направление вектора 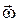 .Величина угловой скорости
.Величина угловой скорости 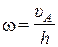 (h – расстояние от
(h – расстояние от 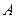 до оси
до оси 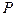 ). Теперь можно найти скорость любой точки диска, рассматривая его движение как вращение вокруг оси
). Теперь можно найти скорость любой точки диска, рассматривая его движение как вращение вокруг оси 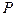 . Так, например, скорость точки
. Так, например, скорость точки 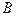
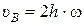 . Так как
. Так как  и
и 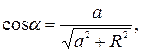
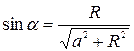 , то
, то 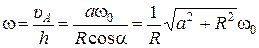 и
и 
4) Ускорение точек тела.
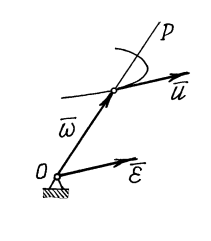 Сначала определим угловое ускорение тела
Сначала определим угловое ускорение тела 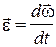 . При движении тела вектор угловой скорости
. При движении тела вектор угловой скорости 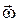 изменяется и по величине, и по направлению. Точка расположенная на его конце будет двигаться по некоторой траектории со скоростью
изменяется и по величине, и по направлению. Точка расположенная на его конце будет двигаться по некоторой траектории со скоростью  (рис. 5). Если рассматривать вектор
(рис. 5). Если рассматривать вектор 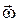 как радиус-вектор этой точки, то
как радиус-вектор этой точки, то 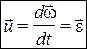
Угловое ускорение тела можно определить как скорость точки, расположен- ной на конце вектора угловой скорости:
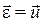 .
.
Этот результат называется теоремой Резаля.
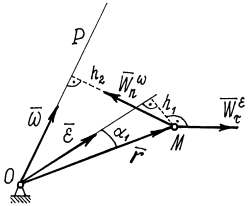
Ускорение какой-либо точки  тела
тела
 , есть сумма двух векторов.
, есть сумма двух векторов.
Первый вектор 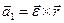 . Модуль его
. Модуль его  , где h1 – расстояние от точки
, где h1 – расстояние от точки 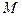 до вектора
до вектора  .Направлен он перпендикулярно
.Направлен он перпендикулярно  и
и 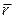 . Это касательное ускорение, предполагая, что тело вращается вокруг оси, совпадающей с вектором
. Это касательное ускорение, предполагая, что тело вращается вокруг оси, совпадающей с вектором  . И обозначается этот вектор ускорения так
. И обозначается этот вектор ускорения так 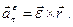
Второй вектор  Модуль его
Модуль его  , но
, но  , т.к. векторы
, т.к. векторы 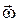 и
и  перпендикулярны друг другу. Значит
перпендикулярны друг другу. Значит  , где h2 – расстояние от точки М до мгновенной оси
, где h2 – расстояние от точки М до мгновенной оси 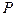 , до вектора
, до вектора 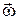 .
.
Направлен вектор 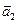 перпендикулярно
перпендикулярно 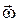 и
и  , т.е. так же как вектор нормального ускорения при вращении вокруг оси
, т.е. так же как вектор нормального ускорения при вращении вокруг оси 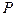 , или вектора
, или вектора 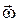 . Поэтому этот вектор ускорения и обозначают, соответственно, так:
. Поэтому этот вектор ускорения и обозначают, соответственно, так:
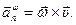
Итак, ускорение точек тела, вращающегося вокруг неподвижной точки, определяется как сумма двух ускорений:

Этот результат называется теоремой Ривальса.






