Рекурсивные методы построения алгоритмов
Вариант 1. Описать рекурсивную функцию DigitSum(K) целого типа, которая находит сумму цифр целого числа K без использования оператора цикла.
Вариант 2. Вычислить сумму: 
, используюя функцию вычисления факториала числа 
Вариант 3. Описать рекурсивную функцию SqrtK(X, K, N) вещественного типа, находящую приближенное значение корня k-й степени из числа X по формуле:
где Yn обозначает SqrtK(X, K, N) при фиксированных X и K. Параметры функции: X > 0 — вещественное число, K > 1 и N > 0 — целыt/
Вариант 4. Описать рекурсивную функцию NOD(A, B) целого типа, находящую наибольший общий делитель (НОД) двух целых положительных чисел A и B, используя алгоритм Евклида: NOD(A, B) = NOD(B mod A,B), если A <> 0; НОД(0, B) = B.
Вариант 5. Описать рекурсивную функцию 
целого типа, вычисляющую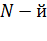 
элемент последовательности чисел Фибоначчи (
— целое число): Считать, что номер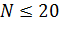 
. Для уменьшения количества рекурсивных вызовов по сравнению с функцией создать вспомогательный массив для хранения уже вычисленных чисел Фибоначчи и обращаться к нему при выполнении функции Fib.
Вариант 6. Описать рекурсивную функцию Fact2(N) вещественного типа, вычисляющую значение двойного факториала N!! = N·(N-2)·(N-4)·...., где N > 0 — параметр целого типа; последний сомножитель в произведении равен 2, если N — четное число, и 1, если N — нечетное.
Вариант 7. Напишите рекурсивную функцию SumTo(n), которая для данного n вычисляет сумму чисел от 1 до n.
Методы сортировки данных
Реализуйте все простые сортировки линейного массива, используя процедуры, и оцените трудоемкость каждого алгоритма.
Вариант 1. Дан массив целых чисел осуществить сортировку четных элементов массива.
Вариант 2. Дан массив целых чисел осуществить сортировку элементов массива записанных на нечетных местах.
Вариант 3. Дан массив целых чисел осуществить сортировку отрицательных элементов массива.
Вариант 4. Дан массив целых чисел осуществить сортировку положительных элементов массива. Вариант 5. В упорядоченный по возрастанию значений элементов массив М, состоящий из целых чисел, необходимо вставить число, не нарушив упорядоченности исходного массива.
Вариант 6. Задан массив М, состоящий из N целочисленных элементов. Упорядочить элементы таким образом, чтобы вначале располагались все нечетные аргументы, а после них все четные.
Вариант 7. Задан массив М, состоящий из N целочисленных элементов. Упорядочить элементы таким образом, чтобы вначале располагались все четные аргументы, а после них все нечетные.
Вариант8. Задан массив М, состоящий из N целочисленных элементов. Упорядочить элементы таким образом, чтобы вначале располагались все положительные аргументы, а после них все отрицательные.
Вариант 9. Задан массив М, состоящий из N целочисленных элементов. Упорядочить элементы таким образом, чтобы вначале располагались все отрицательные аргументы, а после них все положительные.
Вариант 10. Массив М, состоящий из 30 элементов, переформировать так, чтобы вначале стояли все положительные элементы в порядке убывания их значений, а затем все отрицательные элементы в порядке возрастания их значений.
Метод перебора в задачах поиска
Вариант 1. Дана вещественная матрица А(N,M). Составить программу замены всех положительных элементов матрицы на элемент, имеющий минимальное значение.
Вариант 2. Дана вещественная матрица А(N,M). Составить программу нахождения максимального отрицательного элемента матрицы и нахождения его местоположения.
Вариант 3. Дана вещественная матрица А(N,M). Составить программу замены всех отрицательных элементов матрицы на элемент, имеющий максимальное значение.
Вариант 4. Составить программу замены всех отрицательных элементов матрицы А(N,N) на элемент этой матрицы, имеющий минимальное значение. Скорректированную матрицу напечатать.
Вариант 5. Дана вещественная матрица А(N,M).Составить программу нахождения минимального положительного элемента матрицы и нахождения его местоположения.
Вариант 6. Составить программу замены всех отрицательных элементов матрицы А(6,6) на 0, если сумма минимального и максимального элементов этой матрицы окажется меньше Р.
ЗАКЛЮЧЕНИЕ
В результате проделанной работы создано учебное пособие по дисциплине «Теория алгоритмов» для студентов Политехнического колледжа НовГУ обучающихся по специальности 230115 «Программирование в компьютерных системах».
Учебное пособие разработано в соответствии с рабочей программой дисциплины «Теория алгоритмов» и отвечает всем требованиям к результатам освоения студентами данной дисциплины.
Учебное пособие состоит из двух разделов. В ходе работы был проведен анализ научных и литературных источников, на основе которых в первом разделе раскрыты понятия алгоритма и вспомогательного алгоритма, основные алгоритмические структуры, рассмотрена формализация понятия «алгоритм» на примерах виртуальных машин Поста и Тьюринга. В результате работы над вторым разделом пособия изучены и систематизированы основные методы сортировки данных и поиска заданных элементов в массивах, а так же рассмотрено понятие сложности алгоритма. В каждом разделе пособия рассмотрены примеры решения типовых задач, представлены блох-схемы алгоритмов.
В Приложении 1, прилагаемом к учебному пособию, представлены программы на языке Pascal для разобранных примеров.
В конце каждого раздела предложены задания для самостоятельной работы студентов.
В ходе дальнейшей работы над пособием целесообразно будет разработать контрольно-диагностический материал в виде тестов по курсу «Теория алгоритмов», а так же создать программный продукт для автоматизации подсчетов результатов тестирования.
Разработанное учебное пособие может быть рекомендовано студентам средних специальных учебных заведений для самостоятельного изучения дисциплины "Теория алгоритмов».
СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ
1. Игошин В.И.Теория алгоритмов: Учебное пособие. – М.:ИНФРА-М, 2013.- 318 с.
2. Канцедал С.А. Алгоритмизация и программирование: учебное пособие. – М.: ИД «ФОРУМ»: ИНФРА-М, 2014. – 352 с.
3. Колдаев В.Д., Павлова Е.Ю. Сборник задач и упражнений по информатике. - М.: ИД «ФОРУМ»: ИНФРА-М, 2010. – 256 с.
4. Марченко А.И., Марченко Л.А. Программирование в среде Turbo Pascal 7.0. – К.: ВЕК+, 1999. – 464 с.
5. Немцова Т.И., Голова С.Ю., Абрамова И.В. Программирование на языке высокого уровня. Программирование на языке Object Pascal. - М.: ИД «ФОРУМ»: ИНФРА-М, 2012. – 496 с.
6. Окулов С.М. Основы программирования. – М.: БИНОМ. Лаборатория знаний, 2010. – 440 с.
7. Попов В. Б. Turbo Pascal для школьников. – М.: Финансы и статистика, 2000. – 528 с.
8. Цымбалюк Л.Н. Основы алгоритмизации и программирования: Практикум «Работа в программе Borland Pascal». – П.-К.: Камчатский кооперативный техникум, 2009. – 111 с.
9. Методические материалы и программное обеспечение: [Электронный ресурс], http://kpolyakov.narod.ru/, (Дата обращения 24.02 2015).
10. Кнут Д. Искусство программирования. Т.3. [Электронный документ], www.eknigi.org. (Дата обращения 15.04.2015).
11. Рублев В.С. Основы теории алгоритмов: учебное пособие. – Ярославль, 2005. [Электронный документ], www.ivt.corp7.uniyar.ac.ru. (Дата обращения 24.03.2015)
12. Фалина И.Н., Радченко Е.Л. «Изучение машины Поста в школьном курсе информатики». [Электронный документ], www.inf.1september.ru. (Дата обращения 30.03.2015)
13. Рабочая программа дисциплины «Теория алгоритмов».
