ГЛОССАРИЙ
К УЧЕБНОЙ ОБЩЕУНИВЕРСИТЕТСКОЙ ДИСЦИПЛИНе
ФИЗИКА
ПОНЯТИЯ, определения, формулы, уравнения
РАЗДЕЛ 1.Физические основы механики
| РАЗДЕЛ 1.Физические основы механики | ||
| Понятие | Определение, формула, уравнение | См. в Конспектах лекций (семестр 2): |
| А.т.т. | См. Абсолютно твердое тело | |
| Абсолютно твердое тело | Абсолютно твердое тело имеет одинаковые с реальным телом размеры и форму, но отличается абсолютной жесткостью. Все размеры тела неизменны. Пренебрегаем деформациями, не учитываем колебательных движений в теле. | 1.1 1.2 |
| Анизотропность времени | См. Время - анизотропность | |
| Аксиальные векторы | См. Векторы аксиальные | |
| Вектор линейного перемещения | См. Перемещение линейное - вектор | |
| Вектор угла поворота | См. Угол поворота - вектор | |
| Вектор углового перемещения | См. Угловое перемещение - вектор | |
| Векторы полярные | Направление линейных (полярных) векторов – естественное: оно задается направлением и характером движения. | 1.2 1.3 |
| Векторы аксиальные | Направление осевых (аксиальных) векторов – условное: оно определяется по правилу правого винта, ввинчивающегося вдоль оси вращения. Их модуль равен значению соответствующей физической величины. | 1.2 1.4 |
| Взаимодействия фундаментальные | См.Фундаментальные силы. | |
| Время | Совокупность отношений, выражающих последовательность и длительность событий. | 1.1 3.1 |
| Время - анизотропность | Для времени характерно выделенное направление – "стрела времени": все события развиваются от прошлого через настоящее к будущему | 3.1 |
| Время - одномерность | Момент события описывается одним числом | 3.1 |
| Время - однородность | Одно и то же событие развивается одинаково в разные моменты времени. | 3.1 |
| Геометрия Евклида | Описывает пустое, безграничное, изотропное пространство, имеющее три измерения. Бесконечность пространства характеризуется несколькими постулатами, например, «от всякой точки до всякой точки можно провести прямую линию», «ограниченную прямую можно непрерывно продолжать по прямой», «из всякого центра и всяким раствором может быть описан круг», «через точку вне прямой на плоскости проходит лишь одна прямая, не пересекающая эту прямую». Свойства евклидова пространства и его геометрию, отличную от неевклидовых геометрий (Лобачевского, Римана и т.п.) определяются учением о параллельных и знаменитым пятым постулатом – «если прямая, падающая на две прямые, образует внутренние и по одну сторону углы меньшие 1800, то продолженные неограниченно эти две прямые обязательно пересекаются с той стороны от третьей прямой, по которой расположены углы, составляющие вместе менее 1800». | 1.3 |
| Градиент скалярной величины | Вектор, направленный в сторону быстрейшего увеличения этого же скаляра. | 1.7 |
| Градиент потенциальной энергии | Вектор, направленный в сторону быстрейшего увеличения потенциальной энергии:
grad U=  =- =- 
| 1.7 |
| Движение вращательное общее | В общем случае твердое тело может находиться во вращении относительно трех взаимно перпендикулярных осей, пересекающихся в одной точке. Это вращение относительно неподвижной точки, при котором все точки т.т. движутся по поверхности концентрических сфер с центрами в фиксированной точке. | 1.2 1.4 |
| Движение вращательное простое (или осевое) | При простом вращательном движении все точки твердого тела описывают окружности в параллельных плоскостях; центры этих окружностей лежат на одной прямой, называемой осью вращения Ось вращения фиксирована. | 1.2 1.4 |
| Движение вращательное простое - уравнения кинематические в координатной форме |

| 1.2 1.4 |
| Движение вращательное простое равнопеременное - уравнения кинематические в координатной форме |

| 1.2 1.4 |
| Движение вращательное простое равномерное - уравнения кинематические в координатной форме |

| 1.2 1.4 |
| Движение вращательное простое - уравнения кинематические в векторной форме |

| 1.2 1.4 |
| Движение вращательное простое равнопеременное - уравнения кинематические в векторной форме | 
| 1.2 1.4 |
| Движение вращательное простое равномерное - уравнения кинематические в векторной форме |
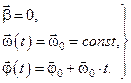
| 1.2 1.4 |
| Движение поступательное - уравнения кинематические в векторной форме |

 При ускоренном движении угол между
При ускоренном движении угол между 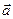 и и  находится в пределах 0 … 90°.
При замедленном движении угол между находится в пределах 0 … 90°.
При замедленном движении угол между 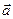 и и  находится в пределах 90°… 180°. находится в пределах 90°… 180°.
| 1.2 1.3 |
| Движение поступательное равнопеременное – уравнения кинематические в векторной форме | 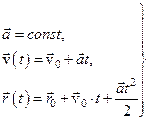
| 1.2 1.3 |
| Движение поступательное равномерное - уравнения кинематические в векторной форме | 
| 1.2 1.3 |
| Движение поступательное - уравнения кинематические в траекторной форме |
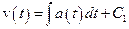

| 1.2 1.3 |
| Движение поступательное равнопеременное – уравнения кинематические в траекторной форме | 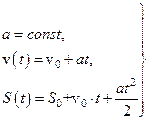
| 1.2 1.3 |
| Движение поступательное равномерное - уравнения кинематические в траекторной форме | 
| 1.2 1.3 |
| Дефект массы | 
| 1.7 3.1 |
| Естествознание | Естествознание есть совокупность наук об основных свойствах материи, о видах материи, которые входят в состав любых сложных материальных систем; о взаимодействиях этих видов материи и их движении. | Введение в курс общей физики |
| Закон Гука | 
| 1.3 |
| Закон всемирного тяготения | 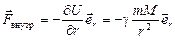
| 1.2 |
| Закон инерции | См. Закон Ньютона первый | |
| закон основной -динамики материальной точки (в линейных параметрах) | См. Закон Ньютона второй | |
| Закон основной – динамики материальной точки в орбитальном движении (в угловых параметрах) |  ,
или ,
или
 . .
| 1.4 |
| Закон Ньютона первый | В случае  =0 м.т. сохраняет состояние покоя или равномерного прямолинейного движения. В первом законе Ньютона содержится идея существования инерциальных систем отсчета.
Обобщением закона инерции – I закона Ньютона - является закон сохранения импульса замкнутой системы для свободно движущейся материальной точки (i = 1): =0 м.т. сохраняет состояние покоя или равномерного прямолинейного движения. В первом законе Ньютона содержится идея существования инерциальных систем отсчета.
Обобщением закона инерции – I закона Ньютона - является закон сохранения импульса замкнутой системы для свободно движущейся материальной точки (i = 1):
 . .
| 1.3 |
| Закон Ньютона второй |  ,
или ,
или
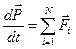
| 1.3 |
| Закон Ньютона третий | При взаимодействии двух м.т. векторная сумма сил будет равна нулю:
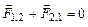 ,
то есть силы, с которыми действуют друг на друга взаимодействующие тела, равны по величине и противоположны по направлению (действие равно противодействию). ,
то есть силы, с которыми действуют друг на друга взаимодействующие тела, равны по величине и противоположны по направлению (действие равно противодействию).
| 1.3 |
| Закон основной – динамики твердого тела в простом вращательном движении | 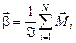 или
или
 ,
Под действием момента силы изменяется осевой момент импульса и возникает угловое ускорение: ,
Под действием момента силы изменяется осевой момент импульса и возникает угловое ускорение:
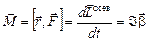 . .
| 1.4 |
| Закон основной - динамики материальной точки в НИСО | 
| 1.3 |
| Закон релятивистский -динамики материальной точки | 
| 3.1 |
| Закон распространения света | скорость света в вакууме не зависит от скорости движения приемника и источника, а также от направления распространения света в свободном пространстве. | 3.1 |
| Закон сложения скоростей (классический) | 
| 1.3 3.1 |
| Закон сложения скоростей (релятивистский) | 
| 3.1 |
| Закон сохранения импульса | Является следствием однородности пространства:
полный (суммарный ) импульс замкнутой системы тел тел сохраняется при любых процессах, происходящих в этой системе.
 или или
 , ,
| 1.5 |
| Закон сохранения момента импульса | Является следствием изотропности пространства:
в замкнутой системе суммарный момент импульса сохраняется:
 ,
или ,
или
 . .
| 1.5 |
| Закон сохранения энергии | Является следствием однородности времени.
При взаимодействии тел без диссипации (рассеяния) энергии
полная механическая энергия замкнутой и изолированной от любых внешних воздействий системы тел, в которой действуют лишь консервативные силы, есть величина постоянная:
 и E 'мех = Е" мех.
При взаимодействии тел при наличии диссипации энергии
в замкнутой и изолированной системе остается постоянной сумма всех видов энергии (включая и немеханические): и E 'мех = Е" мех.
При взаимодействии тел при наличии диссипации энергии
в замкнутой и изолированной системе остается постоянной сумма всех видов энергии (включая и немеханические):

| 1.7 |
| Законы сохранения (законы движения замкнутых систем) | В любой замкнутой механической системе тел полный импульс Р, полный момент импульса L и полная энергия Е с о х р а н я ю т с я, т.е. остаются неизменными с течением времени при любых процессах, происходящих в системе. законы сохранения импульса, момента импульса и энергии - это законы движения замкнутых систем. | 1.7 |
| Изотропность пространства | См. Пространство - изотропность | |
| Импульс | Векторная физическая величина, количественно характеризующая запас поступательного движения:
 
| 1.3 |
| Импульс - модуль вектора | 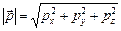
| 1.3 1.5 |
| Импульс полный системы материальных точек | Есть импульс материальной точки массой, равной полной массе системы м.т. или твердого тела, которая расположена в центре масс и движется со скоростью центра масс:

| 1.3 1.5 |
| Кинематика | Изучает движение тел (ускорение, скорость,кинематические уравнения движенияи форму траектории), не интересуясь причинами, обуславливающими это движение | 1.2 |
| М.т. | См. Материальная точка | |
| Материальная точка | Это тело, размерами и формой которого можно пренебречь в условиях данной задачи. М.т. заменяет движение реального тела движением одной любой из его точек. Движение других точек тела не рассматривается. Эта модель применима при пренебрежимо малых размерах тела по сравнению с расстояниями до других тел иди расстояниями, пройденными телом. Рассматривая реальное тело как м.т., пренебрегают перемещением отдельных его частей, вращательным движением тела и т.д. | 1.1 1.2 |
| Масса | Скалярная физическая величина, количественно характеризующая инертные и гравитационные свойства тела. | 1.3 |
| Масса гравитационная | Характеризует способность тела создавать гравитационное поле и взаимодействовать с внешними гравитационными полями | 1.3 |
| Масса инертная | Характеризует способность тела сопротивляться изменению своего состояния (покоя или движения) | 1.3 |
| Масса покоя | Наименьшая возможная масса тела, измеренная в той системе отсчета, в которой данное тело покоится. | 1.3 3.1 |
| Масса релятивистская | Масса, зависящая от скорости m = γ m 0 | 3.1 |
| Механика | Раздел физики, в котором изучается механическое движение материальных тел и проходящие при этом взаимодействия между ними | 1.1 |
| Механика классическая | По современным представлениям - это механика Галилея - Ньютона и механика Эйнштейна. | 1.1 |
| Механика Галилея – Ньютона | описывает механическое движение, происходящее со скоростью, значительно меньшей скорости света (С = 3,108 м/с). Есть предельный случай релятивистской механики при V << С и предельный случай квантово- волновой механики при   0. 0.
| 1.1 |
| Механика Эйнштейна (релятивистская) | Описывает движение со скоростями v, близкими к c. Базируется на специальной теории относительности А. Эйнштейна. | 3.1 |
| Механика квантово-волновая | Изучает движение частиц в микромире. | |
| Механическое движение | См. Движение механическое | |
| Момент импульса | Физическая векторная величина, характеризующая количество и направленность запасенного твердым телом простого вращательного движения (или запас поступательного движения материальной точки в угловых параметрах). | 1.4 |
| Момент импульса осевой | Параллелен вектору угловой скорости, направлен по оси вращения и определяется по формуле:

| 1.4 |
| Момент импульса орбитальный тела | Определяется как векторное произведение радиус-вектора центра инерции тела на его полный импульс:

| 1.4 |
| Момент импульса орбитальный м.т. | 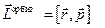
| 1.4 |
| Момент инерции | Физическая величина, количественно характеризующая инертность твёрдого тела, проявляющуюся во вращательном движении. | 1.4 |
| Момент инерции материальной точки |

| 1.4 |
| Момент инерции твердого тела относительно оси вращения |
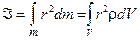
| 1.4 |
| Момент инерции тонкого прямого стержня | Относительно оси Z, проходящей через центр инерции стержня,
 Если ось Z проходит через конец стержня, то момент инерции равен
Если ось Z проходит через конец стержня, то момент инерции равен

| 1.4 |
| Момент инерции сплошного шара | Относительно оси Z, проходящей через центр инерции шара,

| 1.4 |
| Момент инерции сплошного диска | Относительно оси, перпендикулярной плоскости обруча и проходящей через центр инерции диска,
 Если ось Z совпадает с диаметром диска, то момент инерции равен
Если ось Z совпадает с диаметром диска, то момент инерции равен

| 1.4 |
| Момент инерции обруча (обода) | Относительно оси Z, перпендикулярной плоскости обруча и проходящей через центр инерции обруча,
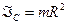 Если ось Z совпадает с диаметром обруча, то момент инерции равен
Если ось Z совпадает с диаметром обруча, то момент инерции равен

| 1.4 |
| Момент инерции полого тонкостенного цилиндра | Относительно оси Z, совпадающей с продольной осью симметрии цилиндра,
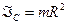
| 1.4 |
| Момент силы | Является количественной характеристикой быстроты изменения момента импульса | 1.4 |
| Момент силы относительно точки | Относительно точки О равен:
 , ,
| 1.4 |
| Момент силы относительно оси | Относительно оси Z создается только касательной составляющей силы:
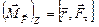 . .
| 1.4 |
| Мощность | Характеризует быстроту совершения работы или быстроту изменения энергии:
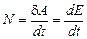
| 1.6 |
| Мощность в линейных параметрах | В стационарных силовых полях
в поступательном движении
 . .
| 1.6 |
| Мощность в угловых параметрах | В стационарных силовых полях
во вращательном движении
 . .
| 1.6 |
| Одномерность времени | См. Время - одномерность | |
| Однородность времени | См. Время - однородность | |
| Однородность пространства | См. Пространство - однородность | |
| Относительность движения | Любое движение (в том числе и механическое), как и вообще любое изменение, – относительно. Можно говорить лишь о взаимном перемещении тел. Про одно и то же тело можно сказать: движется прямолинейно, покоится, движется криволинейно и т.д., и все суждения будут верны, но с разных точек зрения. Состояние движения или покоя нельзя рассматривать безотносительно. Состояние движения тел можно описывать только по отношению к какому-нибудь другому телу | 1.1 |
| Перемещение линейное -вектор | Перемещение м.т. за время 
 Полное линейное перемещение равно геометрической (т.е. векторной) сумме отдельных перемещений м.т.
Полное линейное перемещение равно геометрической (т.е. векторной) сумме отдельных перемещений м.т.
| 1.2 |
| Плоскостность пространства | См. Пространство - плоскостность | |
| Полярные векторы | См. Векторы полярные | |
| Преобразования Галилея | Если инерциальные системы отсчета К и К ' движутся относительно друг друга вдоль оси абсцисс со скоростью  , то
t = t ', x = x ' + v x t,
y = y', , то
t = t ', x = x ' + v x t,
y = y', 
| 1.3 |
| Преобразования Лоренца (релятивистские) |
К ' ®К
x = g(x' + vt'), y = y', z = z',  ; ;
| 3.1 |
| Принцип запрета | Законы сохранения проявляются как принципы запрета: любое явление, при котором не выполняется хотя бы один из законов сохранения, запрещено, и в природе такие явления никогда не наблюдаются. Всякое явление, при котором не нарушается ни один закон сохранения, в принципе может происходить | 1.7 |
| Принцип относительности Галилея | Все механические явления в инерциальных системах отсчета протекают одинаково при скоростях намного меньших скорости света в вакууме (законы динамики одинаковы во всех ИСО). | 1.3 |
| Принцип относительности Эйнштейна (релятивистский) | Объединяет принцип относительности Галилея с принципом предельности и постоянства скорости света: все законы природы должны быть одинаковы в системах, движущихся прямолинейно и равномерно друг относительно друга. Всякий общий закон природы должен быть таким, чтобы сохранял свой вид при замене пространственно-временных переменных х, у, z, t первоначальной системы координат К новыми пространственно-временными переменными х', у', z', t' другой cистемы координат К'; при этом математическая связь между штрихованными и нештрихованными величинами определяется преобразованиями Лоренца. | 3.1 |
| Принцип предельности и постоянства скорости света | См. Закон распространения света | |
| Принцип эквивалентности | Каждая масса является одновременно и инертной и гравитационной. | 1.3 |
| Пространство | Совокупность отношений, выражающих взаимное расположение объектов – расстояния и ориентацию. | 1.1 3.1 |
| Пространство - однородность | Все точки пространства равноправны (пространство инвариантно по отношению к параллельному переносу) | 1.1 3.1 |
| Пространство - изотропность | Все направления равноправны (пространство инвариантно по отношению к повороту). | 1.1 3.1 |
| Пространство -плоскостность | Пространство подчиняется геометрии Евклида. | 1.1 3.1 |
| Пространство - трехмерность | Место события описывается тремя числами (координатами). | 1.1 3.1 |
| Псевдовекторы | См. векторы аксиальные | |
| Путь | Расстояние, пройденное м.т. по траектории, равное арифметической (скалярной) сумме длин отдельных перемещений, взятых вдоль траектории. | 1.2 |
| Работа | Скалярная физическая величина, характеризующая изменение энергии:
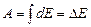 . .
| 1.6 |
| Работа в линейных параметрах | работа силы  на пути на пути  равна (в линейных характеристиках) равна (в линейных характеристиках)
 . .
| 1.6 |
| Работа в угловых параметрах | работа при повороте, характеризуемом вектором углового перемещения  , равна (в угловых характеристиках) , равна (в угловых характеристиках)
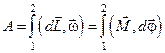 . .
| 1.6 |
| Сила | Векторная физическая величина, характеризующая быстроту изменения - как по величине, так и по направлению - импульса тела в результате взаимодействия данного тела с другими телами или полями:
 . .
| 1.3 |
| Силагравитационного взаимодействия точечных масс | См. Закон всемирного тяготения | 1.3 |
| Силагравитационного взаимодействия в однородном поле тяготения |

| 1.3 |
| Силы потенциальные | Определяются конфигурацией системы, т. е. взаимным расположением ее частей. См. также силы консервативные | 1.3 |
| Силы фундаментальные | Все реальные силы в природе сводятся к четырем фундаментальным силам, которые, в свою очередь, характеризуют четыре фундаментальных взаимодействия
1. Гравитационное взаимодействие ( , R ~ ¥).
2. Слабое взаимодействие( , R ~ ¥).
2. Слабое взаимодействие(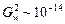 , R ~ 10–18 м).
3. Электромагнитное взаимодействие ( , R ~ 10–18 м).
3. Электромагнитное взаимодействие ( , R ~ ¥).
4. Сильное, или ядерное, взаимодействие ( , R ~ ¥).
4. Сильное, или ядерное, взаимодействие (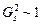 , R ~ 10–15 м). , R ~ 10–15 м).
| 1.3 |
| Сила тяжести | См. силугравитационного взаимодействия в однородном поле тяготения | |
| Сила упругая | См. Закон Гука | |
| Силы неконсервативные гироскопические | Зависят от величины и направления вектора скорости (например, магнитная сила Лоренца  ). ).
| 1.3 |
| Силы неконсервативные диссипативные | Действие этих сил сопровождается рассеиванием энергии, например, сила трения. | 1.3 |
| Силы инерции | 
| 1.3 |
| Силы инерции в поступательно движущихся НИСО |

| 1.3 |
| Силы инерции во вращающихся НИСО | 
| 1.3 |
| Сила инерции Кориолиса |

| 1.3 |
| Силы консервативные | Работа этих сил по замкнутой траектории равна нулю, т. е. их работа не сопровождается рассеиванием энергии | 1.3 |
| Система замкнутая | Система называется замкнутой, если на нее не действуют внешние силы. система может считаться замкнутой (в условиях данной задачи), если: - внешние силы есть, но векторная сумма всех внешних сил равна нулю; - векторная сумма всех внешних сил не равна нулю, но внутренние силы взаимодействия превосходят внешние; - если внешние силы не меньше внутренних, но время их действия мало по сравнению со временем действия внутренних сил. | 1.5 1.7 |
| Система материальных точек | Совокупность нескольких тел, каждое из которых можно считать м.т. | 1.5 |
| Система отсчета | Система координат, связанная с телом отсчета и служащая для указания положения тела в пространстве, вместе с часами, служащими для указания времени. | 1.3 |
| Система отсчета гелиоцентрическая | Инерциальная система отсчета, связанная с Солнцем. | 1.3 |
| Система отсчета геоцентрическая | Инерциальная система отсчета, связанная с Землей. | 1.3 |
| Система отсчета инерциальная (ИСО) | Класс таких СО, для которых все физические законы имеют совершенно одинаковый вид, или, как принято говорить в физике, являются инвариантными относительно перехода из одной СО в другую. Их названия происходят от того, что во всех ИСО выполняется, в частности, первый закон Ньютона - закон инерции. | 1.3 |
| Система отсчета лабораторная | См. ИСО | |
| Система отсчета неинерциальная | Системы отсчета, которые движутся ускоренно по отношению к ИсО. | 1.3 |
| Скорость | Векторная физическая величина, которая показывает быстроту и направление движения тела. | 1.2 |
| Скорость линейная (мгновенная) | 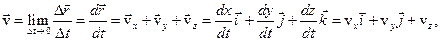
| 1.2 |
| Скорость линейная (мгновенная) при траекторном описании |

| 1.2 |
| Скорость линейная (средняя) | 
| 1.2 |
| Скорость линейная модуль | 
| 1.2 |
| Скорость угловая (мгновенная) | 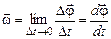
| 1.2 |
| Скорость угловая (средняя) |
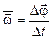
| 1.2 |
| Сплошная среда | Эта модель применяется в случае, когда нельзя не учитывать деформаций и перемещений частей тела. В сплошной среде существенную роль играют внутренние перемещения в теле. | 1.1 |
| Твердое тело | см. Абсолютно твердое тело | |
| Тело отсчета | Тело (совокупность тел), по отношению к которому описывается движение данного тела. | 1.3 |
| Теорема Штейнера | Момент инерции Áтела относительно произвольной оси есть сумма момента инерции ÁС относительно параллельной оси, проходящей через центр инерции тела, и произведения массы m тела на квадрат расстояния d между осями: Á = ÁС + md 2. | 1.4 |
| Теория относительности (специальная) Эйнштейна | (см. принцип относительности Эйнштейна) | 3.1 |
| Траектория | Пространственная линия, описываемая уравнениями: а) в трехмерном пространстве – L (x,y,z) = 0 или б) на плоскости – y = y (x). В каждой точке траектории в трехмерном пространстве задаются шесть чисел – три координаты и три проекции скорости (импульса). | 1.2 |
| Трехмерность пространства | См. Пространство - трехмерность | |
| Угол поворота - вектор | Угол поворота радиуса окружности, по которой двигается любая точка а.т.т. при простом вращательном движении.
Длина вектора  угла поворота численно равна углу угла поворота численно равна углу  в радианах, а направление совпадает с направлением оси вращения в соответствии с правилом правого винта в радианах, а направление совпадает с направлением оси вращения в соответствии с правилом правого винта
| 1.2 |
| Угловое перемещение - вектор | Модуль  вектора углового перемещения вектора углового перемещения  численно равна величине изменения угла поворота численно равна величине изменения угла поворота  в радианах, а направление совпадает с направлением оси вращения в соответствии с правилом правого винта. в радианах, а направление совпадает с направлением оси вращения в соответствии с правилом правого винта.
| 1.2 |
| Удар абсолютно упругий | При центральном и прямом ударе сохраняются полный импульс и механическая энергия:
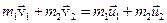
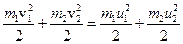
| 1.7 |
| Удар абсолютно неупругий | При центральном и прямом ударе сохраняются полный импульс и полная энергия:

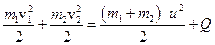
| 1.7 |
| Удар центральный | Центры инерции шаров лежат на линии удара | 1.7 |
| Удар прямой | Векторы скорости  центров инерции шаров в начале удара направлены параллельно линии удара. центров инерции шаров в начале удара направлены параллельно линии удара.
| 1.7 |
| Уравнения поступательного движения кинематические в координатной форме | См. Движение поступательное – уравнения кинематические в координатной форме | |
| Уравнения поступательного движения равнопеременного кинематические в координатной форме | См. Движение поступательное равнопеременное – уравнения кинематические в координатной форме | |
| Уравнения равномерного поступательного движения кинематические в координатной форме | См. Движение поступательное равномерное – уравнения кинематические в координатной форме | |
| Уравнения поступательного движения кинематические в векторной форме | См. Движение поступательное – уравнения кинематические в векторной форме | |
| Уравнения поступательногодвижения равнопеременного кинематические в векторной форме | См. Движение поступательное раавнопеременное – уравнения кинематические в векторной форме | |
| Уравнения поступательногодвижения равномерного кинематические в векторной форме | См. Движение поступательное равномерное – уравнения кинематические в векторной форме | |
| Уравнения поступательного движения кинематические в траекторной форме | См. Движение поступательное – уравнения кинематические в траекторной форме | |
| Уравнения поступательного движения равнопеременного кинематические в траекторной форме | См. Движение поступательное равнопеременное – уравнения кинематические в траекторной форме | |
| Уравнения поступательного движения равномерного кинематические в траекторной форме | См. Движение поступательное равномерное – уравнения кинематические в траекторной форме | |
| Уравнения вращательного простого движения кинематические в координатной форме | См. Движение вращательное простое - уравнения кинематические в координатной форме | |
| Уравнения вращательного простого движения равнопеременного кинематические в координатной форме | См. Движение вращательное простое равнопеременное - уравнения кинематические в координатной форме | |
| Уравнения вращательного простого движения равномерного в координатной форме | См. Движение вращательное простое равномерное - уравнения кинематические в координатной форме | |
| Уравнения вращательногопростого движения в векторной форме | См. Движение вращательное простое - уравнения кинематические в векторной форме | |
| Уравнения вращательногопростого движения равнопеременного в векторной форме | См. Движение вращательное простое равнопеременное - уравнения кинематические в векторной форме | |
| Уравнения вращательногопростого движения равномерного в векторной форме | См. Движение вращательное простое равномерное - уравнения кинематические в векторной форме | |
| Ускорение | В физике определяется как быстрота изменения скорости. | 1.2 |
| Ускорение линейное (мгновенное) |  
| 1.2 |
| Ускорение линейное (мгновенное) при траекторном описании | 
| 1.2 |
| Ускорение линейное (среднее) | 
| 1.2 |
| Ускорение - модуль вектора | 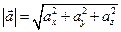 или или 
| 1.2 |
| Ускорение свободного падения эффективное | 
| 1.3 |
| Ускорение угловое | Векторная физическая величина, определявшая быстроту изменения угловой скорости. | 1.2 |
| Ускорение угловое (мгновенное) | 
| 1.2 |
| Ускорение угловое (среднее) | 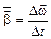
| 1.2 |
| Ускорение тангенциальное | Характеризует быстроту изменения скорости по модулю:

| 1.2 |
| Ускорение нормальное (центростремительное) | Характеризует быстроту изменения скорости по направлению:
 . .
| 1.2 |
| Физика | Происходя от греческого "физис" (природа), представляет собой в широком смысле слова науку о природе, т.е. естествознание. физика изучает наиболее общие формы существования материи - пространство и время, а также наиболее общие формы ее движения (механическое, волновое, квантовое движения и другие, возможно еще не открытые). физика есть та часть естествознания, которая может быть выражена языком математических формул (А.Эйнштейн). | 1.1 |
| Формула Эйнштейна для полной энергии | См. Энергия полная – формула Эйнштейна | 3.1 |
| Центр инерции | положение центра масс (инерции) твердого тела или системы материальных точек определяется по формуле
 . .
| 1.5 |
| Центр масс | См. центр инерции | |
| Часы | Любое физическое явление, которое может быть воспроизведено любое необходимое количество раз. | 1.1 3.1 |
| Число степеней свободы | Число уравнений движения, необходимое и достаточное для описания движения какой-либо системы м.т. или т.т.. Эти уравнения должны описывать движение системы вполне однозначно, но среди них не должно быть уравнений, являюшихся следствием других.
число степеней свободы i меньше  на число f независимых жестких связей между м.т.:
i = на число f независимых жестких связей между м.т.:
i =   f f
| 1.1 |
| Энергия | Энергия – скалярная физическая величина, являющаяся полной и наиболее общей характеристикой состояния системы. | 1.7 |
| Энергия внутренняя | Является одновременно и энергией покоя:
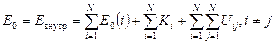 . .
| 1.7 |
| Энергия кинетическая | Это скалярная физическая величина, количественно характеризующая запас движения, которое может превращаться в другой вид движения, а энергия, соответственно, – в другую, например – в потенциальную энергию. Это отличает кинетическую энергию от импульса, который характеризует только запас движения. Кинетическая энергия – величина арифметическая, неотрицательная. | 1.7 |
| Энергия кинетическая в линейных параметрах | 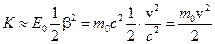
| 1.7 |
| Энергия кинетическая релятивистская в линейных параметрах | 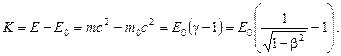
| 3.1 |
| Энергия кинетическая в угловых параметрах | 
| 1.7 |
| Энергия механическая | Кинетическая и потенциальная энергии в сумме составляют механическую энергию. Е мех = K + U | 1.7 |
| Энергия покоя | В системе центра масс m = m 0 – масса покоя, а Е = Е 0 = m 0 c 2 – энергия покоя. | 3.1 |
| Энергия полная | Определяется как сумма: E = K + U + E внутр. | 1.7 |
| Энергия полная – формула Эйнштейна | Для свободной частицы: Е = mc 2. | 3.1 |
| Энергия потенциальная | Скалярная физическая величина, характеризующая взаимодействие тел с другими телами или с полями. Потенциальная энергия характеризует скрытый запас энергии, который определяется конфигурацией системы, то есть взаимным расположением частей системы. | 1.7 |
| Энергия потенциальная упругой деформации | 
| 1.3 1.7 |
| Энергия потенциальная взаимодействия точечных масс | 
| 1.7 |
| Энергия потенциальная в однородном поле тяготения | U = mgy. | 1.7 |
| Энергия связи | Энергия, которая выделяется при образовании устойчивых систем
∆ Е = ∆ m × c 2,
Здесь
 – дефект массы.
– дефект массы.
| 1.7 |






