υ = λν. (12)
Из формулы (11) следует, что λ = 2λст, тогда
υ = 2λст ν. (13)
По формуле (13) можно рассчитать скорость звука при температуре эксперимента.
Зависимость скорости звука от температуры описывается соотношением
υ = υ 0 
, (14)
где υ 0 – скорость звука при 0 ºС, t – температура в ºС, α – температурный коэффициент объемного расширения газа. Для воздуха α = (3,67 ± 0,05)·10–3 ºС–1. Из формулы (14) выразим скорость звука при 0 ºС:
υ 0 = 
. (15)
Подставив (13) в (15), получим расчетную формулу:
υ 0 = 
. (16)
Упрощенное описание установки и процессов, в ней происходящих
Установка для определения скорости звука (рис. 2) состоит из резонатора 1, звукового генератора 2, осциллографа 3 и отсчетной линейки 4. Резонатор представляет собой закрытую с обоих торцов трубу, в которую вмонтирован телефон 5 и подвижный шток 6 с микрофоном 7. Звуковой генератор создает электрические колебания определенной частоты. Телефон преобразует эти колебания в звуковые колебания той же частоты. Звуковая волна от телефона распространяется внутри резонатора. В результате интерференции прямой и отраженной звуковой волны в резонаторе возникает стоячая волна, которая представляет собой чередующиеся сгущения и разрежения воздуха.
На рис. 2 условно изображена стоячая волна, пучностям которой соответствует наибольшая амплитуда. Звук улавливается микрофоном и преобразуется в электрический сигнал, подаваемый на осциллограф. На экране осциллографа наблюдается сигнал синусоидальной формы, амплитуда которого пропорциональна амплитуде звуковых колебаний в данном месте резонатора. Когда мембрана микрофона находится в пучностях стоячей волны, амплитуда воспринимаемых колебаний максимальна, а когда в узлах – минимальна.
На опыте обычно измеряют положение первого максимума x 1 и последнего максимума x k и рассчитывают длину стоячей волны по формуле
λст = 
, (17)
где k – число максимумов.
В несколько более точном представлении схема эксперимента и происходящие в ней явления выглядит иначе. Диаметр микрофона равен внутреннему диаметру резонатора. Таким образом, между микрофоном и телефоном существует замкнутое пространство, в котором распространяются падающая и отраженная волны. Стоячие волны возникают в том случае, когда между мембранами телефона микрофона укладывается целое число длин волн λст и возникает явление резонанса, отчетливо воспринимаемое на слух и регистрируемое осциллографом.
Порядок выполнения работы
1. Включить звуковой генератор и установить частоту колебаний по указанию преподавателя (рекомендуемые частоты 900, 1000, 1100 Гц).
2. Перемещая шток с микрофоном по направлению от источника колебаний, определить число максимумов k с помощью осциллографа. По отсчетной линейке найти положение первого максимума x 1 и последнего максимума x k. Результаты измерений занести в таблицу.
Таблица
Результаты измерений и вычислений
| № п/п | n, Гц | k | x 1 | x k | lст | υ 0, м/с |
3. Для каждого значения частоты выполнить не менее трех измерений. При этом каждый раз рекомендуется заново устанавливать частоту на звуковом генераторе.
4. По формуле (17) рассчитать длину стоячей волны, а по формуле (16) – скорость звука в воздухе при 0 ºС. Результаты вычислений записать в таблицу.
5. Рассчитать приближенное значение скорости звука и оценить случайную погрешность D υ сл по методу Стьюдента.
6. Вычислить приборную погрешность в скорости звука D υ сист. Относительная приборная погрешность рассчитывается по формуле
,
где Dlст принять равной цене деления отсчетной линейки, Dn = 20 Гц, D t принять равной половине цены деления шкалы термометра,
Da = 5×10–5 ºС –1. Абсолютная приборная погрешность будет равна
D υ сист = e υ 0.
7. Определить общую погрешность по формуле
D υ = 
.
8. Записать окончательный результат с указанием погрешности определения.
9. Рассчитать по формуле (1) скорость звука в воздухе
(γ = 1,40; М = 29·10–3 кг/моль) и сравнить с полученным на опыте значением.
10. Сделать выводы по работе.
Контрольные вопросы и задания
1. Что такое звук? Каков диапазон частот звуковых волн? От чего зависит скорость звука?
2. Может ли звук распространяться в вакууме? Ответ обоснуйте.
3. Запишите уравнение бегущей волны и поясните величины, входящие в уравнение.
4. Дайте определение стоячей волны. Как возникают стоячие волны?
5. Выведите уравнение стоячей волны.
6. Что такое узлы и пучности? Получите уравнения координат узлов и пучностей.
7. В чем отличие стоячей волны от бегущей?
8. Построить график стоячей волны для фиксированного момента времени
t = 0, T /8, T /4, 3 T /8 или T /2 (или для других моментов по указанию преподавателя).
9. Обоснуйте расчетную формулу для скорости звука.
10. Опишите экспериментальную установку и методику определения скорости звука.
Литература
1. Савельев И. В. Курс общей физики: Учебн. пособие для втузов: в 3 т. Т.1: Механика. Молекулярная физика. - 3-е изд., испр. - М.: Наука, 1986. – 432с.
2. Детлаф А. А., Яворский Б. М. Курс физики: Учебн. пособие для втузов. - М.: Высшая школа, 1989. - 607 с. - предм. указ.: с. 588-603.
3. Майсова Н.Н. Практикум по курсу общей физики. – М.: Высшая школа, 1970
4. Лабораторный практикум по физике: Учеб. пособие для студентов втузов./ Ахматов А.С., Андреевский В.М., Кулаков А.И. и др.; Под редакцией А.С. Ахматова. – М.: Высшая школа. 1980. – 360 с.
Часть III. Молекулярная физика, термодинамика, явления переноса
ОПРЕДЕЛЕНИЕ ОТНОШЕНИЯ ТЕПЛОЕМКОСТЕЙ
ПО МЕТОДУ КЛЕМАНА И ДЕЗОРМА
Цель работы – определить отношение теплоемкостей 
для воздуха.
Приборы и принадлежности – стеклянный баллон емкостью около 25 литров с краном, манометр, насос, соединительные трубки.
Теоретическое введение
Удельной теплоемкостью вещества называется физическая величина, равная количеству теплоты, необходимой для нагревания единицы массы вещества на 1 оС(К) в данном процессе.
Молярной теплоемкостью вещества называется физическая величина, равная количеству теплоты, необходимой для нагревания одного моля вещества на 1оС(К) в данном процессе.
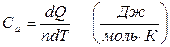
Очевидно, 
где 
молярная масса вещества.
Для газов принято различать теплоемкость при постоянном объеме Сvи при постоянном давлении Cp, в зависимости от процесса нагревания газа.
Согласно первому закону термодинамики количество переданной системе теплоты расходуется на увеличение внутренней энергии системы и работу расширения
dQ=dU+dA
При нагревании газа при V=const работа расширения dA=0, и все тепло идет на увеличение внутренней энергии, т.е. на нагревание газа.
При нагревании газа при P =const тепло затрачивается не только на нагревание, но и на работу расширения газа. Поэтому Сp > Сv.
Согласно кинетической теории идеального газа
где z – число степеней свободы молекулы
n – число молей газа
T –температура по шкале Кельвина
R – универсальная газовая постоянная
Соответственно: для двухатомного газа z = 5 и γ = 1,40; для многоатомного z = 6 и γ = 1,33.
Для экспериментального определения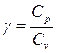 
воздуха в данной работе используется адиабатический процесс расширения или сжатия.
Адиабатическим процессом называется процесс без теплового обмена с окружающей средой. dQ = 0
Первое начало термодинамики для адиабатического процесса запишется как
0=dU+dA
или
а) dU = – dA - увеличение внутренней энергии газа (нагревание) происходит за счет работы внешних сил, совершающих сжатие газа.
б) dA = – dU – работа расширения, совершаемая газом, происходит за счет уменьшения его внутренней энергии.
Таким образом, при адиабатическом сжатии газ нагревается, при адиабатическом расширении – охлаждается.
Для осуществления адиабатического процесса нужно либо теплоизолировать систему, либо вести процесс так быстро, чтобы теплообмен не успел произойти.
Описание установки.
Стеклянный баллон А емкостью 25 литров с пробкой q соединен резиновыми трубками с насосом N и манометром М. На трубке, соединяющей баллон с насосом, имеется кран К (см. рис. 1).
Проведение эксперимента
I. Определение 
при сжатии воздуха.
1) Перед опытом открыть пробку q. Давление воздуха в баллоне А станет равным атмосферному давлению, и жидкость в манометре установится на одном и том же уровне в обоих коленах.
2) Закрыть трубку сосуда пробкой q, открыть кран К и осторожно накачать при помощи насоса N некоторое количество воздуха. Уровень жидкости в левом (соединенном с баллоном) колене начинает при этом опускаться, а в правом – подниматься.
Накачивать воздух следует до тех пор, пока разность высот уровней жидкости в манометре не достигнет нескольких десятков сантиметров (25 – 30 см). (При накачивании воздух в баллоне сжимается, и температура его повышается).
3) Закрыть кран К и дать воздуху в баллоне охладиться до комнатной температуры. Так как при охлаждении газа в баллоне его давление понижается, то разность уровней жидкости в манометре несколько уменьшается. Когда температура в баллоне станет равной температуре окружающего воздуха, перемещение уровней жидкости в манометре прекратится, и установится определенная разность высот h1, которую отмечают по шкале манометра. Давление внутри баллона будет равно
P1 = H + h1,
где Н – атмосферное давление. Удельный объем газа (объем, занимаемый единицей массы газа) в баллоне будет V1, а температура t1 = tкомн. Это состояние изобразится точкой Ана графике, приведенном в таблице 1.
4). Открыть и очень быстро закрыть пробку q. При этом с воздухом в баллоне произойдут два следующие друг за другом процесса:
а). В момент открытия пробки происходит быстрое расширение воздуха, заключенного в баллоне, которое можно считать адиабатическим из-за его кратковременности. Давление при этом упадет до атмосферного и будет равно Р2 = Н объем возрастает до V2, так как часть воздуха вышла, и на единицу массы теперь приходится больший объем. Температура становится ниже комнатной t2 < t1, так как воздух адиабатически расширился. Это второе состояние изображается на графике, приведенном в таблице 1, точкой В.
б). После закрытия пробки q через 2 – 3 минуты воздух в баллоне в результате теплообмена снова нагревается до комнатной температуры tк. В процессе теплообмена происходит изохорическое нагревание воздуха, так как удельный объемV2 остается неизменным. При этом давление воздуха возрастает до
Р3 =Н + h2.
Разность уровней h2 (после того, как она установится) снова отмечают по шкале манометра. Это третье состояние газа изобразится точкой С (см. тот же график и таблицу).
Состояниям А и С соответствует одна и та же температура, поэтому на графике эти точки можно соединить изотермой.
Таблица трех состояний в процессе работы не заполняется, она нужна для вывода расчетной формулы.
Таблица 1
Три состояния воздуха при сжатии и графики соответствующих переходов
| При каких условиях | Состоя- ние | Уд. объем | Давле- ние | Темпе- ратура |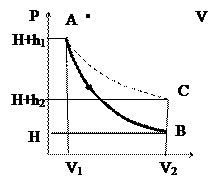 
|
| До откры- тия пробки | А | V1 | H +h1 | tк | |
| В момент открытия пробки | В | V2 | H | t2 | |
| После закрытия пробки | С | V2 | H + h2 | tк |
Таблица 2
Три состояния воздуха при расширении и графики соответствующих переходов
| При каких условиях | Состоя- ние | Уд. объем | Давле- ние | Темпе- ратура | 
|
| До откры- тия пробки | А | V1 | H – h1 | tк | |
| В момент открытия пробки | В | V2 | H | tк | |
| После закрытия пробки | С | V2 | H – h2 | tк |
Вывод расчетной формулы
Рассматривая переход воздуха из состояния А в состояние В как процесс адиабатический, применим к нему уравнение Пуассона
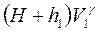
или 
(1)
Переход от конечного состояния С к начальному состоянию А можно было бы произвести изотермически, так как температура в обоих состояниях одинаковая – tk ..
Применим к этому переходу закон Бойля-Мариотта
(2)
Возводя левую и правую части уравнения (2) в степень γ, получим
(3)
Левые части равенств (1) и (3) равны, следовательно, равны и правые
(4)
Логарифмируя (4), получим
откуда
или 
Вычитая и прибавляя в знаменателе последнего выражения ln H, получим
Из теории рядов известно, что выражение 
может быть представлено в виде
Если Х мало, то ln 
В нашем случае
– достаточно малы и
Формула (5) позволяет определить величину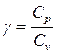 
по двум показаниям манометра h1 и h2.Опыт следует провести не менее пяти раз при различных показаниях для случаев расширения и сжатия воздуха в баллоне. Результаты измерений h1 и h2 занести в таблицу 3. Для каждой пары h1 и h2 по формуле (5) вычислить γ, полученные значения занести в таблицу. Вычислить приближенное значение γ, абсолютную и относительную погрешности. Окончательный результат записать в виде
Таблица 3
Результаты измерений и вычислений
| № п/п | h1 | h2 | 
| |
| Сжатие | ||||
| Расширение |
Приближенное значение γпр
Абсолютная погрешность ∆γ
Контрольные вопросы
1. Что называется удельной и молярной теплоемкостями? Соотношение между ними. Единицы измерения.
2. Что такое Сv и что такое Ср? Почему Ср > Сv?
3. Какой процесс называется адиабатическим? Как практически можно осуществить адиабатический процесс?
4. Пользуясь первым началом термодинамики и уравнением Менделеева-Клапейрона, обосновать закон Пуассона для адиабатического процесса.
5. В системе координат Pи V представьте адиабату и сопоставьте с изотермой. Почему адиабата идет более круто, чем изотерма?
6. Выведите расчетную формулу Клемана и Дезорма. Какие изопроцессы имели место в данной работе?
7. Проанализировать таблицы 1 и 2 для расширения и сжатия и выяснить физический смысл процессов.
Литература
1. Савельев И. В. Курс общей физики: Учебн. пособие для втузов: в 3 т. Т.1: Механика. Молекулярная физика. - 3-е изд., испр. - М.: Наука, 1986. – 432с.
2. Детлаф А. А., Яворский Б. М. Курс физики: Учебн. пособие для втузов. - М.: Высшая школа, 1989. - 607 с. - предм. указ.: с. 588-603.
3. Зисман Г. А., Тодес О. М.. Курс общей физики для втузов: в 3 т. Т. 1: Механика, молекулярная физика, колебания и волны - 4-е изд., стереотип. - М.: Наука, 1974. - 340 с.
4. Методические указания к выполнению лабораторных работ по разделу “Механика“.- Иваново, ИХТИ, 1989 г. (под редакцией Биргера Б.Н.).
ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ВЯЗКОСТИ ЖИДКОСТИ
Цель работы – в работе требуется определить коэффициент вязкости глицерина по методу Стокса.
Приборы и принадлежности: труба с глицерином, масштабная линейка, шарики, микрометр и секундомер.
Теоретическое введение.
Если привести один слой жидкости в упорядоченное движение со скоростью u1, то он увлечет за собой прилегающий слой со скоростью u2, последующий со скоростью u3 и т.д. При этом скорость упорядоченного движения убывает в перпендикулярном направлении к движению слоев жидкости, т.е. u1>u2>u3…. Выделим два слоя жидкости на расстоянии Dx друг от друга, движущихся со скоростями 
и 
(см. рис.1).
Вследствие передачи импульса при переходе молекул из слоя в слой возникает сила внутреннего трения.
Сила внутреннего трения пропорциональна площади соприкосновения взаимодействующих слоев жидкости и градиенту скорости
, (1)
где 
- коэффициент динамической вязкости жидкости (или просто вязкость); S - площадь слоя; 
- градиент скорости.
Коэффициентом динамической вязкости называется величина, численно равная силе внутреннего трения, с которой один слой увлекает или тормозит другой слой жидкости при условии, что площадь соприкосновения слоев 
и градиент скорости 
.
В системе СИ за единицу динамической вязкости принимают 
- вязкость такой среды, в которой один слой увлекает или тормозит другой с силой в 
, если площадь соприкосновения слоев 
и градиент скорости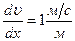 
.
Коэффициентом кинематической вязкости 
называется отношение коэффициента динамической вязкости к плотности жидкости
. (2)
Коэффициент вязкости существенно зависит от температуры. Для жидкости с повышением температуры он резко уменьшается.
Определение коэффициента динамической вязкости методом Стокса
Рассмотрим свободное падение тела внутри покоящейся жидкости. Пусть в сосуде с жидкостью вертикально падает небольшой шарик радиуса 
с малой скоростью 
(см. рис. 2). В этом случае между тонким слоем жидкости, обволакивающим шарик, и окружающей средой возникает сила внутреннего трения. Последняя направлена против движения и, согласно закону Стокса, равна
, (3)
где - коэффициент вязкости жидкости.
Кроме указанной силы 
, на шарик действуют две силы – сила тяжести 
(вертикально вниз) и сила Архимеда 
(вертикально вверх).
В первый момент падения шарик движется равноускоренно, так как сила тяжести больше суммы сил, действующих вертикально вверх. При дальнейшем падении скорость шарика увеличивается, возрастает и сила внутреннего трения (см. формулу 3). Когда скорость шарика будет иметь такое значение, при котором все три силы 
, и уравновешиваются (сумма сил равна нулю), тогда шарик согласно первому закону Ньютона, будет падать равномерно с постоянной скоростью 
.
Для этого случая имеем
. (4)
Обозначим через 
плотность шарика, а через 
- плотность жидкости. Если силу тяжести выразить через плотность, то получим
. (5)
Соответственно сила Архимеда
. (6)
Подставляя значения сил (3), (5) и (6) в (4) и выражая , найдем
. (7)
По формуле (7) можно вычислить коэффициент вязкости жидкости, если измерить на опыте скорость равномерного движения шарика в жидкости. Для этой цели необходимо измерить время t прохождения шариком расстояния l между метками m и n (см. рис.2). Скорость равномерного движения будет 
, и расчетная формула примет вид
. (8)
Порядок выполнения работы
1. При помощи микрометра измерить пять-шесть раз диаметр шарика, вычислить из полученных данных среднее значение и занести в таблицу радиус шарика. Аналогично найти радиусы еще четырех шариков.
2. Выбрать расстояние между метками m и n
3. По секундомеру отметить время движения каждого шарика от верхней до нижней метки.
4. По формуле (8) рассчитать коэффициент вязкости глицерина для каждого опыта, результаты занести в таблицу.
5. Вычислить приближенное значение коэффициента вязкости h, абсолютную и относительную погрешности.
6. Окончательный результат записать в виде
.
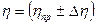Таблица
Результаты измерений и вычислений
| № п/п | Радиус шарика r, м | Время падения шарика t, с | Расстояние между метками l, м | Коэффициент вязкости
h,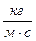 
|
Приближенное значение 
| ||||
Абсолютная погрешность 
|
Контрольные вопросы
1. Что называется коэффициентом вязкости? Единицы измерения вязкости.
2. От каких факторов зависит коэффициент вязкости жидкости?
3. Сущность метода Стокса для определения коэффициента вязкости жидкости с выводом расчетной формулы.
4. Обосновать изменение скорости движения шарика с увеличением его диаметра?
Литература
1. Детлаф А. А., Яворский Б. М. Курс физики: Учебн. пособие для втузов. - М.: Высшая школа, 1989. - 607 с. - предм. указ.: с. 588-603.
2. Лабораторный практикум по физике: Учеб. пособие для студентов втузов/ Б. Ф. Алексеев, К. А. Барсуков, И. А. Войцеховская и др.; Под ред. К. А. Барсукова и Ю. И. Уханова. – М.: Высш. школа,1988. – 351 с.: ил.
ISBN 5-06-001365-0
3. Трофимова Т.И. Курс физики. - М.: Высшая школа, 1990г.
ОПРЕДЕЛЕНИЕ СРЕДНЕЙ ДЛИНЫ СВОБОДНОГО ПРОБЕГА И ЭФФЕКТИВНОГО ДИАМЕТРА МОЛЕКУЛ ВОЗДУХА
Цель работы: определить среднюю длину свободного пробега и эффективный диаметр молекул воздуха по коэффициенту внутреннего трения.
Приборы и принадлежности: сосуд с капилляром, секундомер, мерный и химический стаканы, барометр.
Теоретическое введение
Молекулы газа, находясь в тепловом движении, непрерывно сталкиваются друг с другом (см. рис. 1). При нормальных условиях каждая молекула воздуха за одну секунду испытывает до 109 столкновений с другими молекулами (для упрощения задачи не будем принимать во внимание химический состав воздуха, а будем рассматривать некую эффективную молекулу). Под столкновением молекул подразумевают процесс взаимодействия между молекулами, в результате которого молекула изменяет направление своего движения.
Расстояние, проходимое молекулой между двумя последовательными столкновениями, называется длиной свободного пробега l.
Длина свободного пробега между отдельными столкновениями молекулы могут значительно отличаться друг от друга, поэтому вводят понятие средней длины свободного пробега <l>, которая определяется как отношение:
, (1)
где < v> и < z > – средняя скорость и среднее число столкновений молекулы в единицу времени.
Весьма приближенно число столкновений молекул за одну секунду можно подсчитать исходя из следующих соображений. Условно изобразим путь, пройденный молекулой за 1 с, прямой линией (рис. 2), длина которой численно равна < v>. Пусть в окружающем пространстве в единице объема содержится n молекул. Тогда рассматриваемая молекула, двигаясь по прямой, столкнется со всеми молекулами, центры которых лежат внутри цилиндра радиусом R, равным эффективному диаметру молекул d. Под эффективным диаметром понимается минимальное расстояние (рис. 3), на которое сближаются при столкновении центры двух молекул.
Так как объем цилиндра равен p R 2< v > = p d 2< v >, то всего молекул в нем окажется p d 2< v > n. С этими молекулами и произойдут столкновения за 1 с. Таким образом, < z > = p d 2< v > n.
Более точный расчет с учетом распределения Максвелла молекул по скоростям приводит к выражению:
. (2)
Подставив это значение < z > в (1) получим для средней длины свободного пробега следующую формулу:
. (3)
После замены p d 2 на эффективное сечение молекулы s, формула (3) принимает вид:
. (4)
При постоянной температуре концентрация n пропорциональна давлению p (n = p/kT). Следовательно, средняя длина свободного пробега обратно пропорциональна давлению:
. (5)
Эффективное сечение молекул уменьшается с повышением температуры по уравнению
(6)
где – s0 величина, которую можно рассматривать как истинный диаметр молекулы, С – константа.
В соответствии с уравнением (6) при повышении температуры длина свободного пробега увеличивается. При нормальных условиях средняя длина свободного пробега молекул в газе составляет величину порядка 10–7 м. При очень высоком вакууме соударений молекул между собой практически не происходит. Они ударяются только о стенки сосуда и длина пробега молекулы становится постоянной, равной линейным размерам сосуда.
Столкновения молекул, происходящие в газах в результате теплового движения молекул, определяют характер процессов, известных под названием явлений переноса. К этим процессам относятся диффузия, теплопроводность и внутреннее трение или вязкость.
Диффузией называется самопроизвольный процесс, возникающий при наличии градиента концентрации в системе, заключающийся в переносе массы в направлении убывания концентрации и совершающийся за счет теплового движения атомов, молекул, ионов, или более крупных агрегированных частиц. Диффундировать могут как растворенные в веществе посторонние частицы, так и частицы самого вещества (самодиффузия).
Теплопроводность – это процесс переноса теплоты внутри неравномерно нагретой среды ппри наличии градиента температуры и при условии, что конвекция и другие явления устранены. При этом молекулы, находящиеся в более нагретых областях и обладающие в среднем более высокой кинетической энергией, при хаотическом тепловом движении переносят энергию в более холодные области, в результате чего происходит выравнивание температуры по всей области.
Внутреннее трение или вязкость – это свойство жидкостей и газов оказывать сопротивление перемещению одной их части относительно другой. При переходе частиц (атомов, молекул, ионов) из одного слоя в другой, движущихся относительно друг друга с некоторой скоростью, они переносят с собой импульс, при этом слой, движущийся быстрее, замедляется, а слой, движущийся медленнее, ускоряется.
Все явления переноса формально могут быть описаны уравнением:
, (7)
где J – поток переносимой величины (массы, теплоты, импульса), k – коэффициент пропорциональности (диффузии D, теплопроводности k, внутреннего трения h), dJ/dn – градиент переносимой величины (концентрации, температуры, скорости) вдоль нормали к площадке D S, через которую осуществляется перенос величины J, t – время.
Молекулярно-кинетическая теория газов позволяет во всех деталях интерпретировать явления переноса и установить связь между коэффициентами переноса (диффузии, теплопроводности, вязкости):
(8)
, (9)
, (10)
где r – плотность вещества, СV – удельная теплоемкость газа при постоянном объеме.
Последнее уравнение положено в основу определения средней длины свободного пробега молекул воздуха в данной работе.
Из формулы (9) получаем:
(10)
Коэффициент вязкости, в свою очередь, можно определить из закона Пуазейля, описывающего ламинарное течение вязкой среды в тонкой цилиндрической трубке.
Согласно закону Пуазейля объем газа/жидкости, протекающей через поперечное сечение трубки под действием перепада давления на концах трубки D p, определяется выражением:
, (11)
где V – объем газа, r – радиус капилляра, l –длина капилляра, D p – разность давлений на концах капилляра, t – время, в течение которого через капилляр протекает данный объем газа.
Из (3) получаем:
. (12)
Все величины, входящие уравнение (12) легко измеряются в опыте.
Средняя арифметическая скорость молекул газа < v > согласно молекулярно-кинетической теории определяется выражением:
, (13)
где R – универсальная газовая постоянная, Т – абсолютная температура,
М – молярная масса.
Плотность газа r находится из уравнения Менделеева-Клапейрона:
, (14)
где P – давление газа.
После подстановки (12), (13) и (14) в (10) получаем:
. (15)
Разность давлений D P может быть рассчитана по формуле:
, (16)
где h 1 и h 2 – высоты уровней жидкости в сосуде А (рис. 4), g – ускорение свободного падения, rв – плотность воды.
Эффективный диаметр d молекулы находится из соотношения (3), в котором n – число молекул газа в единице объема при данных условиях. Для перехода к нормальным условиям (T 0 = 273,15 K, P 0= 760 мм рт.ст. или 1,01325×105 Па) воспользуемся соотношением:
, (17)
Из (3) и (17) получаем выражение для эффективного диаметра молекулы газа:
. (18)
Описание установки
Для определения средней длины свободного пробега и эффективного диаметра молекул воздуха используется установка, состоящая из сосуда, заполненного водой (1), капилляра (2) и мерного стакана (3) (рис. 1). Если открыть кран, то вода будет выливаться из сосуда, одновременно через капилляр в сосуд будет засасываться воздух. Таким образом, капилляр является той трубкой, в которой устанавливается ламинарное течение воздуха в результате того, что разные концы трубки находятся под разным давлением (верхний конец – под атмосферным давлением, нижний – меньше атмосферного). Сосуд снабжен шкалой, с помощью которой можно определить высоту столба вытекшей воды. Под сосудом устанавливается мерный стакан для определения объема вытекшей воды, равного объему воздуха, поступившего в сосуд.
Порядок выполнения работы
1. Поставить под сосуд химический стакан, открыть кран, прикрыв пальцем капилляр. Дождавшись, когда вода перестанет вытекать из сосуда, заменить химический стакан мерным стаканом.
2. Отметить по шкале начальную высоту уровня воды h 1 в сосуде, отпустить палец, освободив капилляр, и одновременно включить секундомер.
3. Через время t = 30 – 120 секунд (выбирается в зависимости от емкости сосуда и параметров капилляра) закрыть кран (4) и одновременно остановить секундомер.
4. Записать время истечения жидкости t, конечную высоту уровня воды h 2 в сосуде и объем вытекшей воды V.
5. Все измеренные величины занести в таблицу экспериментальных данных.
6. Повторить опыт пять раз.
7. Измерить и записать температуру в комнате и атмосферное давление.
8. Вычислить D P по формуле (16).
9. Найти для каждого опыта среднюю длину свободного пробега и эффективный диаметр молекул воздуха по формулам (15) и (18).
10. Вычислить средние значения длины свободного пробега <l> и эффективного диаметра d молекул воздуха и рассчитать случайные погрешности Dl и D d. Вычисленные величины занести в таблицу экспериментальных данных.
11. Записать окончательный результат в виде:
l = <l> ± Dl (м).
d = < d > ± D d (м).
12. Сравнить полученные значения величин l и d с литературными данными и сделать выводы по работе.
Таблица
Результаты измерений и вычислений
| № п/п | t (c) | V (м3) | h 1 (м) | h 2 (м) | Т к (К) | Р (Па) | D Р (Па) | l (м) | d (м) |
| Среднее значение | |||||||||
| Случайная погрешность |
Примечание: R = 8,314 Дж/моль×К;
М возд = 28,96×10–3 кг/моль;
n 0 = 2,69×1025 м–3;
1 мм рт. ст. = 133,3 Па.
Радиус r и длина l капилляра указаны на установке.
Контрольные вопросы
1. Что такое средняя длина свободного пробега молекулы?
2. От каких факторов зависит средняя длина свободного пробега молекулы?
3. На чем основано определение средней дины свободного пробега в данной работе?
4. Каков физический смысл эффективного диаметра молекул?
5. Явления переноса: теплопроводность, диффузия, вязкость. В чем суть явлений?
6. Какова связь между коэффициентами теплопроводности, диффузии и вязкости.
7. Какое явление описывает закон Пуазейля?
Литература:
Савельев И.В. Курс общей физики. Учеб. Пособие. В 3-х т. Т.1. Механика. Молекулярная физика. – 3-е изд., испр. – М.: Наука. Гл. ред. физ. мат. лит. 1986. 432 с.
