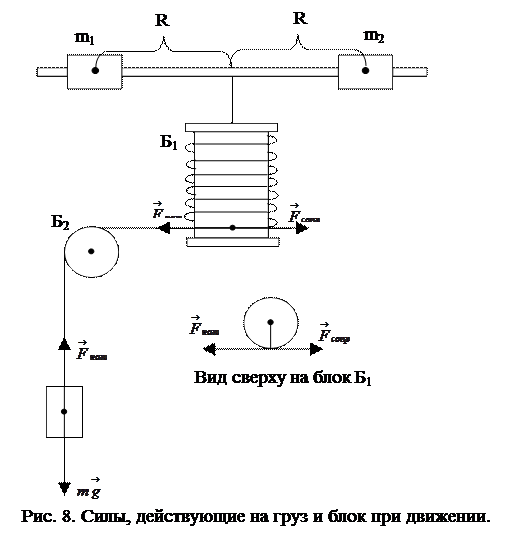
Описание установки. На вертикальной оси OO’ прибора жестко закреплен блок Б1 (см. рис 7), который можно привести в движение (вращение) с помощью намотанного на него шнура и груза m. На этой же оси закреплен стержень с массивными грузами m 1 и m 2, положение которых относительно оси можно изменять по желанию. Второй блок Б2, расположенный горизонтально, служит для изменения направления действующей силы. Путь H1, пройденный грузом m, можно измерять с помощью вертикальной шкалы. Установка снабжена тормозом Т. Описанное устройство называется инерционным маятником. Его параметры имеют следующие значения: m1=m2=(0.431±0.001)кг; P=mg=(1.506±0.005) H; lст=(0.510±0.005)м; mст=(0.111± 0.001) кг; r=(10-2± 5·10-5) м.
Описание эксперимента. Экспериментальная проверка основного закона динамики для вращающегося тела заключается в том, чтобы из экспериментальных данных определить независимо друг от друга величины M, I и i и сравнить полученное значение момента силы M со значением произведения I · i.
1. Определение углового ускорения вращающегося стрежня
с грузами
Пусть груз m опускается с высоты H1, ускоренно раскручивая при этом стержень с грузами. Угловое ускорение стержня можно определить из формулы, связывающей угловое и линейное ускорения:
, (1)
где a — линейное ускорение, с которым падает груз m и, следовательно, движется любая точка нити, сматывающейся с блока Б1; r — радиус блока Б1.
Линейное ускорение a можно найти из уравнения
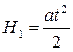, (2)
где H1 — высота, на которую опустился груз m за время падения; t — время падения груза. Из этой формулы получаем:
, (3)
Подставляя (3) в (1), получаем формулу для расчета углового ускорения:
, (4)
2. Определение момента инерции стержня с грузами
Момент инерции стержня с грузами складывается из момента инерции грузов m 1 и m 2 и момента инерции стержня:
. (5)
Моментом инерции легких блоков Б1 и Б2, ввиду их малости, можно пренебречь.
3. Определение момента силы, вызывающей раскручивание
стержня с грузами
На груз m при падении действуют две силы (см. рис. 8) — сила тяжести 
и сила натяжения нити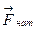 
. Под действием этих сил груз движется с ускорением a, существенно меньшим ускорения свободного падения:
На блок Б1 действуют силы натяжения нити 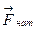и сопротивления 
. Их равнодействующая равна 
. Так как радиус блока является плечом силы, момент силы, вызывающей раскручивание, равен:
Можно принять 
, так как ускорение a мало.
Сила сопротивления находится на основании закона сохранения энергии. Падая с высоты H1, груз, после достижения наинизшего положения, поднимается на высоту H2. Часть потенциальной энергии mg (H1 - H2) переходит при этом в работу против сил сопротивления при раскручивании и закручивании нити на блок Б1:
Отсюда
,
Тогда
и
(6)
Определив M, I и i, можно сравнить величину момента силы M с величиной произведения I · i.
Рекомендуется проводить эксперименты при максимально возможной высоте падения груза H1 и при двух расстояниях от центров грузов m 1 и m 2 до оси вращения (R 1 = 20 см и R 2 = 10 см).
Порядок выполнения работы
1. Поставить грузы m 1 и m 2 так, чтобы расстояние от их центров до оси вращения было равно 20 см. Грузы должны быть надежно закреплены с помощью винтов. Измерить высоту падения (H1) груза m.
2. Установить верхний край груза m напротив деления 0 на шкале.
3. Открыть тормоз, одновременно включив секундомер.
4. Измерить время падения груза t, выключив секундомер в тот момент, когда груз опустится на всю длину нити.
5. Отметить деление шкалы, напротив которого остановится верхний край груза m при его подъеме вверх. Вычитая номер этого деления из H1, найти высоту H2, на которую поднялся груз m.
6. Опыт повторить пять раз при расстоянии до оси вращения R 1 = 20 см и еще пять раз — при R 1 = 10 см. Полученные результаты для H1, t и H2 занести в таблицу 1. Вычислить приближенные значения величин и абсолютные погрешности.
7. Вычислить величины i, I и M для R 1 = 20 см и R 1 = 10 см по формулам (4), (5), (6) соответственно, используя приближенные значения величин из таблицы 1. Полученные результаты занести в таблицу 2. Все расчеты проводить в системе СИ с точностью до трех значащих цифр.
8. Найти абсолютные и относительные погрешности для M и произведения (I · i) по формулам:
,
где
;
,
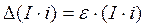где
,
принимая ΔI = 0,001 кг∙м2; ΔH1=ΔH2=5·10-3 м; ΔP=5·10-3 Н; Δr=5·10-5 м.
Расчеты провести один раз для случая R 1 или R 2.
9. Записать окончательный результат в виде:
Моп = М + ΔМ
(I∙i)оп = I∙i ± Δ (I∙i)
10. Сравнить доверительные интервалы, в которых лежат M и I · i, отложив эти интервалы на числовой оси. Если доверительные интервалы перекрываются, т.е. разность значений M и I · i по абсолютной величине меньше полусуммы доверительных интервалов, значения M и I · i совпадают в пределах погрешностей и закон подтверждается.
Таблица 1
Результаты измерений
| № п/п | H1 | R 1 = 0,2 м | R 2 = 0,1 м | ||
| t, с | H2, м | t, с | H2, м | ||
| Приближенное значение | |||||
| Абсолютная погрешность |
Таблица 2
Результаты вычислений
| i | I | I · i | M | |
| R 1 = 20 см | ||||
| R 2= 10 см |
