Чтобы проиллюстрировать возможности трех разобранных нами методов численного интегрирования, а также сравнить их точность, рассмотрим следующий интеграл:
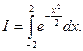
Для начала воспользуемся методом трапеций с довольно широким интервалом h= 1.0. При этом
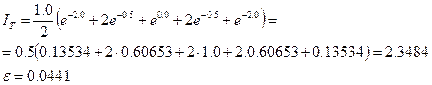
Метод Симпсона при h = 1.0 дает
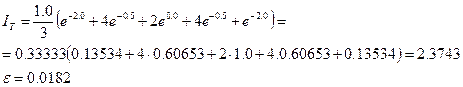
При использовании метода Гаусса с двумя ординатами приходится вычислять следующее выражение:
где:
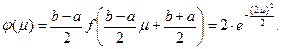
Подставляя численные значения, получаем
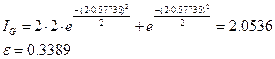
Повторяя эти же вычисления при h = 0.5 и при h = 0.25, а также при трех, четырех, пяти и шести точках в методе Гаусса, получаем результаты, приведенные в табл. 1.
Таблица 1
| Правило трапеций | h | IT | Ε |
| 1,0 | 2,3484 | 0,0441 | |
| 0,5 | 2,3813 | 0,0112 | |
| 0,25 | 2,3898 | 0,0027 | |
| Правило Симпсона | h | IS | Ε |
| 1,0 | 2,3743 | 0,0182 | |
| 0,5 | 2,3923 | 0,0002 | |
| 0,25 | 2,3926 | 0,0001 | |
| Метод Гаусса | Число точек | IG | Ε |
| 2,0536 | 0,3389 | ||
| 2,4471 | —0,0546 | ||
| 2,3859 | 0,0066 | ||
| 2,3931 | —0,0006 | ||
| 2,3925 | 0,0000 |
Конечно, нельзя выводить сколько-нибудь общие заключения из рассмотрения одного простого примера, но оказывается, что нижеследующие выводы имеют довольно общий характер.
1. Формула Симпсона при n ординатах дает примерно ту же степень точности, что и формула трапеций при 2n ординатах.
2. Метод Гаусса при n ординатах дает примерно ту же степень точности, что и формула Симпсона при 2п ординатах.
Хотя ни одно из этих утверждений не является совершенно точным, все же можно показать, что они приблизительно справедливы.
3. Для достижения той же степени точности при использовании формулы Симпсона приходится производить примерно вдвое меньше вычислений, чем по формуле трапеций, которая требует вдвое большего количества ординат.
4. Для достижения той же степени точности при использовании метода Гаусса приходится производить примерно вдвое меньше вычислений, чем по формуле Симпсона благодаря вдвое меньшему количеству ординат.
При «ручных» вычислениях метод Гаусса несколько неудобен тем, что абсциссы заданы заранее и выражаются, как правило, такими числами, с которыми очень неудобно работать. Например, гораздо легче искать по таблицам e-0.5, нежели e-0.16667. Однако при использовании ЭЦВМ эти соображения не играют никакой роли.
Экономия времени при использовании метода Гаусса имеет свою оборотную сторону. Дело в том, что если приходится заново вычислять тот же интеграл с большим количеством точек, то нельзя использовать ранее вычисленные ординаты, так как они находятся в неподходящих местах. В случае формулы Симпсона ранее вычисленные ординаты можно использовать снова (см. упражнение 14).
Для интегрирования при экспериментальных данных метод Гаусса можно использовать только тогда, когда абсциссы заранее правильно расположены; это случается очень редко. Формулой Симпсона можно пользоваться при условии, что интервалы разбиения одинаковы. Если же интервалы разбиения случайны, то для интегрирования можно применить лишь формулу трапеций. Формула Симпсона обеспечивает достаточную точность при умеренном количестве ординат, проста и удобна, так как позволяет легко измельчать разбиение интервала и заново вычислять интеграл. Поэтому неудивительно, что она получила широкое распространение в практических вычислениях.
9 ПРАКТИЧЕСКИЙ ПРИМЕР 8: СВЕТИМОСТЬ ЭЛЕКТРИЧЕСКОЙ ЛАМПОЧКИ
В этом практическом примере будут использованы описанные методы численного интегрирования, а также проиллюстрированы некоторые полезные приемы программирования.
Абсолютно черное тело (идеальный излучатель) излучает энергию пропорционально четвертой степени абсолютной температуры. Этот процесс описывается уравнением Стефана — Больцмана
где
Е —мощность излучения вт/см2,
Т — температура в градусах Кельвина. Нас интересует та часть общей энергии, которая заключена в видимом спектре частот. Здесь мы предположим, что видимый спектр соответствует длинам волн от 4*10-5 до 7*10-5 см. Эту часть энергии можно найти, интегрируя между вышеуказанными пределами уравнение Планка
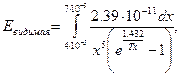
где х — длина волны в см.
Е и Т означают то же, что и в предыдущей формуле.
Светимостью мы назовем отношение энергии, заключенной в видимом спектре, к общей энергии излучения. Если умножить это отношение на 100, чтобы получить окончательный результат в процентах и перемножить коэффициенты, то задача сведется к вычислению интеграла
Необходимо написать программу, с помощью которой можно было бы вычислить EFF для некоторой последовательности температур, начиная с начальной температуры TEMPI до конечной ТЕМР2 с шагом TMPINC. С перфокарт необходимо также считывать границы видимого спектра A и B, чтобы эти величины тоже можно было при желании варьировать. Число отрезков разбиения при интегрировании задается с помощью целой переменной N, значение которой также следует прочитать с перфокарты. Ниже мы вернемся к вопросу о том, как велико должно быть N для достижения достаточной точности.
Блок-схема программы изображена на рис. 6. Работа программы начинается с ввода шести исходных значений, после чего производятся два действия, которые в дальнейшем не повторяются: вычисляется H - интервал разбиения, а переменной Т присваивается исходное значение ТЕМП1. После этого начинается собственно интегрирование. В программе предусмотрено вычисление двух сумм при интегрировании. Первая из них, обозначаемая SUM4, представляет собой сумму тех ординат, перед которыми в формуле Симпсона стоит коэффициент 4; вторая, обозначаемая SUM2, является суммой ординате коэффициентом 2. Поскольку по ходу программы потребуется вычислять значение подынтегральной функции в первой внутренней точке X + Н (это значение будет прибавлено к SUM4) и во второй внутренней точке (это значение будет прибавлено к SUM2), то переменной X присваивается соответствующее начальное значение.
Теперь мы сталкиваемся с некоторой трудностью. Для вычисления сумм необходимо пройти все внутренние значения X и затем остановиться. Если определять окончание цикла, сравнивая X и В — Н, т. е. проверять, находится ли X внутри интервала интегрирования, то возникают два неприятных обстоятельства. Во-первых, в формуле Симпсона количество ординат с коэффициентом 4 на единицу больше, нежели с коэффициентом 2. Поэтому нам придется остановиться, не доходя до конца интервала интегрирования, и прибавить к сумме значение ординаты в последней внутренней точке уже после окончания цикла. Во-вторых, если присвоить X исходное значение A + H и многократно прибавлять по 2Н, то ошибки округления будут накапливаться и в общем случае нам не удастся получить точное равенство X и B — 3Н.
Одно из возможных решений заключается в подсчете количества пройденных внутренних точек с помощью целой переменной I. Перед началом цикла интегрирования переменной I присваивается значение 1. (Легко определить значение I, при достижении которого следует выйти из цикла.) Таким образом, мы вычисляем подынтегральную функцию для двух очередных внутренних точек, прибавляем эти значения к соответствующим суммам и проверяем, не пора ли окончить цикл. Если нет, то мы увеличиваем
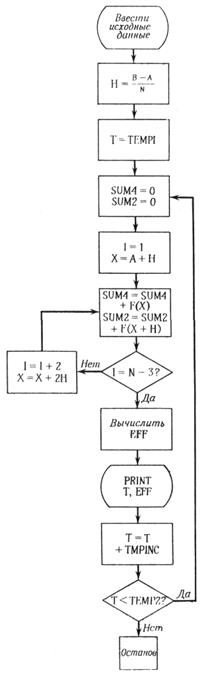
Рис. 6. Блок-схема программы для вычисления светимости. Интегрирование производится по формуле Симпсона (практический пример 8).
I и X и повторяем вычисления для следующей пары внутренних точек. Если цикл окончился, то необходимо перейти к вычислению EFF. В момент окончания цикла значение переменной SUM 4 равно сумме всех значений ординат, которые необходимо умножить на 4, за исключением ординаты в точке В — Н, которая должна быть вычислена дополнительно. Значение переменной SUM 2 равно сумме всех значений ординат, которые необходимо умножить на 2. Кроме того, остается добавить значения ординат в точках А и В. Таким образом, вычисление величины EFF производится с помощью длинного арифметического оператора, где вычисляются ординаты для А, В и В — Н, производятся умножения на 4 и на 2, а также на величину Н/3 и на 64.77/Т4.
После печатания результатов Т увеличивается на величину TEMPING и сравнивается с TEMP 2. Если новое значение не превосходит TEMP 2, т. е. если вычисления произведены еще не для всех температур, то мы снова переходим к вычислению интеграла. Если же светимость уже вычислена для наивысшей из заданных температур, то вычисления нужно прекратить.
Сама программа приведена на рис. 7. Предоставляем читателям самим внимательно прочесть ее, чтобы убедиться, что она в самом деле производит вычисления, графически изображенные на блок-схеме.
Рис. 6.7. Программа для вычисления светимости. Интегрирование производится по формуле Симпсона (практический пример 8).
Ошибку ограничения можно было бы оценить по ее верхней границе (см. разд. 6), но практически это вычисление требует гораздо больше труда, чем стоит затрачивать в данном случае. Во-первых, нужно было бы найти четвертую производную от
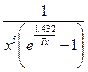
что само по себе является довольно трудоемкой задачей, хотя и вполне осуществимо. 3aтем нужно было бы каким-нибудь образом определить, где эта четвертая производная имеет максимум.
Гораздо удобнее воспользоваться помощью самой ЭЦВМ. Аналогично (18) в случае правила трапеций, следующая формула описывает экстраполяционный переход к пределу для формулы Симпсона
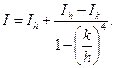
Это означает, что если, например, вычислить интеграл сначала при N = 10, а затем при N = 20, то можно оценить истинное значение интеграла. Кроме того, из величины разности между двумя значениями интеграла можно решить, каково должно быть N для достижения приемлемой точности результата.
Такие вычисления были проделаны по этой программе для Т = 3500° К. При 10 отрезках, вычисленное значение светимости было равно 14.512723%, а при 20 отрезках — 14.512664%. Разница двух значений настолько мала, что мы немедленно прекращаем дальнейшую погоню за точностью.
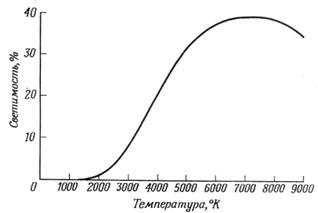
Рис. 6.8. Зависимость светимости от температуры (°К) для черного тела (практический пример 8).
Наконец, хотя это уже и не имеет прямого отношения к численному анализу, интересно построить график зависимости светимости от температуры, как показано на рис. 6.8. Из графика следует, что видимая часть общей энергии пренебрежимо мала при температурах, меньших 2000° C, что при температуре плавления вольфрама (3600° К) только около 15% общей энергии излучения находится в видимой области спектра и что кривая имеет широкий максимум около 7000° К. Соображения этого рода определяют верхний предел коэффициента полезного действия осветительных ламп накаливания. Интересно было бы также сделать некоторые предположения, относящиеся, например, к стоимости электроэнергии, времени жизни нити накаливания в зависимости от температуры и стоимости лампочки, и вычислить температуру, при которой «полная стоимость» света, включая электроэнергию и лампочку, была бы минимальной.
Упражнения
1. Вычислите точное значение интеграла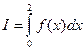 
, а также приближенные значения по формуле трапеций при h = 1.0 и по формуле Симпсона с h = 1.0. В качестве f(x) возьмите следующие функции:
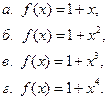
2. Дайте доказательство и геометрическое истолкование следующего факта: если в интервале а<=x<=b f"(x)>0, то приближенное значение интеграла 
, вычисленное по формуле трапеций, будет всегда больше, нежели его точное значение. (Говорят, что подобные функции f(x) направлены выпуклостью книзу.)
3. Рассмотрим интеграл 
. Покажите, что формула Симпсона с h = 1 и метод Гаусса с двумя ординатами позволяют вычислить точное значение интеграла, хотя при использовании метода Гаусса требуется одной ординатой меньше по сравнению с формулой Симпсона.
4. Рассмотрим интеграл 
. Покажите, что приближенное значение, вычисленное по формуле Симпсона при h = 0.5, поразительно близко к истинному значению (с точностью примерно 1/3000). Объясните «качественно», почему получается такое близкое совпадение.
5. В противоположность упражнению 4, рассмотрим часто встречающийся интеграл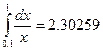 
. Ниже приведены приближенные значения интеграла, вычисленные по формуле Симпсона при трех различных разбиениях, а также ошибки для каждого случая. Объясните разницу между результатами этого и предыдущего упражнения.
| N | h | IS | Ошибка |
| 0.45 | 3.3500 | -1.0474 | |
| 0.225 | 2.4079 | -0.1053 | |
| 0.1125 | 2.3206 | -0.0180 |
6. Примените экстраполяционный перевод к пределу, чтобы найти лучшее приближение к точному значению интеграла 
. Используйте две последние строки предыдущей таблицы. По виду уравнения (18) можно было бы предположить, что окончательный результат будет точным. Почему это не так?
7. Полный эллиптический интеграл первого рода определяется формулой
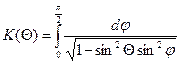
Вычислите K(30°), воспользовавшись формулой Симпсона с четырьмя отрезками. Точный результат до четвертого знака после запятой равен 1.6858. Вычислите также К(85°), снова воспользовавшись формулой Симпсона с четырьмя отрезками. На этот раз точный результат до третьего знака после запятой равен 3.832. Почему К(85°) получилось с такой большой ошибкой, в то время как К(30°) было вычислено довольно точно?
8. Рассмотрим следующий интеграл[4]
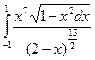
Напишите программу для вычисления этого интеграла по формуле Симпсона. Программу составьте так, чтобы значение шага разбиения h можно было вводить с перфокарты. Вычислите значение интеграла при h=0.25, затем 0.1, 0.05, 0.02 и 0.01. Объясните несколько неожиданное поведение окончательного результата при уменьшении h. (Заметим, что объяснить поведение окончательного результата, возможно, будет легче, если предусмотреть в программе печать ординат функции.)
9.* Рассмотрим интеграл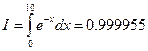 
Вычислите этот интеграл с помощью:
а. Метода Гаусса с 6 точками;
б. Правила трапеций с 10 отрезками;
в. Правила Симпсона с 10 отрезками;
г. Правила прямоугольников из упражнения 18 с 10 отрезками. Сравните результаты вычислений. В какую сторону лучше двигаться при интегрировании: от 0 к 10 или от 10 к 0? Почему?
10.* Напишите программу вычислений из упражнения 9.
11. Обобщите программу из упражнения 10 для формулы Симпсона так, чтобы в нее можно было ввести значения a, b и n и вычислить требуемое значение h.
12. К программе из упражнения 11 добавьте проверку, является ли n четным. При нечетном n вычисление интеграла производить не следует. (Указание: при делении целых чисел дробная часть результата отбрасывается; если N является нечетным, то (N/2)*2 не равно N.)
13. Усовершенствуйте программу, приведенную на рис. 7, так, чтобы при ее работе вычислялись и печатались значения светимости, полученные по формуле трапеций и по формуле Симпсона. Ординаты должны быть вычислены только один раз.
14. Предположите, что вычисления по программе, приведенной на рис. 7, уже закончены и теперь необходимо вычислить тот же интеграл, но для вдвое более мелкого разбиения. Все ординаты, рассчитанные ранее и просуммированные в ячейках SUM4 и SUM2, понадобятся при новом вычислении интеграла, так как это как раз те ординаты, сумму которых необходимо умножить на 2. Кроме того, придется рассчитать ординаты в центрах каждого из отрезков предыдущего разбиения. Видоизмените программу таким образом, чтобы после вычисления интеграла с разбиением, определяемым величинами А, В и N, те же расчеты повторились с удвоенным количеством точек; при этом ни одна ордината не должна вычисляться дважды. Имея два приближенных значения интеграла, используйте экстраполяционный переход к пределу, чтобы получить еще более точное значение.
15. Напишите программу, которая предусматривала бы ввод значений a0, a1, a2, a3, a4, a5 и a6 и значений a, b и n, вычисление и печать значения интеграла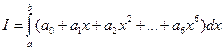 
. Для вычислений используйте метод Симпсона с n отрезками.
16. Видоизмените программу, приведенную на рис. 7, предусмотрев в ней определение максимума светимости, если он, максимум, попадает в заданную для вычислений область температур. Если существуют такие три последовательных значения температуры, что EFF (T1) < EFF (T2) > EFF (T3), то необходимо их напечатать вместе с соответствующими светимостями. Если три таких значения найти не удается, то вместо всех этих шести величин необходимо напечатать нули.
17. Предположите, что заданы три значения x = -h, 0 и h и три соответствующих значения у = у0, y1 и y2. Подставьте эти три пары значений в общее уравнение параболы у=а+bх+сх2 и решите три получившихся уравнения относительно а, b и с. Используя вычисленные таким образом a, b и c, проинтегрируйте уравнение параболы в пределах от — h до h и покажите, что результат будет равен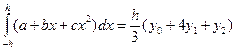 
Таким способом обычно выводится формула Симпсона для численного интегрирования в учебниках по математическому анализу.
18. Выведите формулу численного интегрирования для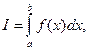 
разделив интервал интегрирования на n равных отрезков длиной 
. В качестве приближенного значения площади для каждого интервала примите площадь прямоугольника, высота которого равна значению f(x) на левом краю интервала (см. схему).
19. Покажите, что ошибка ограничения для формулы, выведенной в упражнении 18, равна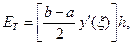 
где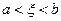 
.
20. Примените экстраполяционный переход к пределу, чтобы с помощью формулы численного интегрирования, выведенной в упражнении 18, и формулы ошибки ограничения, выведенной в упражнении 19, получить новую формулу численного интегрирования.
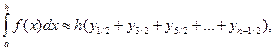
где
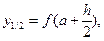
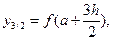
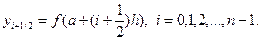
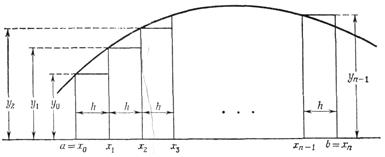
Объясните формулу геометрически.
21. Ошибка ограничения при численном интегрировании по формуле из упражнения 20 равна
Сравните ее с ошибкой ограничения при интегрировании по формуле трапеций. Объясните, почему эти ошибки имеют одинаковый порядок.
22. Покажите, что формула численного интегрирования по методу Гаусса, которая дает точный результат только для линейной функции, имеет следующий вид:
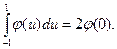
23. Предположим, что при интегрировании с помощью метода трапеций n=3m, т. е. количество отрезков разбиения кратно 3. Напишите формулы численного интегрирования по формуле трапеций для случая, когда длина отрезка разбиения равна A, и для случая, когда она равна k=3h. Используйте экстраполяционный переход к пределу и выведите новую формулу численного интегрирования
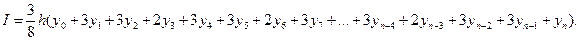
Эта формула иногда называется правилом трех восьмых. Ее можно было бы вывести, приближая интеграл от исходной функции на трех соседних отрезках интегралом от кубической параболы, проведенной через четыре последовательные ординаты.
Ошибка ограничения для этой формулы имеет вид
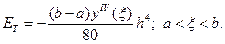
Сравните ее с ошибкой ограничения при интегрировании по правилу Симпсона. Обладает ли формула трех восьмых какими-нибудь преимуществами перед формулой Симпсона?
24. Предположим, что при интегрировании по формуле Симпсона n = 4m. Напишите формулы численного интегрирования по правилу Симпсона для случаев, когда величина отрезка разбиения равна h и k = 2h. Используйте экстраполяционный переход к пределу для вывода формулы
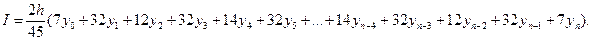
Это четвертая формула Ньютона—Котеса (первыми тремя являются формула трапеций, формула Симпсона и формула трех восьмых). Соответствующая ошибка ограничения записывается в виде
25. Рассмотрим несобственный интеграл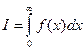 
, где f(x) представляется в виде 
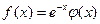. Покажите, что если φ(x) является многочленом степени не выше 3, то I можно точно вычислить по формуле 
где
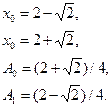
Это формула Лагерра—Гаусса второго порядка. Названием своим она обязана тому факту, что х0 и x1 являются корнями полинома Лагерра второго порядка.
Читателям, интересующимся общим выводом и таблицами абсцисс и весовых коэффициентов для формул Лагерра—Гаусса более высоких порядков, рекомендуем книги Гильдебранда (разд. 6).
26. Покажите, что если f(x) является многочленом степени не выше 3, то
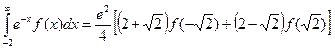
(Указание: заменой переменных сведите задачу к виду, рассмотренному в упр. 25)
27. Рассмотрим несобственный интеграл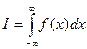 
, где f(x) представляется в виде 
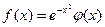. Покажите, что если φ(х) является многочленом степени не выше 3, то точное значение интеграла можно вычислить по формуле 
.
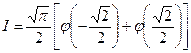Это формула Эрмита — Гаусса второго порядка. Своим названием она обязана тому факту, что абсциссы, где вычисляется φ, являются корнями полинома Эрмита второго порядка. Более подробные сведения можно найти в книгах Гильдебранда.
Указание: вспомните, что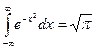 
.
28. Используйте дважды метод трапеций и выведите формулу
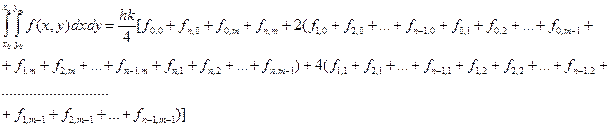
где
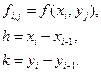
С помощью этой формулы можно производить вычисление двойных интегралов в прямоугольной области. Можно получить и другие формулы для вычисления двойных интегралов, применяя дважды соответствующие правила численного интегрирования (например, правило Симпсона).
29*. Инженер желает получить «наилучший» средний отсчет измерительного прибора на протяжении часа. Через сколько минут после начала измерений необходимо снимать показания прибора, если
на протяжении часа можно снять два отсчета;
на протяжении часа можно снять три отсчета;
на протяжении часа можно снять четыре отсчета.
Ответ следует округлить до ближайшего целого.
30. Предположим, что имеются экспериментальные результаты, согласно которым y является некоторой (неизвестной) функцией от x.
| x | y | x | y |
| 1.0 | 1.00 | 2.2 | 5.12 |
| 1.2 | 1.82 | 2.4 | 6.38 |
| 1.4 | 2.08 | 2.6 | 6.98 |
| 1.6 | 3.18 | 2.8 | 8.22 |
| 1.8 | 3.52 | 3.0 | 9.00 |
| 2.0 | 4.70 |
Вычислите приближенное значение интеграла 
, воспользовавшись следующими методами:
а. Правилом трапеций,
б. Формулой Симпсона,
в. Правилом трапеций для интервалов от 1.0 до 1.2 и от 2.8 до 3.0 и формулой Симпсона для интервала от 1.2 до 2.8.
Если о характере зависимости у от x больше ничего неизвестно, можно ли сказать, какой результат является «наиболее точным»? 31. Имеются некоторые экспериментальные данные, согласно которым y является некоторой (неизвестной) функцией от х.
| x | y | X | Y |
| 0.21 | 0.43 | ||
| 0.30 | 0.37 | ||
| 0.37 | 0.33 | ||
| 0.45 | 0.29 | ||
| 0.49 | 0.25 | ||
| 0.50 | 0.19 | ||
| 0.49 | 0.13 | ||
| 0.47 | 0.08 | ||
| 0.45 | 0.04 |
Вычислите приближенное значение интеграла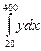 
, воспользовавшись формулой трапеции.
[1] Интересующимся читателям рекомендуются книги Alt F., Electronic digital computers, Academic Press, New York, 1958, p. 203—205; Коpa1 Z., Numerical Analysis, Wiley, New York, 1961, p. 370—386.
[2] Richardson L. F.,Gaunt J. A., The deferred approach to the limit, Trans. Roy. Soc. London, 226 A, 300 (1927).
[3] См., гл. 3 книги Гильдебранда: Нildebгаnd F. В., Introduction to numerical analysis, McGraw-Hill, 1956
[4] Scarborough J. В., Numerical mathematical analysis, The Johns Hopkins Press, 1950.
