Экстраполяционный переход к пределу

 

Чтобы найти более точное значение интеграла, можно воспользоваться сравнительно простым усовершенствовани­ем метода трапеций.

Вспомним (см. формулу (14)), что для шага h ошибка ограничения составляет е_T=Ch²

где

Если вторую производную от у считать постоянной, то C также является константой.

Предположим теперь, что выбрана некоторая другая величина шага разбиения , причем m ≠ n. Тогда е_T = Ck².

Теперь пусть I_h — значение интеграла, вычисленное по правилу трапеций с шагом h, а I_k — значение, вычислен­ное с шагом k. При этом

I = I_h + Сh² (16)

и

I = I_k + Ck².

Если вычесть эти два уравнения друг из друга, то можно определить С

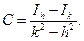(17)

Подставляя это значение C в (16), получаем

(18)

Вычисленное таким образом значение интеграла I являет­ся лучшим приближением, чем I_h или I_k. Если же вторая производная у" (х) действительно постоянна при a <= x <= b, то ошибка ограничения в формуле (18) равна нулю.

Этот метод называется экстраполяционным переходом к пределу; предложен он Ричардсоном[2].

 

ПРАВИЛО СИМПСОНА

 

В этом параграфе мы рассмотрим один из наиболее широко известных и применяемых методов численного интег­рирования, а именно правило Симпсона. Этот метод анало­гичен правилу трапеций в той части, что интегрирование производится путем разбиения общего интервала интегри­рования на множество более мелких отрезков; однако теперь для вычисления площади над каждым из них через три после­довательных ординаты разбиения проводится квадратич­ная парабола. Можно было бы ожидать, что аналогично тому, как правило трапеций дает точный результат при интегрировании линейных функций, правило Симпсона даст точный результат при интегрировании многочленов второ­го порядка; в действительности же получается несколько парадоксальный результат: формула Симпсона дает точные значения интеграла при интегрировании многочленов до третьего порядка включительно. Поэтому при всей своей простоте этот метод весьма точен, хотя формула для числен­ного интегрирования получается ненамного сложней, чем для правила трапеций. Простота и точность правила Симп­сона сильно способствуют его широкому применению при вычислениях на ЭЦВМ.

Вспомним, что количество отрезков n в случае правила трапеций определялось формулой .

Предположим теперь, что число n является четным и что

(19)

Тогда

(20)

(21)

Уравнения (19), (20) и (21) можно подставить в (18). При этом получим

И окончательно

(22)

Формула (22) называется формулой Симпсона. Ее можно было вывести другим путем, а именно проводя параболу через три ординаты на концах двух соседних интервалов и потом складывая получившиеся при этом площади. Читатели могут проделать эти выкладки самостоятельно и геометрически истолковать разницу между формулами интегрирования.

Ошибка ограничения при интегрировании с помощью формулы Симпсона может быть вычислена таким же способом, как и для правила трапеций в разд. 3. Не воспроизводя здесь выкладки, приведем окончательный результат:

Заметим, что ошибка пропорциональна h⁴, в то время как для метода трапеций ошибка была пропорциональна h². Это означает, что метод Симпсона соответствует ряду Тейлора в формуле (7) с точностью до членов третьего порядка включительно, а метод трапеций соответствует этому ряду только с точностью до членов первого порядка. Поэтому при интегрировании многочленов степени не выше третьей метод Симпсона дает точные значения интеграла (так как f^IV(х) = 0).

Если предположить, что четвертая производная практи­чески постоянна, то снова можно применить экстраполяционный переход к пределу и улучшить результаты интегриро­вания по методу Симпсона. Вообще говоря, подобно тому, как была выведена формула (22), можно повышать точ­ность, проводя через последовательные ординаты многочле­ны более высоких степеней. В результате получаются фор­мулы Ньютона-Котеса[3].

Наконец, опять без вывода, заметим, что верхняя грани­ца возможной ошибки округления при интегрировании по правилу Симпсона пропорциональна 1/h, как и для формулы трапеций.

На рис. 4 изображен также график зависимости общей ошибки от числа интервалов при интегрировании sin x от 0 до π по формуле Симпсона. На графике ясно видно, что при использовании формулы Симпсона ошибка уменьшается гораздо быстрее (h⁴ по сравнению с h²). Так как ошибки округления для обоих случаев примерно одинаковы, то при использовании формулы Симпсона ошибка округления начи­нает преобладать в общей ошибке гораздо раньше. Из рисунка видно, что общая ошибка возрастает при π > 50.

МЕТОД ГАУССА

 

В предыдущих параграфах рассматривались методы чис­ленного интегрирования с произвольным разбиением интер­вала. Фактически разбиение производилось на равные отрезки.

Зададимся теперь вопросом: нельзя ли уменьшить ошиб­ку ограничения при заданном количестве интервалов, если располагать концы интервалов там, где это требуется из условий достижения наивысшей точности интегрирова­ния? С философской точки зрения, следует ожидать улуч­шения: пожертвовав свободой при выборе разбиения интер­вала, мы вправе потребовать взамен увеличения точности. Оказывается, точность в самом деле увеличивается.

Вспомним, что рассмотренное ранее правило трапеций позволяло при двух ординатах найти точное значение интег­рала от линейной функции (многочлена первого порядка). Сейчас будет показано, что при соответствующем выборе местоположения двух ординат можно получить точный результат для многочлена третьего порядка. Интуитивно очевидно, что погрешность метода тем меньше, чем выше порядок многочлена, при численном интегрировании кото­рого получается точный результат. Мы не будем здесь дока­зывать этого во всей полноте.

Чтобы упростить выкладки, изменим пределы интегри­рования так, чтобы они стали равными (+1, -1). Для этого введем новую переменную

так что

Интеграл (1) после такой подстановки запишется в виде

(23)

где

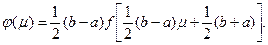
Это означает, что соответствующей заменой переменных можно свести все интегралы к виду (23). (Под «всеми» подразумеваются интегралы с конечными пределами интег­рирования и с непрерывной подынтегральной функцией.)

Попытаемся определить, чего можно добиться при нали­чии всего двух ординат, т. е. в том случае, когда кривая, которой мы заменяем подынтегральную функцию, является прямой линией. Другими словами, попытаемся найти такую линейную функцию

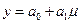
для которой

(24)

Рис. 5. Геометрическое представление метода Гаусса с двумя

ординатами.

 

Интеграл, стоящий в левой части этого уравнения, пред­ставляет собой площадь трапеции на рис. 5. Пусть сумма площадей вертикально заштрихованных участков (между -1 и μ₀ и от μ₁ до +1) равна площади зачерненного участ­ка (между μ₀ и μ₁). Тогда площадь трапеции в точности равна площади под кривой y=φ(μ). Задача заключается в нахождении такой прямой линии, для которой достигается это равенство.

Положим

(25)

где необходимо определить А₀, A₁, μ₀ и μ₁. Так как в форму­ле имеются четыре параметра, то естественно предположить,

что формула даст точный результат при интегрировании кубической параболы

Перепишем эту функцию в виде

Если a₀ и a₁ должны удовлетворять уравнению (24), то μ₀ и μ₁ определяется из условия

Так как это равенство должно быть справедливо для любых β₀ и β₁ то необходимо потребовать выполнения двух следующих равенств:

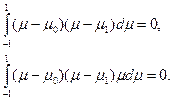
Выполнив интегрирование, можно записать два послед­них равенства в виде

откуда следует, что

(26)

Теперь остается только найти A₀ и A₁ в формуле (25). Заметим, что

(27)

и из формул (25) и (26) следует, что

Так как значение выражения в правой части последней формулы должно быть равно значению интеграла в формуле (27) при всех a₀ и а₁, то для А₀ и A₁ получаем систему уравнений

из которой находим

А₀ = A₁ = 1. (28)

Уравнение (25) окончательно запишется в виде

Это и есть формула численного интегрирования Гаусса для случая двух ординат. Ошибка ограничения равна нулю при интегрировании многочленов до третьего порядка вклю­чительно. Естественно ожидать, что при интегрировании многочленов высших степеней и прочих функций ошибка ограничения будет определяться формулой

где

(29)

Чтобы найти К, предположим, что При этом так что

(30)

Точное значение интеграла легко вычислить:

С другой стороны, из формул (29) и (30)

Поэтому K=1/135, и окончательная формула для ошибки ограничения запи­шется в следующем виде:

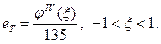
Можно вывести гауссовы формулы численного инте­грирования более высоких порядков, предусматривая большее количество ординат и вводя различные весовые коэффициенты А_i.

(31)

В общем случае, при (n + 1) ординате, получается точ­ная формула для нахождения интеграла от многочлена степени 2n + 1.

Оказывается, что значения μ_i в уравнении (31) являют­ся корнями полиномов Лежандра степени n. По этой причи­не вышеописанный метод численного интегрирования часто называют методом Лежандра — Гаусса. Полиномы Лежанд­ра P_n(μ) можно найти с помощью рекуррентных формул

(32)

Например, для m = 2

Заметим, что корни Р₂ (μ) равны , как мы уже опре­делили ранее.

Весовые коэффициенты в формуле (31) можно найти из следующего соотношения:

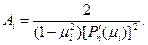
В качестве примера возьмем n = 2, так что μ ₀ = - , μ₁ = и Р’₂= 3μ. При этом

и совершенно аналогично A₁ = 1.

В общем случае ошибка ограничения определяется формулой

Таблица μ_i, и A_i для n = 2,...,6 приведена в приложе­нии. Заметим, что μ_i расположены симметрично относительно начала координат и что коэффициенты A_k одинаковы для μ_k и для — μ_k. Более подробная таблица вплоть до n = 48 приведена в приложении к книге В. И. Крылова «Прибли­женное вычисление интегралов».

Итак, метод Гаусса позволяет достичь большей точности, нежели формула Симпсона при том же количестве ординат, но зато точки, где следует определять эти ординаты, пол­ностью определены и совершенно не зависят от произвола программиста. Как и во многих других случаях, при чис­ленном интегрировании приходится делать выбор между простотой формулы Симпсона и возможной экономией машинного времени при использовании метода Гаусса. На практике чаще используется метод Симпсона.