Исследование функций и построение графиков с помощью производной
Теория: Кремер Н.Ш. «Высшая математика для экономистов» учебник с.217-242
Краткая информация о новых учебных элементах
1. Значение функции  в точке
в точке 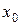 называется максимумом (минимумом), если оно является наибольшим (наименьшим) по сравнению с ее значениями во всех достаточно близких точках слева и справа от
называется максимумом (минимумом), если оно является наибольшим (наименьшим) по сравнению с ее значениями во всех достаточно близких точках слева и справа от 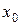 .
.
2. Функция может иметь экстремум (максимум или минимум) в тех точках, которые лежат внутри области определения функции и в которых производная равна 0. Такие точки называются критическими.
3. Функция будет иметь экстремум в тех точках, где ее производная меняет свой знак, а сама функция непрерывна.
4. Если в некотором интервале кривая расположена ниже любой своей касательной, то она называется выпуклой вверх, а если она расположена выше любой своей касательной, то называется выпуклой вниз в этом интервале.
5. Направление выпуклости кривой  характеризуется знаком второй производной
характеризуется знаком второй производной 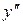 .
.
Если 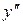 меняет свой знак при переходе через точку, в которой
меняет свой знак при переходе через точку, в которой  или не существует, то данная точка является точкой перегиба.
или не существует, то данная точка является точкой перегиба.
6. Асимптотой кривой называется такая прямая, к которой график функции неограниченно приближается. Если  , то прямая
, то прямая  называется асимптотой вертикальной. Если существует наклонная асимптота, то ее уравнение имеет вид:
называется асимптотой вертикальной. Если существует наклонная асимптота, то ее уравнение имеет вид:
 причем
причем  ,
,  .
.
Задача 1. Исследовать функцию  и построить ее график.
и построить ее график.
1. Область определения данной функции – все действительные числа, так как функция представляет собой многочлен.
2. Точки пересечения с осями.
Если точка лежит на оси Оу, то 
 .
.
Если точка лежит на оси Ох, то  .
.
Для решения кубического уравнения
а) рассмотрим делители свободного члена  :
:  ; если
; если 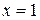 , то
, то  , значит
, значит  корень данного уравнения.
корень данного уравнения.
б) разделим многочлен  на двучлен
на двучлен  , т.е.
, т.е. 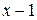 :
:

в) решим квадратное уравнение:
 .
.
Значит, график пересекает ось Ох в точке 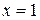 и касается в т.
и касается в т. 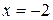 .
.
3. Промежутки знакопостоянства функции.
Итак, многочлен, определяющий данную функцию можно разложить на множители:  . Определим знак функции в каждом из интервалов:
. Определим знак функции в каждом из интервалов:

Если  , то
, то  .
.
Если  , то
, то  .
.
Если  , то
, то  .
.
Значит, на 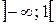 график функции располагается ниже оси Ох, а на
график функции располагается ниже оси Ох, а на 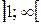 - выше.
- выше.
4. Чётность.
Вычислим  .
.
 и
и  .
.
Значит, функция не обладает данными свойствами.
5. Исследование на экстремум.
 ;
;
 критические точки.
критические точки.
Составим таблицу и определим знак производной в каждом интервале.

| 
| 
| 
| 
| 
| 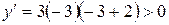
| |

| + | 
| + | 
| 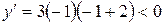
| ||

| 
| max | 
| min | 
| 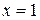
| 
|
Найдем значения функции в точках экстремума.
 ;
;
 .
.
Изобразим эти точки на графике.

Рис. 5
6. Исследование на перегиб.
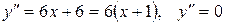 , если
, если  . При переходе через эту точку
. При переходе через эту точку 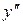 меняет знак, т.к.
меняет знак, т.к. 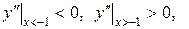
 .
.
Отметим эту точку  на графике.
на графике.
Подставим координаты  в уравнение
в уравнение  где
где  :
:
 ,
,
значит, касательная имеет уравнение  . Построим ее:
. Построим ее:
| х | 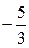
| |
| у | 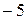
|
7. Построение графика (рис. 5).
Для уточнения положения графика найдем координаты некоторых его точек:
| х | 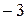
| 
|
| у | 
| 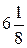
|
Задача 2. Исследовать функцию и построить ее график:
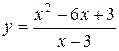 .
.
Решение. 1. Область определения функции.
Делить на 0 нельзя, поэтому  ,
,  , значит
, значит  вертикальная асимптота.
вертикальная асимптота.
2. Точки пересечения с осями.
С осью Оу:  ,
, 
 ;
;
С осью Ох: 
 .
.
3. Промежутки знакопостоянства функции:
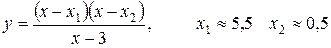

 при
при 
 при
при 
 при
при 
 при
при 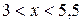 .
.
4. Исследование на экстремум.
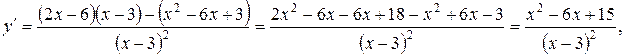
 .
.
Экстремума нет, т.к. критическая точка  , в которой
, в которой  , не входит в область определения.
, не входит в область определения.
5. Исследование на перегиб.

 .
.
При переходе через точку  кривая меняет направление выпуклости, но т.к. эта точка является точкой разрыва, значит «перегиба» не существует.
кривая меняет направление выпуклости, но т.к. эта точка является точкой разрыва, значит «перегиба» не существует.

Рис. 6
6. Построение асимптот (наклонных):  .
.


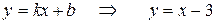 .
.
Строим прямую по точкам:
| х | ||
| у | 
|
7. Построение графика (рис. 6).
Для уточнения положения графика найдем значение заданной функции в точках 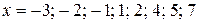 .
.
| х | 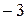
| 
| 
| |||||
| у | 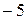
| 
| 
| 
| 
| 2,5 |




Задача 3. Исследовать функцию и построить ее график:
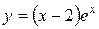 .
.
1. Область определения – все действительные числа.
2. Точки пересечения с осями.
С осью Оу: 
С осью Ох:  .
.
3. Промежутки знакопостоянства функции.

 ;
;
 .
.
4. Исследование на экстремум.
 ;
;
 .
.
| х | 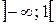
| 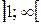
| |

| 
| 
| 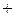
|
| у | 
| min | 
|
 .
.
5. Исследование на перегиб.
 .
.
 - точка перегиба, т.к.
- точка перегиба, т.к.  при всех х.
при всех х.
 при
при 
 при
при 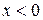 .
.
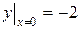 . Точка перегиба
. Точка перегиба 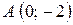 .
.
6. Построение асимптот.
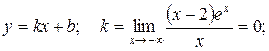
 .
.
Следовательно, ось Ох является горизонтальной асимптотой.
7. Для построения графика (рис. 7) вычислим значения функции в некоторых точках:
 ;
; 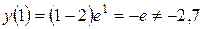 .
.

Рис. 7






