I. Обозначения
1. P — цена
2. Q — количество
3. D – спрос
4. S — предложение
5. QD – величина спроса
6. QS – величина предложения
7. Qдеф – дефицит (объем дефицита)
8. Qпродаж – объём продаж
9. QИЗБ – объём избытка (излишки)
10. EDP– коэффициент эластичности спроса по цене
11. ESP– коэффициент эластичности предложения по цене
12. I – доход
13. EDI- коэффициент эластичности спроса по доходу
14. EDC- коэффициент перекрестной эластичности спроса
15. TR – совокупный доход (выручка продавца)
16. TC – общие затраты
17. Pr – прибыль
18. PD – цена спроса
19. PS– цена предложения
20. PE– равновесная цена
II. Формулы:
1. y= k*x+b – уравнение описывающее функцию спроса
2. QD= k*P+b – функция спроса
3. EDP= Δ QD (%)/ΔP (%) – коэффициент эластичности спроса по цене
4. EDP= (Q2 –Q1): (Q2 + Q1)/ (P2 –P1): (P2 + P1) – формула средней точки, где P1 – цена товара до изменения, P2 – цена товара после изменения, Q1 – величина спроса до изменения цены, Q2 – величина спроса после изменения цены;
5. EDI= (Q2 –Q1): (Q2 + Q1)/ (I2 –I1): (I2 + I1) – формула коэффициента эластичности спроса, где I1 – величина дохода до изменения, I2 – величина дохода после изменения, Q1 – величина спроса до изменения дохода, Q2 – величина спроса после изменения дохода;
6. EDС = (Q2 –Q1): (Q2 + Q1)/ (P2 –P1): (P2 + P1) – формула средней точки, где P1 – цена второго товара до изменения, P2 – цена второго товара после изменения, Q1 – величина спроса первого товара до изменения цены, Q2 – величина спроса первого товара после изменения цены;
7. TR = P*Q – формула расчета выручки продавца
8. Pr= TR – TС – формула расчета прибыли;
9. QD= k*P+b – функция предложения;
10. ESP= (QS2 –QS1): (QS2 + QS1)/ (P2 –P1): (P2 + P1) – формула коэффициента предложения, где P1 – цена товара до изменения, P2 – цена товара после изменения, QS1 – величина предложения до изменения цены, QS2 – величина предложения после изменения цены;
11. Qдеф = QD- QS – формула для определения объема дефицита;
12. Qдеф = QS — QD – формула для определения объема излиш
Формула расчёта необходимого для обращения количества денег:
1)
КД — масса денег;
Ецт — сумма цен товаров;
К — товары, проданные в кредит;
СП — срочные платежи;
ВП — взаимопогашаемые платежи (бартерные сделки);
СО — скорость оборота денежной единицы (в год).
2)
M — денежная масса, находящаяся в обращении;
V — скорость обращения денег;
Р — средние цены на товары и услуги;
Q — количество произведенной продукции в постоянных ценах.
Уравнение обмена:
M — денежная масса, находящаяся в обращении;
V — скорость обращения денег;
Р — средние цены на товары и услуги;
Q — количество произведенной продукции в постоянных ценах.
Это уравнение показывает, что совокупные расходы в денежном выражении
равны стоимости всех товаров и услуг, произведенных экономикой.
Формула для нахождения реального дохода:
ИПЦ - индекс потребительских цен.
Формула для нахождения покупательной способности денег:
Iпcд - покупательная способность денег;
Iц - индекс цен.
Формула для нахождения индекса потребительских цен:
Формула для расчёта стоимости потребительской корзины:
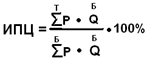
P 1 — цена первого товара;
Р 2 — цена второго товара;
Р n — цена n-го товара;
Q 1 — количество первого товара;
Q 2 — количество второго товара;
Q n — количество n-го товара.
Формула для расчёта темпа инфляции:
В зависимости от темпа инфляции различают несколько ее видов:
1.Мягкая (ползучая), когда цены растут в пределах 1—3% в год.
2.Умеренная — при росте цен до 10% в год.
3.Галопирующая — при росте цен от 20 до 200% в год.
4.Гиперинфляция, когда цены растут катастрофически — более чем 200% в год.
Формула для расчёта простого процента:
P - сумма долга с процентами;
S - сумма кредита;
n - число дней;
i - годовой процент в долях.
Формула для расчёта сложного процента:
P - сумма долга с процентами;
S - сумма кредита;
n - число дней;
i - годовой процент в долях;
N - сколько раз начисляется в году.
Формула для расчёта сложного процента начисляемого за несколько лет:
P - сумма долга с процентами;
S - сумма кредита;
t - число лет;
i - годовой процент в долях.
Формула для расчёта смешанного процента за дробное колличество лет:
P - сумма долга с процентами;
S - сумма кредита;
t - число лет;
i - годовой процент в долях;
n - число дней.
Формула для расчёта банковских резервов:
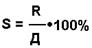
S - норма обязательных резервов в процентах;
R - общая сумма резервов;
Д - величина депозитов на счету КБ.
Формула расчёта уровня безработицы:
Формула расчёта уровня занятости:
Формула расчёта перекрёстной ценовой эластичности:
Формула расчёта концепции эластичности:
Формула расчёта амортизации:
1)
2)
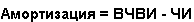
Формула расчёта личного дохода домохозяйств:
Формула расчёта ВНП по доходам:
Формула расчёта ВНП по расходам:
Формула расчёта ЧНП:
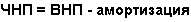
Формула расчёта средних общих издержек:
1)
2)
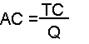
Формула расчёта общих издержек:
Формула расчёта средних постоянных издержек:
Формула расчёта средних переменных издержек:
Формула расчёта выручки:
1)
2)
Формула расчёта бухгалтерской прибыли:
Формула расчёта экономической прибыли:
1)
2)
Формула расчёта рентабельности продукции:
Формула расчёта рентабельности производства:
Формула расчёта предпринимательского дохода:
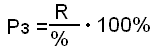
Формула расчёта капиталоотдачи:
Формула расчёта величины циклической безработицы:
Формула расчёта величины естественной безработицы:
Формула расчёта производительности труда:
Формула расчёта дуговой эластичности по доходу:
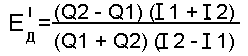
ПРИМЕР ЗАДАЧ
<="" form="">
Коэффициент Джини
Самое краткое определение коэффициента Джини –коэффициент концентрации богатства. Чем он выше – тем выше и неравенство. Более полное определение – мера неравенства распределения доходов. Еще более полное определение – коэффициент девиации экономики от абсолютного равенства в распределении доходов.
Коэффициент выводится из кривой Лоренца и представляет собой отношение площади между этой кривой и линией абсолютного равенства к общей площади под линией абсолютного равенства. Линия абсолютного равенства – биссектриса между осями "доля домохозяйств" и "доля доходов". Коэффициент может быть рассчитан и по точной формуле.
Максимальное значение коэффициента равно единице и это – абсолютное неравенство. Минимальное равно нулю и это абсолютное равенство
В силу социально-политической значимости получаемых на основе коэффициента оценок, он активно рассчитывается, дискутируется и используется для разного уровня выводов. Одна из наиболее активных сфер использования – сравнительный межстрановой и временной анализ. Например, коэффициент Джини для России в 1991 году был равен 0,24, в 2008 году 0,42. В так называемых "образцовых" европейских и особенно североевропейских странах он находится в диапазоне от 0,2 до 0,3.
Но вряд ли уместны прямые заключения из сравнения коэффициента по странам и по времени. У него есть ограничения, переходящие в недостатки, что объясняется двумя обстоятельствами. Во-первых, относительным характером этого показателя. Во-вторых, его диапазонной асимметричностью: одно распределение может быть более равным, чем другое в одном диапазоне, и менее равным в другом при одном том же значении коэффициента для обоих распределений. Поэтому прямые выводы из сравнения коэффициента в разных странах и во временной динамике могут привести к ошибочным оценкам.
Коэффициент назван в честь его автора – итальянца Коррадо Джини (Corradо Gini), преподавателя статистики, социологии и демографии в университете Рима. Коэффициент был предложен им в 1912 году, поэтому у коэффициента намечается знаменательная дата - 100 лет практического использования
Рассчитать коэффициент Джини.
Рассчитать коэффициент Джини:Всего население 1млн100тыс человек.
15%-богатые семьи месячный доход 200 тыс.
35%-средний класс месячный доход 30 тыс.
50%-бедные месячный доход 10 тыс.
Рассчитаем долю доходов бедных семей.
Доход всех семей: 1.1млн*(0.15*200тыс+0.35*30тыс+0.5*10тыс)=1.1млн*(45.5тыс).
Значит доля доходов бедных семей =(1.1млн*(0.5*10тыс)/(1.1млн*(45.5тыс)=0.11.
Таким же образом находим долю доходов среднего класса в общих доходах (равна 0.23).
Значит доля доходов бедных и среднего класса в общих доходах = 0.34.
Индекс Джини я рассчитывал как отношение площади фигуры(S), заключенной между кривой абсолютного равенства и кривой Лоренца, к площади фигуры, заключенной между кривой абсолютного равенства и кривой абсолютного неравенства(Sан=0.5)
S=0.5-S1-S2-S3-S4-S5
S1,S2,S3,S4,S5 можно легко найти по имеющимся данным, а значит можно найти и индекс Джини.
Как найти данные S1,S2,S3,S4,S5,чему они равны?И что делать дальше,как найти именно коэффициент Джини?
· S1,S3,S5 - это прямоугольные треугольники, их площадь находится как половина произведения катетов
S2,S4 - это прямоугольники, их площадь - это произведение сторон
G = 
= 
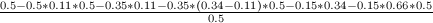= 0.5865
· Некое общество состоит из двух социальных групп, внутри каждой из которых доход распределен равномерно. Известно, что среднедушевой доход в первой группе составляет 5 тыс. руб. в месяц, во второй – 25 тыс. руб. в месяц, а во всем обществе среднедушевой доход составляет 20 тыс. руб. в месяц. Определите значение коэффициента Джини для этого общества.
·
· Решение и ответ
· Обозначим количество членов более бедной социальной группы за 
, более богатой - за 
, а доходы групп соответственно за 
и 
. Тогда:
.
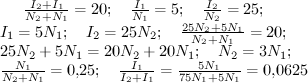Кривая Лоренца будет иметь следующий вид:
· 
· Построив ее, легко посчитать коэффициент Джини:
.
· Ответ:
· 
.
Четырехмерный коктейль
Для приготовления одной порции коктейля "Неустойчивое равновесие" -- фирменного коктейля бара "Economics" -- требуется 1 единица ингредиента A, 2 единицы ингредиента B, 3 единицы ингредиента C и 4 единицы ингредиента D (названия ингредиентов являются коммерческой тайной и не разглашаются). Однако владелец бара, знаменитый бармен и экономист Сэм Полуэльсон, обладает лишь ограниченными ресурсами для закупки дорогих ингредиентов. Так, на имеющиеся у него денежные средства он может купить либо 100 единиц ингредиента A, либо 200 единиц ингредиента B, либо 300 единиц ингредиента C, либо 400 единиц ингредиента D в день.
Какое максимальное число порций фирменного коктейля сможет приготовить Сэм за день?
Мне первым в голову пришло вообще другое решение-логическое
Заметим тот факт,что для покупки любого ингредиента(А,B,C,D) на 1 порцию коктейля нам надо потратить 1/100 всех денег,то-есть на 1 коктейль мы тратим 1/25 всех денег,поэтому всего можем сделать 25 коктейлей
·
