Между интенсивностью распределенной нагрузки, перерезывающей силой и изгибающим моментом существуют дифференциальные зависимости, установленные русским ученым Д.И. Журавским и немецким исследователем М. Шведлером.
| Рисунок 8.17 – К определению дифференциальных зависимостей между элементами изгиба |
и изгибающий момент М, которые при изменении длины на величину dx получают малые приращения d и dМ.
Воспользуемся условие статики для элемента балки dx:
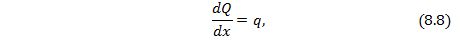
т.е. производная по перерезывающей силе в поперечном сечении по линейной координате х равна интенсивности распределенной нагрузки q в том же сечении. Напомним из высшей математики, что производная функции по координате имеет геометрический смысл тангенса угла наклона касательной к функции по отношению к горизонтальной оси. А значит при криволинейной функции 
, где α-угол между касательной к и горизонтальной линии, параллельной к оси х.
2. 
Для моментов принимаем такое же правило знаков, что и в определении реакций (см. п. 8.2):
откуда, пренебрегая слагаемыми второго порядка малости (подчеркнуто), получаем:
т.е. производная от изгибающего момента в сечении равна перерезывающей силе в том же сечении. Аналогично вышеуказанному, тангенс угла наклона касательной к криволинейной функции М(х) к горизонтальной оси соответствует производной 
Подставляя (8.9) в (8.8) получаем:
т.е. вторая производная от изгибающего момента в сечении равна интенсивности распределенной нагрузки в том же сечении.
Зависимости (8.9) и (8.10) составляют суть теоремы Журавского-Шведлера: первая производная от изгибающего момента равна перерезывающей силе в сечении балки, а вторая производная – интенсивности распределенной нагрузки в том же сечении.
Дифференциальные зависимости между элементами изгиба (8.8)-(8.10) используются при согласовании между собой эпюр и М:
1. На участках балки, на которых перерезывающая сила положительна, изгибающий момент возрастает (слева направо), а на участках, на которых она отрицательна, убывает.
2. Чем больше по абсолютной величине значение перерезывающей силы , тем круче линия, ограничивающая эпюру М. Отсюда следует, что на участке балки с возрастающими (в алгебраическом смысле) слева направо значениями линия, ограничивающая эпюру М, обращена выпуклостью вниз, а с убывающими – выпуклостью вверх.
3. На участке балки, на котором перерезывающая сила имеет постоянное значение, эпюра М ограничена прямой линией.
4. Если на границе соседних участков балки эпюра не имеет скачка, то линии, ограничивающие эпюру М на этих участках, сопрягаются без перелома, т.е. имеют в точке сопряжения общую касательную.
5. Если на границе соседних участков балки на эпюре имеется скачок, то линии, ограничивающие эпюру М на этих участках, сопрягаются с переломами, т.е. не имеют в точке сопряжения общей касательной.
6. Изгибающий момент достигает максимума или минимума в сечениях балки, в которых перерезывающая сила равна нулю; касательная к линии, ограничивающая эпюру М, в этом сечении параллельна оси эпюры.
7. На участках действия распределенной нагрузки q перерезывающие силы изменяются по длине балки (при этом, если интенсивность q постоянна, то перерезывающая сила изменяется по линейному закону); эпюра изгибающих моментов на этих участках ограничены кривыми.
8. На участках балки, на которых распределенная нагрузка отсутствует, перерезывающие силы постоянны, а изгибающие моменты меняются по линейному закону.
9. На участках, где положительный изгибающий момент возрастает, отрицательная перерезывающая сила тоже возрастает; там, где положительный изгибающий момент убывает, положительная перерезывающая сила возрастает.
10. В местах, где к балке приложена сосредоточенная сила, на эпюре будет скачок, равный по величине этой силе, а на эпюре М будет иметь место перелом.
11. Внешний сосредоточенный момент на характере эпюры не отразится, а ордината эпюры М в этом месте изменится скачком, равным по величине этому моменту.
12. Эпюра М всегда обращена выпуклостью навстречу распределенной нагрузке, что следует из формулы (8.10) и совпадения правил знаков для изгибающих моментов и кривизны линии очертания эпюры.
13. Начальные и конечные на эпюрах 
и М должны совпадать со значениями сосредоточенных сил (в том числе реакций) с учетом правила знаков.
Согласование эпюр и М между собой с учетом типичных случаев внешней нагрузки (сосредоточенная и распределенная нагрузка, внешний момент) иллюстрируется следующей таблицей:
Таблица 8.1 – Согласование эпюр и М между собой
