Свойства функций, непрерывных на отрезке

 

Теорема 3.5.(I теорема Больцано-Коши «о нулях функции»)

Если функция f (x) определена и непрерывна на отрезке [ a; b ] и на концах его принимает значения разных знаков, то на этом отрезке найдется хотя бы одна точка с, в которой функция обращается в ноль:
f (c) = 0, a < c < b.

Геометрический смысл этой теоремы в следующем: если непрерывная кривая переходит из одной полуплоскости, на которые ось ОХ разделяет координатную плоскость, на другую, то эта кривая обязательно хотя бы раз пересекает ось ОХ (рис.11).

 

	Рис.11

 

Эта теорема, в частности, находит применение при исследовании существования корня заданного уравнения. Например, выясним, имеет ли корень на отрезке [–1; 1] уравнение

х ³ +5 х +2 = 0.

Рассмотрим функцию f (x) = х ³ +5 х +2. Корень заданного уравнения – это число с такое, что f (c) = 0. Находим f (–1) = –4, f (1) = 8, следовательно, по теореме 3.4, корень уравнения на отрезке [–1; 1] есть, т.е. с Î[–1; 1].

Разделим отрезок пополам: [–1; 0] и [0; 1]. Так как f (0) = 2, то, согласно той же теореме, с Î [–1; 0]. Вновь разделив отрезок [–1; 0] пополам и вычислив значение функции в точке деления, можно найти еще более мелкий отрезок, внутри которого лежит искомое число с.

Продолжая такую операцию, можно найти приближенное значение корня с любой точностью, выбрав в качестве корня любую из границ получившегося малого отрезка. Такой способ отыскания корня называют методом половинного деления (дихотомии).

Теорема 3.6.(II теорема Больцано-Коши «о промежуточном значении»)

Если f (x) определена и непрерывна на отрезке [ a; b ] и на концах принимает отличные друг от друга значения: f (a) = A, f (b) = B, A ≠ B, то для любого числа С, заключенного между А и В, найдется хотя бы одна точка с Î[ a; b ] такая, что f (c) = C.

Смысл этой теоремы в том, что непрерывная функция, принимающая на концах отрезка разные по величине значения А и В, принимает в точках этого отрезка и все промежуточные между А и В значения.

Очевидно, теорема 3.5. есть частный случай теоремы 3.6.

 

Теорема 3.7.(Вейерштрасса)

Если функция f (x) определена и непрерывна на [ a; b ], то она достигает на этом отрезке своих наибольшего и наименьшего значений, т.е. $ с ₁, с ₂Î[ a; b ]: f (c ₁) = m, f (c ₂) = M и m £ f (x) £ M " х Î [ a; b ].

 

Следствие

Непрерывная на отрезке [ a; b ] функция ограничена на нем.

 

Теорема3.8.

Если функция f (x) определена, непрерывна и строго возрастает (убывает) на отрезке [ a; b ], то для нее существует обратная функция f ^–1(x), которая также непрерывна и возрастает (убывает) на соответствующем отрезке.

4 Асимптоты графика функции

Определение 3.5.

Прямая L называется асимптотой кривой Г, если, при удалении точки M(x, y) вдоль кривой Г в бесконечность, расстояние между Г и L стремится к нулю.

Определение 3.6.

Прямая x = a называется вертикальной асимптотой кривой y = f (x), если хотя бы один из пределов f (a + 0) и f (a – 0) бесконечный.

 

 

 

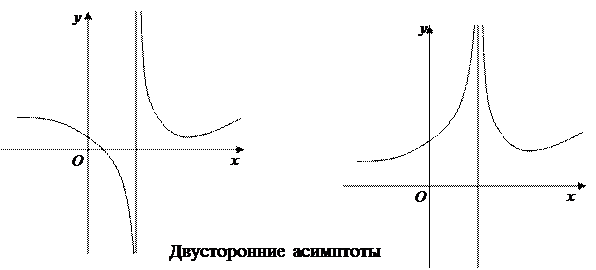Из определения следует, что вертикальными асимптотами графика функ­ции y = f (x) являются прямые x = a, проходящие через точки бесконечного разрыва (II рода) этой функции.

Определение 3.7.

Прямая y = kx + b называется наклонной асимптотой кривой y = f (x) при x ® +¥ (-¥), если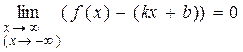

В случае, когда k = 0 наклонная асимптота становится горизонтальной.

Теорема 3.9.

Для того чтобы кривая y = f (x) имела наклонную асимптоту y = kx + b при x ® +¥(-¥), необходимо и достаточно, чтобы

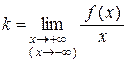и b = .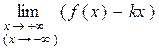

 

Рассмотрим на примере процедуру отыскания асимптот графика заданной функции.

Пример: Найти асимптоты графика функции .

Решение: Область определения функции D(y) = (-¥;0)È(0;¥), значит, x = 0 – точка разрыва этой функции. Исследуем её характер. Вычислим односторонние пределы функции в этой точке:

, ,

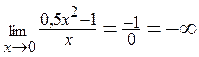значит, x = 0 точка разрыва второго рода, следовательно, прямая x = 0 есть вертикальная асимптота (двусторонняя).

Найдём наклонные асимптоты. Имеем:

,

.

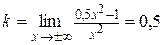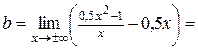
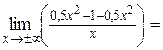
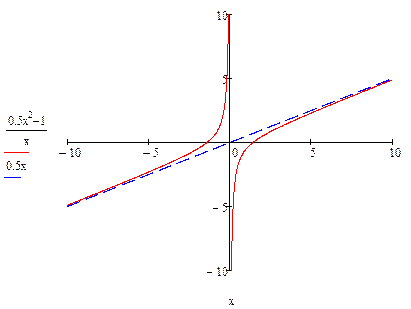
Заметим, что при x ® +¥ разность между данной функцией и функцией у = 0,5 х есть отрицательная бесконечно малая, значит, кривая находится под прямой у = 0,5 х, а при x ® –¥ – над этой прямой.

Таким образом, прямая у = 0,5 х есть наклонная асимптота графика заданной функции (причем двусторонняя, т.е. и при x ® –¥, и при x ® +¥).

Ниже представлен график заданной функции и его асимптоты: