Лекция 3. Непрерывность функции
Содержание лекции: Непрерывность функции в точке. Точки разрыва, их классификация. Непрерывность элементарных функций.
Свойства функций, непрерывных в точке и на отрезке.
Асимптоты графика функции.
1. непрерывность функции в точке.
С понятием предела связано другое важное понятие математического анализа – понятие непрерывности функции.
Когда мы давали определение предела функции в точке х 0, то отмечали, что х 0 – предельная точка области определения функции – может и не принадлежать этой области. Кроме того, когда говорили, что х стремится к х 0, не требовали, чтобы х = х 0, хотя при вычислении предела прежде всего вычисляли значение функции в предельной точке. Особый интерес представляет именно случай, когда х 0ÎD(f), х принимает значение х 0 и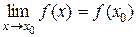 
.
Определение 3.1. Пусть х 0 – точка из области определения функции. Функция у = f (x) называется непрерывной в точке х 0, если
.
Если это условие не выполняется, то функция имеет разрыв в точке х 0
Согласно теореме 2.1(критерию существования предела), 
существует тогда и только тогда, когда существуют односторонние пределы f (x 0+0) и f (x 0–0) и эти пределы равны между собой. Тогда критерий непрерывности функции в заданной точке может быть сформулирован так.
Теорема 3.1.(Критерий непрерывности)
Функция f (x) непрерывна в точке х 0 тогда и только тогда, когда функция определена в этой точке, существуют конечные односторонние пределы f (x 0+0) и f (x 0–0) и выполняется равенство
f (x 0+0) = f (x 0–0) = f (x 0).
Отсюда следует алгоритм исследования непрерывности функции в заданной точке:
1) проверить существование f (x 0);
2) проверить существование конечных односторонних пределов f (x 0+0) и f (x 0–0);
3) проверить равенство f (x 0+0) = f (x 0–0);
4) проверить равенство f (x 0+0) = f (x 0–0) = f (x 0).
Если все условия выполнены, то функция в точке х 0 непрерывна.
Если хотя бы одно условие нарушено, то функция в точке х 0 терпит разрыв.
Определение 3.2.
Точка х 0 называется точкой разрыва первого рода (разрыва с конечным скачком), если существуют конечные односторонние пределы f (x 0+0) и f (x 0–0), но f (x 0+0) ¹ f (x 0–0).
Точка х 0 называется точкой разрыва второго рода, если хотя бы один из односторонних пределов не существует (например, равен ¥).
Точка х 0 называется точкой устранимого разрыва, если существуют конечные пределы f (x 0+0) и f (x 0–0) и
f (x 0+0) = f (x 0–0) ¹ f (x 0).
Из сформулированного выше алгоритма и определения 3.2 следует, что если не выполнено первое условие алгоритма (функция в точке х 0 не определена), то можно только сделать вывод, что в этой точке функция терпит разрыв. Характер же разрыва определяется при проверке условий 2 – 4 алгоритма.
если не выполнено условие 2, то разрыв – второго рода (рис 8 а, б, в).
Если не выполнено условие 3, а условие 2 выполнено, то разрыв – первого рода, при этом условие 1 может быть выполнено (рис.9, а, в), а может быть и не выполнено (рис.9, б). В случае разрыва первого рода число
w = | f (x 0+0) – f (x 0–0)|
называется скачком функции в точке х 0.
 | |||
|
Если выполнены условия 2 и 3, но нарушено условие 4 или 1, то функция имеет устранимый разрыв (рис.10)
Дадим еще одно определение непрерывности функции в точке. Для этого введем следующую терминологию. Если при своем изменении переменная х от значения х 0 перешла к значению х 1, то говорят, что х получила приращение
D х = х 1 – х 0.
При этом функция у = f (x) также получит приращение
D у = f (x 1)– f (x 0) = f (x 0+D х) – f (x 0),
где х 1 = х 0+D х, а f (x 0+D х) = f (x 0) + D у – новое, приращенное, значение функции.
Определение 3. 3. Функция у = f (x) называется непрерывной в точке х 0, если х 0Î D(f) и малому приращению функции соответствует малое приращение аргумента, т.е.
.
Можно доказать, что определения 3.1 и 3.3 эквивалентны. Действительно, если, то " e > 0 $ d > 0 такое, что " х, | x – x 0| < d Þ | f (x) – f (x 0) | < e. Но так как х – х 0 = D х, а f (x)– f (x 0) = D у, то получаем " e > 0 $ d > 0 такое, что " х, |D х | < d Þ | D у | < e. Это значит, что 
.
Наоборот, если , то " e > 0 $ d > 0 такое, что " х, |D х | < d Þ | D у | < e, откуда, учитывая D х = х – х 0 и D у = f (x)– f (x 0), получим " e > 0 $ d > 0 такое, что " х, | x – x 0| < d Þ | f (x) – f (x 0) | < e. А это значит, что . ЧТД.
Определение 3.4. Функция, непрерывная в каждой точке отрезка [ a; b ], называется непрерывной на этом отрезке.
Множество точек, в которых данная функция непрерывна, называют областью непрерывности этой функции.
Непрерывность элементарных функций
Сформулируем основные свойства непрерывных в точке функций в виде теорем.
Теорема 3.2.
Все основные элементарные функции непрерывны в своей области определения.
Доказательство: Рассмотрим, например, линейную функцию у = ах + b. Область определения этой функции (–¥, +¥). Возьмем произвольную точку х = х 0 из области определения, придадим переменной х приращение D х и рассмотрим соответствующее приращение D у функции
D у = (а (х 0 + D х) + b) – (ах + b)) = а D х.
Тогда 
, что, согласно определению 3.3, и означает непрерывность линейной функции в точке х 0, т.е. в произвольной точке области определения.
Аналогично, для функции у = sin x, x Î R. получаем для любого х:
,
что также означает непрерывность функции у = sin x в произвольной точке х области определения.
Для остальных элементарных функций доказательство аналогично.
Теорема 3.3
Если функции f (x) и g (x) определены в области D и непрерывны в точке х 0ÎD, то в этой точке также непрерывны функции f (x) .g (x), f (x) ± g (x), 
, если g (x 0) ¹ 0.
Доказательство: Эти утверждения следуют непосредственно из определения непрерывной в точке функции и свойств пределов (теорема 2.5).
Например, если функции f (x) и g (x) непрерывны в точке х 0, то 
и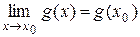 
. Тогда, по теореме 2.5,
,
что и означает непрерывность частного в точке х 0.
Непрерывность суммы, разности и частного доказать самостоятельно.
Теорема 3.4.
Пусть функция j(х) определена на множестве D, а функция f (у) определена на множестве Е(j). Если j(х) непрерывна в точке х 0ÎD, а f (у) непрерывна в точке у 0 = j(х 0), то сложная функция f (j(x)) непрерывна в точке х 0. (без доказательства)
Учитывая определение элементарной функции, из теорем 3.2, 3.3 и 3.4. получаем
Следствие.
Всякая элементарная функция непрерывна в каждой точке, в которой она определена.
Таким образом, областью непрерывности всякой элементарной функции является ее область определения.
Из теоремы 3.4 следует еще одно важное свойство – возможность перехода к пределу под знаком функции:
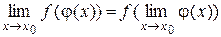
Например,
.
