Рассмотрим интегралы типа 
. С помощью подстановки 
такой интеграл всегда можно преобразовать в интеграл от рациональной дроби относительно переменной t. Действительно, т.к.
при 
, 
,
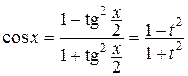х = 2arctg t, 
,
то = 
– под знаком получившегося интеграла стоит рациональная функция, принцип интегрирования которой мы уже обсудили.
Подстановка называется универсальной, так как позволяет тригонометрическую функцию свести к рациональной, но иногда интегрирование получившейся рациональной дроби требует довольно сложных выкладок. Поэтому наряду с универсальной подстановкой рассматривают частные подстановки, которые в некоторых случаях упрощают вычисления.
Функцию R(u (x), v (x)) называют нечетной относительно функции и (х), если R(– u, v) = –R(u, v);
функция R(u (x), v (x)) называют нечетной относительно функции v (х), если R(u, – v) = –R(u, v);
функция R(u (x), v (x))– четная относительно и (х), если R(– u, v) = R(u, v);
функция R(u (x), v (x)) – четная относительно v (х), если R(u, – v) = R(u, v);
если R(– u, – v) = R(u, v), то функция R(u (x), v (x)) четная относительно обеих функций u и v.
А) Если в интеграле функция R (sin x, cos x) – нечетная относительно sin x, то ее можно представить в виде R 1(cos x)sin x, тогда используется подстановка cos x = t:
= 
.
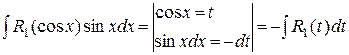Б) Если в интеграле функция R (sin x, cos x) – нечетная относительно cos x, то ее можно представить в виде R 1(sin x)cos x, тогда используется подстановка sin x = t:
= 
.
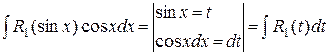В) Если в интеграле функция R (sin x, cos x) – четная относительно sin x и cos x, то она может быть преобразована к виду R 1(tg x) или R 2(сtg x), поэтому используется подстановка tg x = t или ctg x = t соответственно:
=
= 
.
Рассмотрим примеры.
Пример1.
1) Найти 
. Используем универсальную подстановку:
2) Найти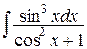 
. Заметим, что функция 
– нечетная относительно sin x. Действительно,
R (–sin x, cos x) = 
= – R (sin x, cos x),
поэтому рациональнее применить не универсальную, а частную подстановку t = cos x:
.
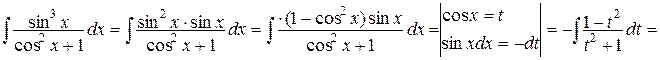
3) Найти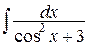 
. В этом случае, подынтегральная функция четная относительно sin x и cos x:
,
поэтому удобно сделать подстановку t = tg x. Получим
.
Г) Рассмотрим интеграл вида 
Если п и т – четные, то для упрощения подынтегрального выражения используются формулы понижения степени:
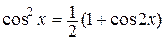
В остальных случаях возможных значений п и т могут быть использованы частные подстановки А), Б), В), а так же другие преобразования подынтегральной функции.
Д) Интегралы вида 
, 
, 
легко вычисляются в результате применения формул
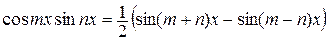
Рассмотрим примеры.
Пример2.
1) 
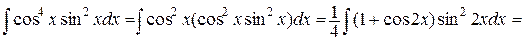
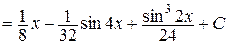
2) 
.
3) 
.
Таким образом, интегрирование тригонометрических функций основано, по существу, на использовании тригонометрических тождеств для преобразования подынтегрального выражения.
