Реферат
На тему
« Уравнения математической физики. Теплопроводность »
Выполнил: студент гр. ПГС-201
Фролов Р.
Проверил: доцент
Баранова И.М.
Брянск 2012 г.
Содержание
Введение. 3
1. Некоторые определения и обозначения. 4
2. Расчет мощности тепловых потерь. 5
2.1 Уравнение теплопроводности. 5
2.2 Мощность тепловых потерь однослойной конструкции. 6
3. Краевые условия. 8
4. Теплопроводность строительных материалов. 16
5. Бетоны и их теплопроводность. 19
6. Зимнее бетонирование. 20
6.1 Приготовление и транспортировка бетонных смесей. 21
6.2 Бетонирование с применением химических добавок. 22
6.3 Метод термоса. 24
6.4 Электропрогрев смеси в конструкциях. 25
6.5 Бетонирование в термоактивной опалубке. 29
6.6 Обогрев бетона инфракрасными лучами. 32
6.7 Охрана труда при производстве бетонных работ. 34
Заключение. 35
Список используемой литературы: 36
Введение
Когда речь заходит о построении математической модели какого-либо явления, принадлежащего к физике, социологии, экономике или другой области знаний, встаёт вопрос о правильном построении системы дифференциальных уравнений и её решения, исходя из начальных или граничных условий.
Математическая физика (МФ) развивалась со времён Ньютона, параллельно развитию физики и математики. В конце 17 века было открыто дифференциальное и интегральное исчисление и сформулированы основные законы классической механики и закон всемирного тяготения. В 18в. Методы МФ начали формироваться при изучении колебаний струн и стержней, а так же задач, связанных с акустикой и гидродинамикой. В 19 веке идеи МФ получили новое развитие в связи с задачами теплопроводности, диффузии, упругости, оптики, электродинамики. В 20 веке в МФ включаются задачи квантовой физики и теории относительности, а так же новые проблемы газовой динамики и переноса частиц.
Многие задачи классической математической физики сводятся к краевым задачам для дифференциальных уравнений – уравнений математической физики. Основными средствами исследования этих задач теория дифференциальных уравнений, теория функций, функциональный анализ.
Изучение математических моделей квантовой физики потребовало привлечения новых областей математики, таких как теория функций комплексного переменного, геометрических, топологических методов.
Некоторые определения и обозначения.
Мы будем рассматривать функцию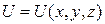 
, полагая, что 
- область в 
Частные производные данной функции мы будем обозначать как 
или 
, а производные второго порядка: 
(
), 
(
)
Определение 1:
Дифференциальным уравнением называется уравнение, содержащее производные неизвестной функции. Если неизвестная функция зависит от одной переменной, то это обыкновенное дифференциальное уравнение, иначе - уравнение в частных производных.
Определение 2:
Наивысший порядок производных неизвестной функции, входящих в уравнение, называется порядком уравнения.
Определение 3:
Дифференциальное уравнение называется линейным, если производные и сама неизвестная функция входят в уравнение линейным образом.
К простейшим уравнениям, рассматриваемым УМФ относятся:
1) 
- уравнение Лапласа 
; 
;
2) 
- волновое уравнение (уравнение колебаний струны) 
;
3) 
- уравнение теплопроводности (диффузии) 
.
Как правило, эти три уравнения являются базовыми, так как уравнения более сложного вида с помощью специальной замены могут быть сведены к ним.
