начинается с определения того, как именно изменяются уровни ряда (увеличиваются, уменьшаются или остаются неизменными) в абсолютном и относительном выражении.
Различают интервальные и моментные ряды динамики. Интервальнымназывается ряд, уровни которого характеризуют значение показателя, достигнутое за определенный период (интервал) времени.
Моментным называется ряд, уровни которого характеризуют значение показателя (явления) по состоянию на определенные моменты времени (дату).
Для этого рассчитывают показатели рядов динамики:
- абсолютные приросты (изменения) уровней;
- темпы роста;
- темпы прироста.
Абсолютный прирост (абсолютное изменение) уровней рассчитывается как разность между двумя уровнями ряда. Он показывает, на сколько (в единицах измерения показателей ряда) уровень одного периода больше или меньше уровня какого-либо предшествующего периода.
В зависимости от базы сравнения абсолютные приросты могут рассчитываться как цепные и как базисные.
Цепные абсолютные изменения уровней ряда за отдельные периоды получаем, вычитая из каждого уровня предыдущий:
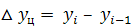(11)
Вычитая из каждого уровня начальный получаем базисные накопленные итоги прироста (изменения) показателя с начала изучаемого периода:
(12)
Темп роста (изменения) Тр- относительный показатель, рассчитываемый как процентное отношение двух уровней ряда (могут выражаться в виде коэффициентов, т.е. простого кратного отношения, и в процентах).
В зависимости от базы сравнения коэффициенты роста (Kр) могут рассчитываться как цепные:
, (13)
и как базисные:
, (14)
где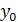 
– начальный уровень ряда динамики, принятый за базу сравнения;
– порядковый член ряда, начиная со второго;
– уровень предшествующего периода.
Темп прироста (снижения) 
– относительный показатель, показывающий, на сколько процентов данный уровень больше (или меньше) другого, принимаемого за базу сравнения. Показатель можно рассчитать:
– путем вычитания 100% из темпа роста (снижения), т.е.
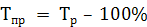; (15)
– как процентное отношение абсолютного прироста к тому уровню, по сравнению с которым рассчитан абсолютный прирост.
Так, темп прироста (цепной) за год будет равен:
(16)
Темп прироста базисный:
(17)
Показатель абсолютного значения 1% прироста (ά) – отношение абсолютного прироста уровня к темпу прироста за соответствующий период:
(18)
Показатель имеет смысл только для цепных абсолютных приростов.
Обобщенной характеристикой динамического ряда может служить средний уровень ряда у.
Средний абсолютный прирост ( изменение ) уровней ( △у) рассчитывается как средняя арифметическая простая из отдельных цепных приростов, т.е.:
(19)
где n – число абсолютных приростов за равные промежутки времени.
Средний абсолютный прирост также может быть рассчитан по формуле:
(20)
Для получения общей характеристики темпа роста показателей за весь период, охватываемый рядом динамики, исчисляется средний темп роста по следующей формуле:
(21)
(22)
где 
– средний темп (коэффициент) роста;
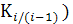– цепные коэффициенты роста;
∏ – знак произведения;
у0 и уп –соответственно начальный (базисный) и конечный абсолютные уровни.
Для определения общей тенденции в рядах динамики составляем табл. 3.
Таблица 3
Расчетные показатели ряда динамики
| Период | Показа-тели | Темпы роста, % | Абсолютный прирост, | Темпы прироста, % | Абсолютные значения 1% прироста, | ||
| цепные | Базис-ные | цепные | Базис-ные | ||||
| У | кр.ц | кр.б | △у | ц△у | б△у | ά | |
Более совершенным методом обработки рядов динамики в целях устранения случайных колебаний и выявления тренда является выравнивание уровней ряда по аналитическим формулам (или аналитическое выравнивание).
В аналитическом выравнивании используем простейшую функцию – линейную (прямую):
(23)
где а и а1 – параметры искомого уравнения по эмпирическим данным.
Анализ рядов динамики заключается в расчете показателей, которые способствуют выявлению общей тенденции развития явления во времени на основе применения аналитического выравнивания рядов динамики по уравнению прямой линии. В табл. 4 приведем пример.
Система нормальных уравнений решается методом наименьших квадратов:
(24)
(25)
Параметры уравнения для рядов динамики рассчитываются:
Таблица 4
Выравнивание ряда динамики по линейной функции
(при счете времени от середины ряда и четном числе уровней)
| Год | Объем промыш-ленной продукции млн руб. | Откло-нение | Квад-ратичное отклонение | Произведе-ние | Выравненный уровень (тренд) уt = а + а 1 t = 21777,8 + 4976,9 t, |
| у | t | t² | уt | уt | |
| - 2 | -31862 | ||||
| - 1 | -16042 | 16800,9 | |||
| 21777,8 | |||||
| 26754,7 | |||||
| 31731,6 | |||||
| Итого |
Втабл. 4 у = уt, следовательно, параметрыуравнения определены верно.
Строится график, где отмечаются фактические и выровненные (расчетные) уровни изучаемого явления по годам, показывающие общую тенденцию развития явления.
Выводы излагаются конкретно по расчетам данной работы. Вносятся конкретные предложения, вытекающие из сделанных расчетов.
Список использованной литературы необходимо привести в соответствии с предъявленными требованиями ГОСТа.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
Основной
1. Ефимова М.Р. Практикум по социальной статистике: учеб. пособие / М.Р. Ефимова, С.Г. Бычков; под ред. М.Р. Ефимовой. – М.: Финансы и статистика, 2005. – 448 с.
2. Статистика: учеб./ И.И. Елисеева [и др.]; под ред. И.И. Елисеевой. – М.: ТК Велби, изд-во «Проспект», 2009. – 448 с.
3. Статистика: учеб./ И.И. Елисеева [и др.]; под ред. И.И. Елисеевой. – М.: ТК Велби, изд-во «Проспект», 2006. – 448 с.
4. Теория статистики: учеб. / под ред. проф. Г.А. Громыко. – 2-е изд., перераб. и доп. – М.: ИНФРА-М, 2006. – 476 с.
5. Социально-экономическая статистика: учеб. пособие / И.И. Колесникова. – 2-е изд., испр. – Минск: Новое знание, 2007. – 260 с.
6. Статистические сборники: «Российский статистический ежегодник», «Регионы России», «Группа восьми» в цифрах», «Инвестиции в России», «Научная и инновационная деятельность регионов Сибирского федерального округа», «Россия и страны - члены Европейского союза» и др.
