Рассмотрим расчет параметров уравнения регрессии между стоимостью основных фондов х и валовым выпуском продукции у.
Исходные данные и расчет приведем в табл. 2.
Пре д положим, что зависимость между показателями х и у линейная, т.е.
Таблица 2
Расчетная таблица для определения параметров уравнения регрессии
по индивидуальным данным
| Основные фонды, млн руб. х | Валовой выпуск продукции, млн руб. у | х2 | ху | _ у х = -10,24 + + 2,12х |
| ∑x = 520 | ∑у = 1000 | ∑ x ²=35624 | ∑ ух =70244 | ∑ух =1000 |
Параметры а и b этого уравнения найдем, решив систему нормальных уравнений (5). Подставив в нее необходимые суммы, рассчитанные в табл. 2, получим
10 a + 520 b = 1000,
520 a + 35624 b = 70244.
Решив систему уравнений, найдем, что а = -10,24, b = 2,12. Отсюда искомое уравнение регрессии у по х будет
y x = -10,24 + 2,12 х.
Подставляя в данное уравнение последовательно значения х (12, 16, 25 и т.д.), нахо д им теоретические (выравненные) значения результативного признака, т.е. y x, которые показывают, каким теоретически должен быть средний объем валового выпуска продукции при данной стоимости основных фондов хi (при прочих равных условиях для всех предприятий). Теоретические значения y x приведены в последней графе табл. 2 (с округлением до целых).
Для нахождения а и b при линейной зависимости могут быть предложены готовые формулы.
Так, на основе определителей 2-го порядка из системы нормальных уравнений (5) получим:
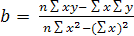, (6)
или, разделив каждое уравнение на n в системе нормальных уравнений (12), и путем дальнейших преобразований получим:
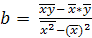(7)
или
(8)
следовательно, 
В рассматриваемом примере найдем параметр b по формуле
Рассчитав 
= 520/10 = 52 и у = 1000 / 10 = 100, легко найти а:
а = 
Параметр b, т.е. коэффициент при х, в уравнении линейной регрессии называется коэффициентом регрессии.
Коэффициент регрессии показывает, на сколько (в абсолютном выражении) изменяется значение результативного признака у при изменении факторного признака х на единицу.
По данным корреляционной таблицы необходимо рассчитать линейный коэффициент корреляции по формуле
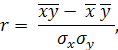
где σх и σу – соответственно среднее квадратическое отклонение в ряду х и в ряду у.
,
.
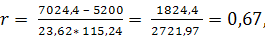
т.е. между х и у связь выше средней.
r < 0,3 – малая зависимость;
0,3 < r < 0,6 - средняя зависимость;
0,6 < r < 0,8 - зависимость выше средней;
r > 0,8 – большая, сильная зависимость.
Эмпирическая линия регрессии, отражающая на графике зависимость между х и у, не всегда дает основание для выдвижения гипотезы о линейной зависимости. Характер ломаной линии может быть различным.
