Основные характеристики функции
1. Определение 1.3. Функция  , определенная на множестве D, называется четной, если
, определенная на множестве D, называется четной, если 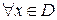 выполняются условия
выполняются условия  и
и  ; нечетной, если
; нечетной, если 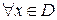 выполняются условия
выполняются условия  и
и 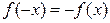 .
.
График четной функции симметричен относительно оси Oy, а нечетной – относительно начала координат.
Например,  – четные функции,
– четные функции,  – не-четные функции,
– не-четные функции,  – функции общего вида, т.е. ни четные и ни нечетные.
– функции общего вида, т.е. ни четные и ни нечетные.
2. Пусть функция  определена на множестве D и пусть
определена на множестве D и пусть  .
.
Определение 1.4. Если для любых значений  аргументов из неравенства
аргументов из неравенства  вытекает неравенство:
вытекает неравенство:
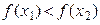 , то функция называется возрастающей на множестве
, то функция называется возрастающей на множестве  ;
;
 , то функция называется неубывающей на множестве
, то функция называется неубывающей на множестве  ;
;
 , то функция называется убывающей на множестве
, то функция называется убывающей на множестве  ;
;
 , то функция называется невозрастающей на множестве
, то функция называется невозрастающей на множестве  .
.
Возрастающие, невозрастающие, убывающие и неубывающие функции на множестве  называются монотонными на этом множестве, а возрастающие и убывающие – строго монотонными. Интервалы, в которых функция монотонна, называются интервалами монотонности.
называются монотонными на этом множестве, а возрастающие и убывающие – строго монотонными. Интервалы, в которых функция монотонна, называются интервалами монотонности.
3. Определение 1.5. Функция  , определенная на множестве D, называется ограниченной на этом множестве, если существует такое число
, определенная на множестве D, называется ограниченной на этом множестве, если существует такое число  , что для всех
, что для всех  выполняется неравенство
выполняется неравенство  .
.
Отсюда следует, что график ограниченной функции лежит между прямыми  и
и  . Например, функция
. Например, функция  ограничена на всей числовой прямой, так как
ограничена на всей числовой прямой, так как  для любого x.
для любого x.
4. Определение 1.6. Функция  , определенная на множестве D, называется периодической на этом множестве, если существует такое число T, что при каждом
, определенная на множестве D, называется периодической на этом множестве, если существует такое число T, что при каждом  значение
значение  и
и  .
.
Число T называется периодом функции. Если T – период функции, то ее периодами будут также числа  , где
, где  . Так, например, для функции
. Так, например, для функции  периодами будут числа
периодами будут числа  , при этом наименьшим положительным периодом будет
, при этом наименьшим положительным периодом будет  . Вообще, обычно наименьшее положительной число T, удовлетворяющее неравенству
. Вообще, обычно наименьшее положительной число T, удовлетворяющее неравенству  , берут за основной период.
, берут за основной период.
Обратная функция
Пусть задана функция  с областью определения D и множеством значений E.
с областью определения D и множеством значений E.
Определение 1.7. Если каждому значению  соответствует единственное значение
соответствует единственное значение  , то определена функция
, то определена функция  с областью определения E и множеством значений D. Такая функция
с областью определения E и множеством значений D. Такая функция  называется обратной к функции
называется обратной к функции  и записывается в следующем виде:
и записывается в следующем виде:  .
.
Про функции  и
и  говорят, что они являются взаимно обратными. Чтобы найти функцию
говорят, что они являются взаимно обратными. Чтобы найти функцию  , обратную к функции
, обратную к функции  , достаточно решить уравнение
, достаточно решить уравнение  относительно x (если это возможно).
относительно x (если это возможно).
Например, для функции  обратной функцией является функция
обратной функцией является функция  ; для функции
; для функции  , обратной функцией является
, обратной функцией является  ; для функции
; для функции  , заданной на отрезке
, заданной на отрезке  , обратной не существует, т.к. одному значению y соответствует два значения x: если
, обратной не существует, т.к. одному значению y соответствует два значения x: если  , то
, то  .
.
Из определения обратной функции вытекает, что функция  имеет обратную тогда и только тогда, когда функция
имеет обратную тогда и только тогда, когда функция  задает взаимно однозначное соответствие между множествами D и E. Отсюда следует, что любая строго монотонная функция имеет обратную. При этом, если функция возрастает (убывает), то обратная функция также возрастает (убывает).
задает взаимно однозначное соответствие между множествами D и E. Отсюда следует, что любая строго монотонная функция имеет обратную. При этом, если функция возрастает (убывает), то обратная функция также возрастает (убывает).
Заметим, что функция  и обратная ей
и обратная ей  изображаются одной и той же кривой, т.е. графики их совпадают. Если же условиться, что, как обычно, независимую переменную (т.е. аргумент) обозначить через x, а зависимую переменную через y, то функция обратная функции
изображаются одной и той же кривой, т.е. графики их совпадают. Если же условиться, что, как обычно, независимую переменную (т.е. аргумент) обозначить через x, а зависимую переменную через y, то функция обратная функции  запишется в виде
запишется в виде  .
.
Графики взаимно обратных функций  и
и  симметричны относительно биссектрисы первого и третьего координатных углов, уравнение которой имеет вид:
симметричны относительно биссектрисы первого и третьего координатных углов, уравнение которой имеет вид:  .
.
Сложная функция
Определение 1.8. Пусть функция  определена на множестве D, а функция
определена на множестве D, а функция  на множестве
на множестве  , причем для
, причем для 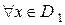 соответствующее значение
соответствующее значение  . Тогда на множестве
. Тогда на множестве  определена функция
определена функция  , которая называется сложной функцией от x (или суперпозицией заданных функций, или функцией от функций)
, которая называется сложной функцией от x (или суперпозицией заданных функций, или функцией от функций)
Переменную  называют промежуточным аргументом сложной функции.
называют промежуточным аргументом сложной функции.
Например, функция  есть суперпозиция двух функций
есть суперпозиция двух функций  и
и 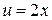 . Сложная функция может иметь несколько промежуточных аргументов.
. Сложная функция может иметь несколько промежуточных аргументов.
Основные элементарные функции и их графики
Основными элементарными функциями называются функции, которые имеет следующий вид, и на рисунках представлены их графики.
1. Линейная функция
Функция вида y=ax+b, где a, b Î R называется линейной функцией.
Графиком линейной функции является прямая. Для построения прямой достаточно знать координаты двух точек, например, A (0; b) и  , если a ¹0.
, если a ¹0.

Коэффициент k называют угловым коэффициентом прямой – графика функции y=kx+b.
2. Квадратичная функция
Функция вида  , где a, b, c Î R, называется квадратичной функцией.
, где a, b, c Î R, называется квадратичной функцией.
Графиком квадратичной функции является парабола.
 |
a >0 – ветви параболы направлены вверх; a <0 – ветви параболы направлены вниз.
Точка (xв; yв) – вершина параболы,  .
.
Прямая x = xв – ось симметрии.
x 1, x 2 – корни квадратного уравнения  .
.
3. Обратная пропорциональность
Функция вида  , где k ≠0, x ≠0 называется обратной пропорциональностью.
, где k ≠0, x ≠0 называется обратной пропорциональностью.
Графиком данной функции является гипербола.

4. Степенные функции
1). Степенная: 

2). Степенная: 

5. Показательные функции
Функция, заданная формулой y=ax, где a >0, a ¹1, называется показательной функцией с основанием a.

6. Логарифмические функции
Функция, заданная формулой  называется логарифмической функцией с основанием a.
называется логарифмической функцией с основанием a.

7. Тригонометрические функции
Тригонометрическими функциями называются функции вида!.

8. Обратные тригонометрические функции
Обратными тригонометрическими функциями называются функции вида!.

Функция, задаваемая одной формулой, составленной из основных элементарных функций и постоянных с помощью конечного числа арифметических операций (сложения, вычитания, умножения, деления) и операций взятия функции от функции, называются элементарными функциями. Например, следующие функции являются элементарными:

Примерами неэлементарных функций могут служить функции:
 .
.
2. ПРЕДЕЛ ФУНКЦИИ
2.1. Предел функции в точке
Пусть функция  определена на некотором числовом множестве X и точка
определена на некотором числовом множестве X и точка  является предельной точкой этого множества, т.е. в любой e -окрестности точки
является предельной точкой этого множества, т.е. в любой e -окрестности точки  содержатся точки множества X, отличных от
содержатся точки множества X, отличных от  . Точка
. Точка  может принадлежать множеству X или не принадлежать ему, следовательно, функция
может принадлежать множеству X или не принадлежать ему, следовательно, функция  либо определена в точке
либо определена в точке  , либо не определена.
, либо не определена.
Определение 2.1. (на «языке e-d», или по Коши).
Число A называется пределом функции  в точке
в точке  (или при
(или при  ), если для любого положительного e найдется такое положительное число d, что для всех
), если для любого положительного e найдется такое положительное число d, что для всех  , удовлетворяющих неравенству
, удовлетворяющих неравенству  , выполняется неравенство
, выполняется неравенство 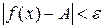 .
.
С помощью логических символов это определение можно записать следующим образом:
 .
.
Геометрический смысл предела функции: 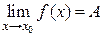 , если для любой e -окрестности точки A найдется такая d -окрестность точки
, если для любой e -окрестности точки A найдется такая d -окрестность точки  , что для всех
, что для всех  из этой d- окрестности соответствующие значения функции
из этой d- окрестности соответствующие значения функции  лежат в e -окрестности точки A. Иными словами, точки графика функции
лежат в e -окрестности точки A. Иными словами, точки графика функции  лежат внутри полосы шириной 2 e, ограниченной прямыми
лежат внутри полосы шириной 2 e, ограниченной прямыми  . Очевидно, что величина d зависит от выбора e, поэтому пишут
. Очевидно, что величина d зависит от выбора e, поэтому пишут  .
.
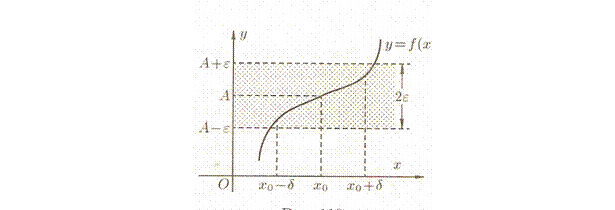
Еще раз подчеркнем, что при решении вопроса о существовании предела функции f в точке  сама точка
сама точка  из рассмотрения исключается, а функция f считается определенной в некоторой достаточно малой окрестности точки
из рассмотрения исключается, а функция f считается определенной в некоторой достаточно малой окрестности точки  . В этом смысле свойство функции иметь предел в точке является локальным свойством функции.
. В этом смысле свойство функции иметь предел в точке является локальным свойством функции.
Пример 2.1. Доказать, что
 .
.
Решение. Возьмем произвольное  , найдем
, найдем  такое, что для всех x, удовлетворяющих неравенству
такое, что для всех x, удовлетворяющих неравенству  , выполняется неравенство
, выполняется неравенство  .
.
 .
.
Обозначив  , видим, что для всех x, удовлетворяющих неравенству
, видим, что для всех x, удовлетворяющих неравенству  , где
, где  , выполняется неравенство
, выполняется неравенство  . Следовательно,
. Следовательно,  .
.
,
2.2. Предел функции при 
Сформулируем понятие предела функции при  , т.е. когда x неограниченно возрастает по модулю.
, т.е. когда x неограниченно возрастает по модулю.
Определение 2.2. Число A называется пределом функции  при
при  , если для любого положительного e существует такое положительное число
, если для любого положительного e существует такое положительное число  , что при всех
, что при всех  , удовлетворяющих неравенству
, удовлетворяющих неравенству  , выполняется неравенство
, выполняется неравенство 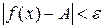 .
.
С помощью логических символов это определение можно записать следующим образом:
 .
.
Если  , то пишут
, то пишут  ; если
; если  , то пишут
, то пишут  .
.
Геометрический смысл этого определения таков: для  , что при
, что при  или
или  соответствующие значения функции
соответствующие значения функции  попадают в e -окрестность точки A, т.е. точки графика лежат в полосе шириной 2 e, ограниченной прямыми
попадают в e -окрестность точки A, т.е. точки графика лежат в полосе шириной 2 e, ограниченной прямыми  .
.






