Объединение четного семейства множеств является счетным множеством
A1= 
A2= 
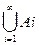
An=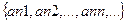 
Q= 
Q1= 
Qk= 
Q=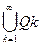 
Несчетность множества вещественных чисел.
Теорема: R несчетно.
Доказательство от противного:
1<->х1=[х1], х11 х12 х13... |
2<->х2=[х2], х21 х22 х23... | Пусть здесь нет девяток в периоде
3<->х3=[х3], х31 х32 х33... |
... | (*)
к<->хк=[хк ], хк1 хк2 хк3... |
... |
Найдем число которого нет в таблице:
с=[с], с1 с2 с3...
[с]≠[х1] => с≠х1
с1 
{9;х21} => с≠х2
с2 {9;х32} => с≠х3
...
ск {9;хк+1к} => с≠хк
Таким образом число С отсутствует в табл (*)
Мощность булеана счетного множества.
Теорема: Для всякого множества |M|<|B(M)|
Док:
1 |M|<=|B(M)| выделим в B(M) одноэлементные подмножества S
f: M->s; f(a)={a}
2 |M|≠|B(M)|
f:M->B(M) взаимно однозначны
f(m)⊂M
T={m:m f(m)}⊂ M
T=f(y) y 
M
y T? y T?
y f(y)=T y f(y)=T
Вещественные числа. Отношение порядка на множестве вещественных чисел.
Отношение строгого порядка a<b (a0=b0,a1=b1,ai<bi)
антирефлексивно (a, b разные числа), антисимметрично (a<b, b<a неверно), транзетивно (a<b, b<c).
Теорема о точной верхней грани.
Определение: АÌR mÎR, m - верхняя (нижняя) грань А, если " аÎА а£m (а³m).
Определение: Множество A ограничено сверху (снизу), если существует такое m, что " аÎА, выполняется а£m (а³m).
Определение: SupA=m, если 1) m - верхняя грань A
2) " m’: m’<m => m’ не верхняя грань A
InfA = n, если 1) n - нижняя грань A
2) " n’: n’>n => n’ не нижняя грань A
Определение: SupA=m называется число, такое что: 1) " aÎA a£m
2) "e>0 $ aEÎA, такое, что aE>a-e
InfA = n называется число, такое что: 1) 1) " aÎA a³n
2) "e>0 $ aEÎA, такое, что aE<a+e
Теорема: Любое, непустое ограниченное сверху множество АÌR, имееет точную верхнюю грань, причем единственную.
Доказательство:
Построим на числовой прямой число m и докажем что это точная верхняя грань А.
[m]=max{[a]:aÎA} [[m],[m]+1]ÇA¹Æ=>[m]+1 - верхняя грань A
Отрезок [[m],[m]+1] - разбиваем на 10 частей
m1=max[10*{a-[m]:aÎA}]
m2=max[100*{a-[m],m1:aÎA}]
...
mк=max[10K*{a-[m],m1...mK-1:aÎA}]
[[m],m1...mK, [m],m1...mK + 1/10K]ÇA¹Æ=>[m],m1...mK + 1/10K - верхняя грань A
Докажем, что m=[m],m1...mK - точная верхняя грань и что она единственная:
"к: [m’K,m”K)ÇA¹0; "к "аÎА: а<m”K
Единственность(от противного):
аÎА, пусть а>m”K => $ к: а’K>m”K => а³а’K>m”K - это противоречит ограниченности => a£m
Точная верхняя грань:
Пусть l<m, тогда $ к: m’K>l”K, но так как "к [m’K,m”K) ÇA¹0 => $ аÎ[m’K,m”K) => а>l =>l - не верхняя грань.
Теорема: Любое, непустое ограниченное снизу множество АÌR, имееет точную нижнюю грань, причем единственную.
Рассмотрим множество B{-а: аÎА}, оно ограничено сверху и не пусто => $ -SupB=InfA
