ИССЛЕДОВАНИЕ ПРОЦЕССА ФИЛЬТРОВАНИЯ НА ЭЛЕМЕНТЕ ВАКУУМ-ФИЛЬТРА
Цель работы
Определение констант фильтрования, удельного сопротивления осадка и сопротивления фильтровальной перегородки.
Содержание работы
1. Ознакомиться с закономерностями фильтрования с образованием слоя несжимаемого осадка.
2. Изучить методику определения констант фильтрования.
3. Провести опыты по разделению модельных суспензий.
4. Построить по опытным данным график зависимости τ/g=f (g) и определить значения констант фильтрования, удельное сопротивление осадка в сопротивление фильтровальной перегородки.
Теоретическая часть
3.1. Основные понятия и термины.
В работе используются следующие понятия я термины:
суспензия, фильтрование, фильтр, фильтровальная перегородка, осадок, фильтрат, схема устройства и принцип работы простейшего фильтра;
способ создания разности давления при фильтровании;
материалы, применяющиеся для изготовления фильтровальных перегородок;
фильтрование с образованием слоя осадка, сжимаемые и несжимаемые осадки, фильтрование с закупориванием пор, промежуточное фильтрование, фильтрование с применением вспомогательных веществ;
скорость фильтрования, фильтрование при постоянной разности давления, при постоянной скорости и при переменных значениях давления и скорости;
удельный объем фильтрата, сопротивление осадка и перегородки, удельное сопротивление осадка, константы фильтрования.
Перед выполнением лабораторной работы необходимо уяснить содержание этих терминов и понятийно учебнику (1, стр. 194—198, 205—206) и дополнительному теоретическому материалу, изложенному в настоящих методических указаниях.
3.2. Скорость фильтрования и факторы, влияющие на ее величину при образовании слоя несжимаемого осадка на фильтровальной перегородке
Важным показателем работы фильтра является скорость фильтрования, определяемая как объем фильтрата, проходящего в единицу времени через единицу поверхности фильтровальной перегородки
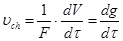(9.1)
где V — объем полученного фильтрата;
τ— время фильтрования;
F — площадь поверхности фильтровальной перегородки;
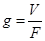— удельный объем фильтрата (объем фильтрата, полученный с единицы поверхности фильтрования).
Скорость фильтрования прямо пропорциональна разности давлений и обратно пропорциональна вязкости фильтрата и общему сопротивлению фильтрования
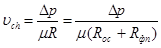(9.2)
где ∆р — разность давлений по обе стороны фильтровальной перегородки;
μ — вязкость фильтрата;
R = Rос + R — общее сопротивление фильтра;
Roc — сопротивление осадка;
Rфп — сопротивление фильтровальной neрегородки.
Сопротивление осадка можно определить как
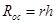(9.3)
где r — удельное сопротивление осадка;
h — толщина осадка.
Объем осадка, полученного на фильтровальной перегородке, равен
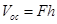(9.4)
Отношение полученных объемов влажного осадка и фильтрата обозначимкак
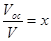(9.5)
На основании выражений (9.4) и (9.5) получаем
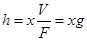(9.6)
и тогда на основании (9.3) сопротивление осадка определится как
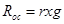(9.7)
Подставив это значение сопротивления осадка в уравнение (9.2), получим следующеевыражение для скорости фильтрования
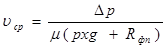(9.8)
Из полученного выражения следует, что при прочих равных условиях скорость фильтрования тем больше и производительность фильтра тем выше, чем меньше удельный объём полученного фильтрата или пропорциональная этому объему толщина слоя осадка на фильтровальной перегородке. Поэтому для повышения производительности фильтра необходимо стремиться к скорейшему удалению осадка с фильтровальной перегородки. Для фильтров непрерывного действия это равносильно требованию удалять с фильтровальной перегородки слой осадка наименьшей толщины.
Если сопротивление фильтровальной перегородки мало и можно принять, что Rфп ≈0, то на основании уравнения (9.8) получим
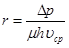(9.9)
Из этого выражения следует, что удельное сопротивление осадка численно равно разности давлений, необходимой для того, чтобы фильтрат, вязкость которого равна единице, протекал со скоростью, равной единице, через слой осадка единичной толщины. Таков физический смысл понятия «удельное сопротивление осадка».
В системе СИ размерность удельного сопротивления осадка равна м-2, тогда размерности общего сопротивления фильтра, сопротивлений осадка и фильтровальной перегородки будут м-'.
Удельное сопротивление осадка является важнейшей и самой сложной физической величиной в теории фильтрования. Действие различных факторов на процесс фильтрования всегда может быть сведено к изменению величины удельного сопротивления осадка под действием этих факторов. Все факторы, влияющие на процесс фильтрования суспензий, в общем случае можно подразделить на гидродинамические и физико-химические. Гидродинамические факторы - это пористость осадка, размер частиц, их удельная поверхность, сферичность и равномерность укладки. Физико-химические факторы — это степень коагуляций и пептизации твердых частиц суспензии; содержание в ней смолистых и коллоидных примесей, закynopивающих поры ocaдка; влияние элёктрокинетического потенциала, возникающего на границе раздела твердой и жидкой фаз и уменьшающего сечение пор; наличие сольватной оболочки на частицах осадка. Вследствие совместного проявления гидродинамических и физико-химических факторов невозможно вычислить аналитически величину удельного сопротивления осадка как функцию всех указанных выше факторов, поэтому величину удельного сопротивления - осадка определяют опытным путем.
3.3. Уравнение фильтрования при постоянной разности давлений
Рассмотрим некоторые закономерности фильтрования при постоянной разности давления с образованием несжимаемого осадка на несжимаемой фильтровальной перегородке. Выражая в уравнении (9.8) скорость фильтрования согласно (9.1), разделяя переменные (удельный объем фильтрата и время) и интегрируя полученное дифференциальное уравнение в пределах от 0 до g и от 0 до τ, получим следующее расчетное уравнение фильтрования, известное как уравнение Рутса.
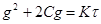(9.10)
где «C» и «K» — размерные комплексы, составленные из постоянных для процесса фильтрования величин. Эти комплексы называют константами фильтрования и их значения равны
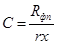(9.11) и 
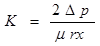(9.12)
В выражения (9.11) и (9.12) входят удельное сопротивление осадка г и фильтровальной перегородки Rфп. Величину удельногосопротивленияосадка, как было указано ранее, не удается определить расчетным путем, и ее находят экспериментально, не удается рассчитать и сопротивление фильтровальной перегородки, поэтому значения констант фильтрования определяют экспериментально. Процессы фильтрования, которые при прочих равных условиях отличаются только значениями перепада давления, будут характеризоваться равными значениями константы К.
Переменными величинами в уравнении (9.10) являются время процесса фильтрования τ и удельный объем фильтрования 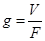. Решив это уравнение относительно удельного объема, можно для заданной продолжительности процесса фильтрования определить объем полученного фильтрата как V=gF. Уравнение (9.10) позволяет решить и обратную задачу: при известном удельном объеме фильтрата рассчитать продолжительность процесса фильтрования.
3.4. Уравнение фильтрования при постоянной скорости процесса
При фильтровании с постоянной скоростью объем фильтрата, полученного на фильтре за время τ, можно определить как V=vфFτ, и тогда удельный объем фильтрата определится как
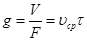(9.13)
Подставив это значение удельного объема фильтрата в уравнение (9.8) и решив его относительно ∆р, получим расчетное уравнение для определения перепада давления в фильтре к моменту времени фильтрования τ
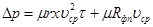(9.14)
Если ∆р задано, то на основании этого уравнения можно определить время, в течение которого будет достигнута эта разность давления при фильтровании с поcтоянной скоростью. Для выполнения расчетов с помощью уравнения (9.14) необходимо знать значения удельного сопротивления осадка и сопротивление фильтровальной перегородки.
3.5. Определение констант фильтрования, удельного сопротивления осадка и сопротивления фильтровальной перегородки
Поделив левую и правую части уравнения (9.10) gK, получим
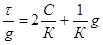(9.15)
Так как значения величин μ, r,x, Rфп и ∆р в процессе фильтрования при постоянной разности давления остаются неизменными, то уравнение (9.15) в координатах τ/g и g является уравнением прямой линии, наклоненной к оси абсцисс под углом, тангенс которого равен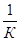 
, и отсекающей на оси ординат (при g=0) отрезок, равный 
.
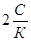Для определения констант фильтрования проводят опыт по разделению суспензии с помощью фильтра при постоянной разности давления. В течение опыта замеряют ряд соответствующих друг другу значений g и τ. По данным опыта в координатах τ/g÷g наносят точки, через которые наилучшим образом проводят прямую линию, для которой определяют тангенс угла наклона α и отрезок А, отсекаемый ею на оси ординат. По этим данным рассчитывают значения констант как
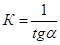(9.16)
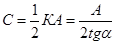(9.17)
Зная константы фильтрования, можно на основании выражений (9.11) и (9.12) определить удельное сопротивление осадка и сопротивление фильтровальной перегородки как
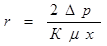(9.18)
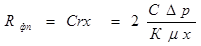(9.19)
Определив удельное сопротивление осадка и зная х, можно рассчитать величину константы К для фильтрования при других значениях разности давления.
Описание лабораторной установки
Установка для проведения лабораторных исследований, процесса фильтрования (рис. 9.1) состоит из погружного элемента вакуум-фильтра 1, емкости для суспензии 2 с мешалкой 3, ресивера 9, вакуум-насоса 10, мерной емкости для сбора фильтрата 7 и вакуумметра 6. Отдельные части установки соединены между собой вакуумными резиновыми трубками, как показано на рис. 9.2. Для управления работой установки служат краны 5 и 8.
Кран 11 служит для слива фильтрата из мерной емкости 7 после окончания работы. Мешалка 3 предназначена для перемешивания суспензии с целью предотвращения осаждения твердых частиц и образования осадка на дне емкости. Температура суспензии определяется с помощью термометра 4.
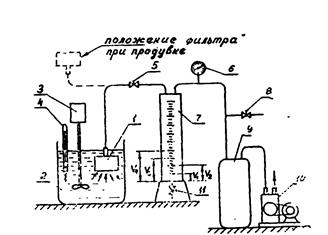
Рис. 9.1. Схема установки:
1 —элемент вакуум-фильтра; 2— емкость, 3—. мешалка; 4— термометр; 5. 8, II— краны; 6— вакуумметр; 7—мерная емкость для сбора фильтрата; 9—ресивер; 10—вакуум-насос
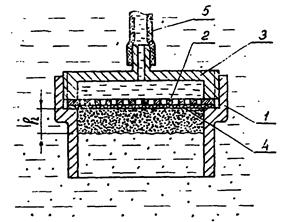
Рис. 9.2. Элемент вакуум-фильтра:
/—корпус; 2 — решетка; 3—крышка; 4—фильтровальная перегородка; 5—резиновая трубка
Элемент вакуум-фильтра (рис. 9.2) состоит из цилиндрического корпуса 1, съемной решетки 2, нажимной крышки 3 и фильтровальной перегородки 4, в качестве которой используется фильтровальная ткань. С помощью вакуумной резиновой трубки 5 элемент вакуум-фильтра сообщается с емкостью для сбора фильтрата.
Перед началом работы внешним осмотром убедиться в исправном состоянии всех элементов установки, проверить надежность крепления резиновых шлангов на штуцерах. Для предотвращения разбрызгивания жидкости мешалкой ее лопасти должны быть погружены в жидкость, но не касаться дна. Во время работы мешалки запрещается касаться ее вала.
До начала опыта получить инструктаж от лаборанта о порядке включения и выключения мешалки и вакуум-насоса и в присутствии лаборанта сделать их пробные включения и выключения.
К работе приступить только после получения на это разрешения от лаборанта.
