Цель работы
Целью данной работы является:
Ø изучение основных видов описания типовых динамических звеньев линейных систем автоматического регулирования: передаточными функциями, переходными и частотными характеристиками, весовыми функциями, корневыми годографами;
Ø исследование статических, динамических и частотных характеристик инерционного звена второго порядка;
Ø изучение взаимной связи между различными видами описания инерционного звена второго порядка;
Ø исследование влияния параметров передаточной функции инерционного звена второго порядка на его статические и динамические свойства.
Задание
1. Исследовать влияние параметров передаточной функции инерционного звена второго порядка на переходную, амплитудно-частотную и фазочастотную характеристики.
2. Построить переходную, логарифмические амплитудно-частотную и фазочастотную характеристики (ЛАХ и ФЧХ), амплитудно-фазовую характеристику (годограф, или АФЧХ) и амплитудно-частотную характеристику (АЧХ) в линейном масштабе инерционного звена второго порядка для различных значений параметров передаточной функции при помощи программного комплекса МВТУ.
3. Сформулировать и записать в отчет выводы о влиянии параметров передаточной функции инерционного звена второго порядка на его статические и динамические свойства и на частотные характеристики.
Краткие сведения из теории автоматического управления
Инерционным звеном второго порядка (колебательным звеном) называют элементы, процессы в которых описываются дифференциальным уравнением второго порядка
(1)
или в операторной форме
(T 22 s 2 + T 1 s + 1)z вых (t) = Kх(t)
Отсюда передаточная функция инерционного звена второго порядка
(2)
где К – статический передаточный коэффициент; Т 1, Т 2 – постоянные времени звена.
Встречается в литературе и другая запись передаточной функции инерционного звена второго порядка (такая запись используется в программном комплексе МВТУ):
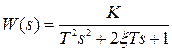, (3)
где К – статический передаточный коэффициент; Т – постоянная времени звена, x - коэффициент затухания колебаний (в программе обозначен как b).
Нетрудно установить связь между параметрами К, Т, Т 1, Т 2 и x этих передаточных функций. Для этого достаточно приравнять множители при одинаковых степенях s в числителе и знаменателе и получить:
1) статические передаточные коэффициенты передаточных функций (2) и (3) строго равны друг другу;
2) постоянная времени Т в передаточной функции (3) равна постоянной времени Т 2 в записи (2);
3) постоянная времени Т 1 в передаточной функции (2) связана с постоянной времени Т в передаточной функции (3) соотношением
.
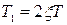В общем случае передаточная функция на основании общего вида уравнения движения САР может быть представлена в виде отношения многочленов от s:
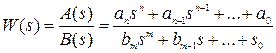
(4)
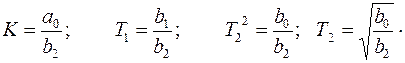
Связь между параметрами передаточной функции вида (2) и коэффициентами многочленов числителя и знаменателя в выражении (4) можно получить, приравнивая правые части выражений для передаточной функции. Тогда для инерционного звена второго порядка будем иметь:
Ниже при описании свойств колебательного звена используется передаточная характеристика вида (2).
Переходную характеристику инерционного звена второго порядка можно определить на основании общего решения дифференциального уравнения второго порядка (1):
(5)
Корни характеристического уравнения l1 и l2, представляющего собой знаменатель передаточной функции (2)
T 22 s 2 + T 1 s + 1 = 0
определяются соотношением для обычного квадратного уравнения:
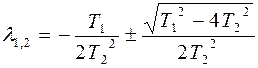
(6)
Постоянные интегрирования определяются из начальных условий:
при t = 0 h(t) = 0; dh/dt = 0. С учетом начальных условий можно получить для постоянных интегрирования два уравнения:
С 1 + С 2 = 0, (7)
l 1 С 1 + l 2 С 2 = 0.
Из системы уравнений (7) находятся обе постоянные интегрирования.
Следовательно, переходная функция инерционного звена второго порядка будет выражаться уравнением
(8)
В зависимости от соотношения постоянных Т 1, Т 2 корни характеристического уравнения l1, l 2 могут принимать различные значения. Поэтому характер переходного процесса также будет зависеть от соотношения постоянных времени Т 1, Т 2.
Характер переходного процесса можно оценить коэффициентом затухания колебаний (иногда называется коэффициентом демпфирования):
На основании сравнения передаточных функций колебательного звена вида (2) и вида (3) нетрудно получить, что величина x, используемая в записи передаточной функции (3) строго равна d 0, т.е. d 0 = x.
С использованием d 0 корни характеристического уравнения могут быть представлены в виде
Если d 0 > 1, т.е. (Т 1 > 2T 2 ), то корни характеристического уравнения вещественные отрицательные:
 |
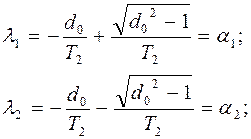Характер переходного процесса будет апериодический.
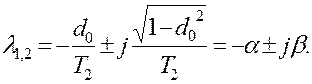
Если d 0 < 1, т.е. (Т 1 < 2Т 2 ) корни характеристического уравнения будут комплексные сопряженные с отрицательной вещественной частью.
Переходная функция инерционного звена второго порядка для рассматриваемого вида корней будет представлена уравнением
(7)
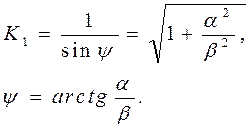
Где
Переходная функция (характеристика) имеет колебательный характер (затухающая синусоида с частотой b). Следует отметить, что затухание колебаний происходит интенсивнее при увеличении коэффициента затухания d 0и увеличении постоянной времени Т 1.
 |
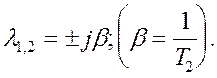При d 0 = 0 (T 1 = 0, T 2 >0) инерционное звено второго порядка преобразуется в гармоническое звено. При этом корни характеристического уравнения становятся чисто мнимыми и сопряженными.
Переходная функция гармонического звена принимает вид
h(t) = K(1 - cosw 0 t) (8)
АФЧХ инерционного звена второго порядка имеет вид
(9)
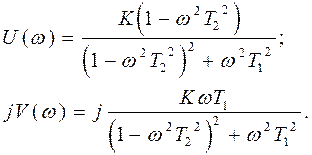
Вещественная и мнимая части АФЧХ инерционного звена второго порядка
Можно показать, что АФЧХ в координатах U(w), V(w) при изменении w от нуля до бесконечности для различных значений коэффициента затухания d0 имеют вид, представленный на рис. 1.
 |
Примерами инерционных звенев второго порядка могут служить цепь постоянного тока с сопротивлением R, индуктивностью L и емкостью С; электродвигатель постоянного тока; акселерометр маятникового типа с торсионом; электромашинный усилитель ЭМУ и др. элементы.
 |
Рассмотрим цепь постоянного тока с R, L, C (рис.2).
Если такую цепь подключить к постоянному напряжению U вх = const, то уравнение движения (в данном примере – переходный процесс в последовательном контуре) можно записать следующим образом
(10)
 |
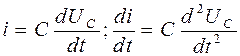Учитывая, что для емкости
Уравнение (10) можно записать следующим образом
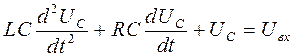
(11)
Полагая, что входной величиной является U вх, а выходной величиной – напряжение на конденсаторе U c, уравнение (11) в операторной форме будет выглядеть так
(LCs 2 + RCs + 1)U c = U вх.
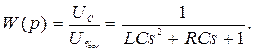
Передаточная функция рассматриваемой цепи
Или
 |
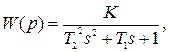Где К – статический передаточный коэффициент;
T 1 = RC – первая постоянная времени, с;
– вторая постоянная времени, с.
Можно отметить, что первая постоянная времени связана с затратами энергии в звене (в сопротивлении R), а вторая постоянная времени T 2 характеризует способность звена накапливать и рекупировать (отдавать) энергию в звене.
Если положить R = 0 (или пренебречь им), то получится гармоническое звено (Т 1 = 0), в котором возникают незатухающие колебания.
Порядок выполнения работы
