Определитель матрицы обозначается стандартным математическим символом |A|. Чтобы ввести оператор нахождения определителя матрицы, можно нажать кнопку Determinant (Определитель) на панели инструментов Matrix (Матрица) или набрать на клавиатуре <|> (нажав клавиши <Shift>+<\>). В результате появляется местозаполнитель, в который следует поместить матрицу. Чтобы вычислить определитель уже введенной матрицы, нужно:
- Переместить курсор в документе таким образом, чтобы поместить матрицу между линиями ввода.
- Ввести оператор нахождения определителя матрицы.
- Ввести знак равенства, чтобы вычислить определитель.
Обратная матрица
Поиск обратной матрицы возможен, если матрица квадратная и ее определитель не равен нулю. Произведение исходной матрицы на обратную по определению является единичной матрицей. Для ввода оператора поиска обратной матрицы нажмите кнопку Inverse (Обратная матрица) на панели инструментов Matrix (Матрица).
Решение матричных уравнений
Рассмотрим систему n линейных алгебраических уравнений относительно n неизвестных x1, x2,…,xn.
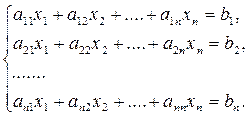 (1)
(1)
В соответствии с правилом умножения матриц рассмотренная система линейных уравнений может быть записана в виде:  , где:
, где:
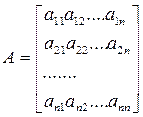
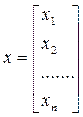

Если определитель матрицы А не равен 0, то система имеет единственное решение, т.к. существует обратная матрица А-1 при умножении обеих частей уравнения на которую получаем:
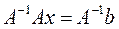
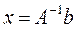
Системы линейных уравнений удобно решать с помощью функции lsolve:
lsolve(А, b)- возвращается вектор решения x такой, что  (см. рис. 9).
(см. рис. 9).
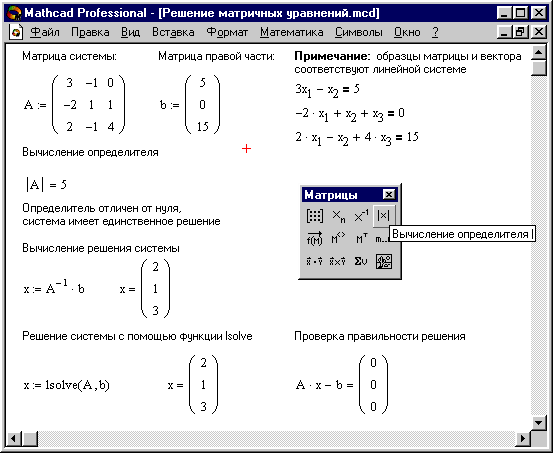
Рис.9.
Метод Гаусса
Метод Гаусса состоит в том, что систему (1) приводят последовательным исключение неизвестных к эквивалентной системе с треугольной матрицей:
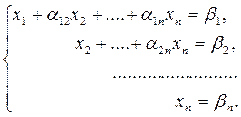
решение которой находят по рекуррентным формулам:
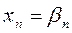 ,
, 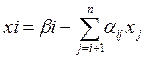
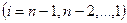
В матричной записи это означает, что сначала (прямой ход метода Гаусса) элементарными операциями над строками приводят расширенную матрицу системы к ступенчатому виду:
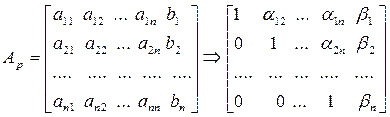
а затем (обратный ход метода Гаусса) эту ступенчатую матрицу преобразуют так, чтобы в первых n столбцах получилась единичная матрица:
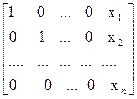
Последний, (n+1) этой матрицы содержит решение системы (1).
В Mathcad прямой и обратный ходы метода Гаусса выполняет функция rref(A). На рис.10 показано решение системы линейных уравнений методом Гаусса, в котором используются следующие функции:
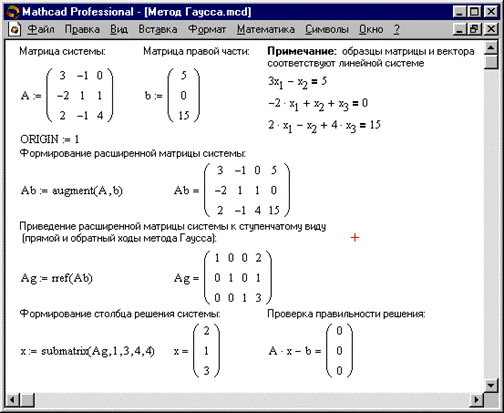
Рис. 10
rref(A) - возвращает ступенчатую форму матрицы А.
augment(A, В) - возвращает матрицу, сформированную слиянием матриц-аргументов слева направо. Массивы A и В должны иметь одинаковое число строк.
submatrix(A, ir, jr, ic, jc) - возвращает матрицу, состоящую из всех элементов с ir по jr строкуи столбцах с ic по jc. Удостоверьтесь, что ir ≤ jr и ic ≤ jc, иначе порядок строк и (или) столбцов будет обращен.
Создание графиков
В Mathcad встроено несколько различных типов графиков, которые можно разбить на две большие группы:
Ø Двумерные графики
- XY (декартовый) график,
- полярный график;
Ø Трехмерные графики
- график трехмерной поверхности,
- график линий уровня,
- трехмерная гистограмма,
- трехмерное множество точек,
- векторное поле.
Чтобы создать график, например двумерный декартовый, необходимо:
1) Поместить курсор ввода в то место, куда требуется вставить график.
2) Нажмите на панели Graph (График) кнопку X-Y Plot для создания Декартового графика.
3) В результате в обозначенном месте документа появится пустая область графика с местозаполнителями, в один из которых нужно ввести функцию, а имя аргумента в другой.
В результате Mathcad создает график функции в пределах значений аргумента, по умолчанию принятых равными от –10 до 10.






