Оценки сезонной компоненты

Задание.

Постройте график динамики исследуемого показателя в зависимости от года.
Вычислите коэффициенты автокорреляции уровней ряда до 6-го порядка включительно. Постройте график автокорреляционной функции (коррелограмму).
С учетом коррелограммы и динамики ряда выявите структуру временного ряда.
Постройте аддитивную модель временного ряда. Укажите коэффициент детерминации модели.
Постройте мультипликативную модель временного ряда. Укажите коэффициент детерминации модели.
Представьте динамику уровней исходного ряда и двух построенных рядов (по аддитивной и мультипликативной моделям) на одном графике.
Постройте прогнозное значение показателя на 2015 и 2016 год по двум моделям.

Приложение.

Построение аддитивной модели временнόго ряда.

Рассмотрим данные об объеме потребления электроэнергии жителями некоторого района (данные колонки 1 и 2 табл.1). Из анализа автокорреляционной функции
ясно, что данный временнóй ряд содержит сезонные колебания периодичностью в четыре квартала. Объемы потребления электроэнергии в осенне-зимний период (I и IV кварталы) выше, чем весной и летом (II и III кварталы).

Таблица 1

Выравнивание уровней ряда методом скользящей средней

№ квартала	Потребление электро- энергии, y_t	Итого за четыре квартала	Скользящая средняя за четыре квартала	Центрированная скользящая средняя	Оценка сезонной компоненты
	6,0
	4,4
	5,0	24,4	6,10	6,25	–1,250
	9,0	25,6	6,40	6,45	2,550
	7,2	26,0	6,50	6,625	0,575
	4,8	27,0	6,75	6,875	–2,075
	6,0	28,0	7,00	7,1	–1,100
	10,0	28,8	7,20	7,3	2,700
	8,0	29,6	7,40	7,45	0,550
	5,6	30,0	7,50	7,625	–2,025
	6,4	31,0	7,75	7,875	–1,475
	11,0	32,0	8,00	8,125	2,875
	9,0	33,0	8,25	8,325	0,675
	6,6	33,6	8,40	8,375	–1,775
	7,0	33,4	8,35
	10,8

По графику этого ряда можно установить наличие приблизительно равной амплитуды колебаний. Это говорит о возможном наличии аддитивной модели. Рассчитаем ее компоненты.

Шаг 1. Проведем выравнивание исходных уровней ряда методом скользящей средней.

Поскольку циклические колебания имеют периодичность в четыре квартала, просуммируем уровни ряда последовательно за каждые четыре квартала со сдвигом на один момент времени и определим условные годовые объемы потребления электроэнергии (колонка 3 в табл.1).

Разделив полученные суммы на 4, найдем скользящие средние (колонка 4 табл.1). Полученные таким образом выравненные значения уже не содержат сезонной компоненты.

Поскольку скользящие средние получены осреднением четырех соседних уровней ряда, т.е. четного числа значений, они соответствуют серединам подынтервалов, состоящих из четверок чисел, т.е. должны располагаться между третьим и четвертым значениями четверок исходного ряда. Для того чтобы скользящие средние располагались на одних временных отметках с исходным рядом, пары соседних скользящих средних еще раз усредняются и получаются центрированные скользящие средние (колонка 5 табл.1). При этом теряются первые две и последние две отметки временнόго ряда, что связано с осреднением по четырем точкам.

Шаг 2. Найдем оценки сезонной компоненты как разность между фактическими уровнями ряда (колонка 2 табл. 1) и центрированными скользящими средними (колонка 5). Эти значения помещаем в колонку 6 табл.1 и используем для расчета значений сезонной компоненты (см. табл.2), которые представляют собой средние за каждый квартал (по всем годам) оценки сезонной компоненты S_i. В моделях с сезонной компонентой обычно предполагается, что сезонные воздействия за период (в данном случае – за год) взаимопогашаются. В аддитивной модели это выражается в том, что сумма значений сезонной компоненты по всем точкам (здесь – по четырем кварталам) должна быть равна нулю.

Таблица 2

Оценки сезонной компоненты

Показатели	Год	№ квартала, i
I	II	III	IV
		–	–	–1,250	2,550
		0,575	–2,075	–1,100	2,700
	0,550	–2,025	–1,475	2,875
	0,675	–1,775	–	–
Итого за i -й квартал (за все годы)		1,800	–5,875	–3,825	8,125
Средняя оценка сезонной компоненты для i -го квартала,		0,600	–1,958	–1,275	2,708
Скорректированная сезонная компонента,	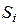	0,581	–1,977	–1,294	2,690

Для данной модели сумма средних оценок сезонной компоненты равна:

0,6–1,958–1,275+2,708=0,075.

Эта сумма оказалась не равной нулю, поэтому каждую оценку уменьшим на величину поправки, равной одной четверти полученного значения:

Δ=0,075/4=0,01875.

Рассчитаем скорректированные значения сезонной компоненты (они записаны в последней строке табл.2):

Эти значения при суммировании уже равны нулю:

0,581–1,977–1,294+2,69=0.

Шаг 3. Исключаем влияние сезонной компоненты, вычитая ее значения из каждого уровня исходного временнόго ряда. Получаем величины:

T+E=Y–S.

Эти значения рассчитываются в каждый момент времени и содержат только тенденцию и случайную компоненту (колонка 4 табл. 3).

Таблица 3