Лабораторная работа 6 - Экспоненциальное сглаживание временных рядов
Цели и задачи лабораторной работы
В данной лабораторной работе проведем построение и прогнозирование динамики среднедушевых денежных доходов населения за период 1999-2006гг. (р. в мес.) с помощью метода экспоненциального сглаживания, при этом будут решаться следующие задачи:
1) Построим адаптивную модель с помощь простого экспоненциального сглаживания;
2) Построим экспоненциальную модель с учетом тренда;
3) Построим экспоненциальную модель с учетом тренд-сезонной составляющей.
Проводя расчеты, воспользуемся информацией с 1 квартала 1999г. по 4 квартал 2005г., имеющиеся данные за 2006г. будем использовать для сравнения с выровненными уровнями (приложение Л).
Понятие экспоненциального сглаживания временных рядов
Разработку метода экспоненциального сглаживания приписывают Р. Г. Брауну, данный метод характерен тем, что при его применении изменяют каждый уровень yt, учитывая сам этот уровень и предшествующие ему, причем «вклад» предшествующего уровня тем меньше, чем «старше» этот уровень. Веса уровней снижаются экспоненциально в степени, зависящей от принятой величины параметра сглаживания a, значение которого находится в пределах 0-1.
При обсуждении вопроса о возможности применения метода экспоненциального сглаживания для прогнозирования экономических процессов остановимся на следующих важных моментах.
1) Метод экспоненциального сглаживания, разработанный для анализа временных рядов, состоящих из большого числа наблюдений, при изучении экономических временных рядов нередко не «срабатывает». Это обусловлено тем, что экономические временные ряды бывают слишком короткими (15-20 наблюдений) и в случае, когда темпы роста и прироста велики, то, как показывает практика, метод не «успевает» отразить все изменения.
2) Для нахождения оценок коэффициентов сглаживающего полинома используется рекуррентная процедура, позволяющая при конечном числе наблюдений получить приближенное решение задачи, причем приближение тем точнее, чем больше число наблюдений.
3) Проблема выбора начальных условий принципиально, сводится к оценке погрешности метода, а вопрос выбора оптимального значения параметра сглаживания a для своего решения требует, прежде всего, четкой постановки задачи.
Рассмотрим содержание процедуры экспоненциального сглаживания, а также ее модификации, разработанные с учетом различной структуры временного ряда - наличие тренда и сезонных изменений.
Рекомендуемая литература
Для лучшего понимания материала изложенного в данной главе необходимо дополнительно проанализировать следующие источники литературы (см. список использованных источников):
| Номер в списке литературы | Страницы |
| 3.3 | 125-130 |
| 3.4 | 53-65 |
| 3.10 | 60-85 |
Простое экспоненциальное сглаживание (метод Брауна)
Проиллюстрируем метод простого экспоненциального сглаживания используя следующие сглаживающие константы: a = 0,1; a = 0,5; a = 0,9.
Прежде чем приступить к построению данной модели необходимо сказать, что все методы анализа временных рядов (в том числе и экспоненциальное сглаживание) в пакете собраны в модуле Time series & Frication (Временные ряды и прогнозирование).
Для запуска метода экспоненциального сглаживания в пакете STATISTICA необходимо:
Шаг 1. В главном меню программы выбрать Statistics®Advanced Linear/Nonlinear Models® Time series/Frication (Статистика ® Выбор линейных/нелинейных моделей ® Временные ряды и прогнозирование).
Шаг 2. В появившемся окне Time Series Analysis (рисунок 6.1) необходимо выбрать кнопку Exponential smoothing & forecasting (Экспоненциальное сглаживание и прогнозирование), после чего перейдем в окно Seasonal and Non-Seasonal Exponential smoothing (Сезонное и не сезонное экспоненциальное сглаживание).

Рисунок 6.1 – Окно выбора методов анализа временных рядов

Рисунок 6.2 – Окно настроек моделей экспоненциального сглаживания
где: Seasonal component – опция задает лаг (задержку) сезонной компоненты;
None – в данном столбце собраны модели не учитывающие сезонную составляющую;
Additive – в столбце отображены модели содержащие аддитивную сезонную составляющую;
Multiplicative – в столбце отображены модели содержащие мультипликативную сезонную составляющую;
No trend – в данной строке представлены модели не содержащие;
Linear trend – модели содержащие линейный тренд;
Exponential – модель содержащие экспоненциальный тренд;
Damped trend – затухающий тренд
Alpha – константа простого экспоненциального сглаживания;
Delta – константа отвечающая за сезонность;
Gamma – константа отвечающая за тренд;
Phi – константа
Шаг 3. Для построения модели с параметрам a=0,1, необходимо установить флажок на пересечении опций None и No trend. В поле Alpha указать 0,1, далее нажать кнопку Summary: Exponential smoothing (Провести экспоненциальное сглаживание). Результаты оценивания модели становятся доступны в новом окне Workbook (Рисунок 6.3).
В верхней части графика выводится сообщение об уровне, с которого начинается сглаживание, в данном случае программа автоматически выбрала S0 =4300. Далее указывается, что модель построена без учета тренд и сезонной составляющей (No trend, no season), при этом сглаживающая константа равна 0,1 (Alpha =0,100).
На графике отображены две оси ОY, по левой отложены значения исследуемой переменной, по правой даны значения отклонений (Residuals) фактических уровней от выровненных. Пунктирной линией на графике отображены сглаженные значения (Smoothed Series) изучаемого ряда, точечной линией – отклонения (Resids).
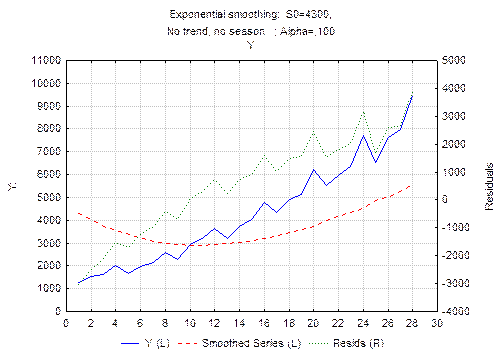
Рисунок 6.3 - Графики сглаженного временного ряда среднедушевых денежных доходов населения при a=0,1.
Аналогичные вычисления проведем для a= 0,5 и a = 0,9.

Рисунок 6.4 - Графики сглаженного временного ряда среднедушевых денежных доходов населения при a=0,5

Рисунок 6.5 - Графики сглаженного временного ряда среднедушевых денежных доходов населения при a=0,9
Анализируя приведенные графики нетрудно заметить, что чем меньше значение сглаживающей константы, тем меньше варьируют сглаженные значения. При малой величине a= 0,1 сглаженные значения сильно расходятся с фактическими уровнями исходного временного ряда. В общем случае сглаживание при малых a слабо реагирует на подобные скачки или поворотные точки. Большая константа a= 0,9 дает гораздо меньший сглаживающий эффект, однако сглаженные значения в большей степени следуют фактическим значениям по всей длине исходного временного ряда.
Константа a= 0,5 дает промежуточный эффект между первыми двумя вариантами. Это подтверждает тот факт, что использовать большие константы следует для рядов, содержащих незначительную нерегулярную компоненту.
Заметим также, что анализируемый показатель имеет тенденцию к росту, а также сезонную составляющую с максимумом в 4 квартале каждого года.
Основная цель экспоненциального сглаживания, как и любого другого метода исследования временных рядов, является прогнозирование уровней ряда на k -уровней вперед (не стоит исключать случаи прогнозирования на k -уровней назад).
Для построения прогноза на основе модели экспоненциальной средней в СПП STATISTICA 6.0 необходимо в окне Seasonal and Non-Seasonal Exponential smoothing выбрать вкладку Advanced (Расширенные).

Рисунок 6.6 – Окно установок для прогнозирования (приведена часть исходного окна)
Для установки периода упреждения необходимо в поле Forecast ___ cases (Прогнозировать на k значений) установить необходимое значение, в нашем случае установим число 4 (что соответствует четырем кварталам 2006г.). Все результаты оценивания модели представим в таблице 6.1.
Согласно полученным прогнозным значениям, представленным в таблице 6.1, варианты прогноза по модели с параметром 0,5 и 0,9 практически не отличаются друг от друга, также среднеквадратическое отклонение в данных случаях ниже, чем в первом. Отсюда можно сделать вывод, что наилучшие прогнозы, по-видимому, будут получены по моделям с высокими значениями сглаживающей константы. Но вместе с тем необходимо указать на то, что рассчитанные значения показателей значительно расходятся с фактическими значениями. Объясняется данное явление тем, что в анализируемом ряду содержится тренд и сезонная составляющая.
Таблица 6.1 – Результаты прогнозирования уровней ряда среднедушевых денежных доходов населения с помощью экспоненциального сглаживания
| Квартал/год | Модели | ||||
| Фактические значения | a=0,1 | a=0,5 | a=0,9 | ||
| I/2006 | 7873,0 | 5938,40 | 8508,93 | 9298,35 | |
| II/2006 | 9575,8 | 5938,40 | 8508,93 | 9298,35 | |
| III/2006 | 9988,2 | 5938,40 | 8508,93 | 9298,35 | |
| IV/2006 | - | 5938,40 | 8508,93 | 9298,35 | |
| Среднеквадратическое отклонение | - | 3445955,49 | 907204,43 | 739004,78 | |






