На практике, для идентификации мультиколлениарности, наиболее часто прибегают к анализу матрицы парных коэффициентов корреляции. В паккете STATISTICA 6.0. данную процедуру можно реализовать двумя способами:
Первый способ:
Шаг 1. Выберем в главном меню Statistics ® Basic Statistics/Tables (Статистика ® Основные статистики и таблицы).
Шаг 2. В окне Basic Statistics and Tables выбреем пункт Correlation matrices (Корреляционная матрица) и нажмем кнопку ОК.
Шаг 3. В окне Moment and Partial Correlations выберем кнопку One variables list и выделим переменные для анализа Y, X1-X5, далее нажмем Summary (Итоги).
Таблица 4.1 – Матрица коэффициентов корреляции (первый способ)
| Y | X1 | X2 | X3 | X4 | X5 | |
| Y | 1,000 | -0,194 | 0,737 | -0,070 | 0,792 | -0,165 |
| X1 | -0,194 | 1,000 | -0,123 | 0,666 | -0,154 | 0,566 |
| X2 | 0,737 | -0,123 | 1,000 | -0,189 | 0,678 | -0,264 |
| X3 | -0,070 | 0,666 | -0,189 | 1,000 | -0,152 | 0,313 |
| X4 | 0,792 | -0,154 | 0,678 | -0,152 | 1,000 | -0,160 |
| X5 | -0,165 | 0,566 | -0,264 | 0,313 | -0,160 | 1,000 |
Второй способ:
Шаг 1. В главном меню выберем Statistics ® Multiple Regression в окне Multiple Linear Regressions нажмем кнопку Variables (Зависимая переменная – Y, не зависимые – X1, X2, X3, X4, X5)
Шаг 2. Установим флажок напротив опции Review descriptive statistics, correlation matrix и нажмем кнопку ОК.
Шаг 3. В окне Review descriptive statistics (во вкладке Advanced) выберем кнопку Correlations (Корреляция).
Согласно данным, приведенным в таблице 4.2 (таблица 4.1), между переменными X2 и X4, а также X1 и X3, X5 наблюдается сильная взаимосвязь (0,678, 0,666 и 0,566 соответственно), что свидетельствует о наличии мультиколлениарности. В связи с этим при оценке модели с переменными X2 и X4 (оказывают сильное воздействие на Y) невозможно разделить влияние данных переменных на зависимую переменную, т.е. мы не можем одновременно включить переменную в модель.
Таблица 4.2 - Матрица коэффициентов корреляции (второй способ)
| X1 | X2 | X3 | X4 | X5 | Y | |
| X1 | 1,000 | -0,123 | 0,666 | -0,154 | 0,566 | -0,194 |
| X2 | -0,123 | 1,000 | -0,189 | 0,678 | -0,264 | 0,737 |
| X3 | 0,666 | -0,189 | 1,000 | -0,152 | 0,313 | -0,070 |
| X4 | -0,154 | 0,678 | -0,152 | 1,000 | -0,160 | 0,792 |
| X5 | 0,566 | -0,264 | 0,313 | -0,160 | 1,000 | -0,165 |
| Y | -0,194 | 0,737 | -0,070 | 0,792 | -0,165 | 1,000 |
Еще одни распространенным способом выявления наличия мультиколлениарности является расчет показателей детерминации, для этого последовательно необходимо оценить пять уравнений регрессии.
В этом случае зависимая переменная Y исключается из рассмотрения, и уравнение принимает вид - 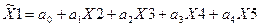
Воспользуемся модулем Multiple Regression получим следующие результаты:
Таблица 4.3 - Показатели адекватности множественного уравнения регрессии влияния независимых переменных на фактор X1
| Value | |
| Multiple R | 0,776 |
| Multiple R? | 0,602 |
| Adjusted R? | 0,549 |
| F(4,30) | 11,329 |
| p | 0,000 |
| Std.Err. of Estimate | 1984,209 |
Согласно данным, приведенным в таблице 4.3, получаем значение коэффициента детерминации R2 X1 | X2, X3, X4, X5 равное 0,602.
Оценивая оставшиеся четыре регрессионных уравнения, получаем следующие результаты:
R2 X1 | X2, X3, X4, X5 = 0,602
R2 X2 | X1, X3, X4, X5 = 0,506
R2 X3 | X1, X2, X4, X5 = 0,469
R2 X4 | X1, X2, X3, X5 = 0,472
R2 X5 | X1, X2, X3, X4 = 0,380
Анализируя коэффициенты можно сделать вывод, что значимая связь наблюдается между всеми показателями (кроме X5) и остальными независимыми показателями, т.е. в очередной раз подтверждается наличие в имеющихся данных мультиколлениарности.






