Метод экспоненциального сглаживания

Очевидно, что в методе взвешенного скользящего среднего существует множество способов задавать значения весов так, чтобы их сумма была равной 1. Один из таких способов называется экспоненциальным сглаживанием. В этой схеме метода взвешенного среднего для любого t > 1 прогнозируемое значение в момент времени t+1 представляет собой взвешенную сумму фактического объема продаж , за период времени t и прогнозируемого объема продаж , за период времени t Другими словами,

.

Экспоненциальное сглаживание имеет вычислительные преимущества перед скользящим средним. Здесь, чтобы вычислить , необходимо знать только значения , и , (вместе со значением α). Например, если компании нужно спрогнозировать спрос для 5000 наименований изделий в каждый период времени, то в этом случае необходимо хранить 10001 значений данных (5000 значений , 5000 значений , и значение α), в то время как для выполнения прогноза на основе скользящего среднего по 8 узлам требовалось 40000 значений данных. В зависимости от поведения данных, возможно, потребуется хранить различные значения α для каждого изделия, но даже в этом случае количество хранимой информации значительно меньше, чем при использовании скользящего среднего. Положительная особенность экспоненциального сглаживания состоит в том, что, сохраняя α и последний прогноз, все предыдущие прогнозы также неявно сохраняются.

Рассмотрим некоторые свойства модели экспоненциального сглаживания. Для начала заметим, что если t > 2, то в формуле (1) t можно заменить на t–1, т.е. Подставив это выражение в первоначальную формулу (1), получим

.

Выполняя последовательно аналогичные подстановки, получим следующее выражение для

. (2)

Поскольку из неравенства 0 < α < 1 следует, что 0 < 1 – α < 1, то Другими словами, наблюдение , имеет больший вес, чем наблюдение , которое, в свою очередь, имеет больший вес, чем 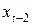. Это иллюстрирует основное свойство модели экспоненциального сглаживания — коэффициенты при убывают при уменьшении номера k. Также можно показать, что сумма всех коэффициентов (включая коэффициент при 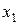), равна 1.

Из формулы (2) видно, что значением является взвешенная сумма всех предыдущих наблюдений (включая последнее наблюдение ). Последнее слагаемое суммы (2) является не статистическим наблюдением, а «предположением» (можно предположить, например, что ). Очевидно, что с ростом t влияние , на прогноз уменьшается, и в определенный момент им можно будет пренебречь. Даже если значение α достаточно малое (такое, что (1 – α) приблизительно равно 1), значение будет быстро убывать.

Значение параметра α сильно влияет на функционирование модели прогнозирования, поскольку α представляет собой вес самого последнего наблюдения . Это значит, что следует назначать большее значение α в том случае, когда в модели наиболее прогностическим является именно последнее наблюдение. Если же α близко к 0, это означает практически полное доверие к прошлому прогнозу и игнорирование последнего наблюдения.

Перед Виктором возникла проблема: как наилучшим образом подобрать значение α. Вновь, в этом поможет средство Поиск решения. Чтобы найти оптимальное значение α (т.е. такое, при котором прогнозная кривая будет менее всего отклоняться от кривой значений временного ряда), выполните следующие действия.

1. Выберите команду Сервис -> Поиск решения.
2. В открывшемся диалоговом окне Поиск решения установите целевую ячейку G16 (см. лист «Экспо») и укажите, что ее значение должно быть минимальным.
3. Укажите, что изменяемой ячейкой является ячейка В1.
4. Введите ограничения В1 > 0 и B1 < 1
5. Щелкнув на кнопке Выполнить, получите результат, показанный на рис. 8.

Рис. 8

Опять, как и в методе взвешенного скользящего среднего, наилучший прогноз будет получен, если назначить весь вес последнему наблюдению. Следовательно, оптимальное значение α равно 1, при этом среднее абсолютных отклонений равно 6,82 (ячейка G16). Виктор получил прогноз, который уже видел ранее.

Метод экспоненциального сглаживания хорошо работает в ситуациях, когда интересующая нас переменная ведет себя стационарно, а ее отклонения от постоянного значения вызваны случайными факторами и не носят регулярного характера. Но: вне зависимости от значения параметра α методом экспоненциального сглаживания не удастся спрогнозировать монотонно возрастающие или монотонно убывающие данные (прогнозируемы значения будут всегда меньше или больше наблюдаемых, соответственно). Также можно показать, что в модели с сезонными изменениями получить удовлетворительные прогнозы этим методом не удастся.

Если статистические данные монотонно изменяются или подвержены сезонным изменениям, необходимы специальные методы прогнозирования, которые будут рассмотрены ниже.

Метод Хольта (экспоненциальное сглаживание с учетом тренда)

,

где

,

.

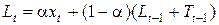Метод Хольта позволяет прогнозировать на k периодов времени вперед. Метод, как видно, использует два параметра α и β. Значения этих параметров находятся в пределах от 0 до 1. Переменная L, указывает на долгосрочный уровень значений или базовое значение данных временного ряда. Переменная Т указывает на возможное возрастание или убывание значений за один период.

Рассмотрим работу этого метода на новом примере. Светлана работает аналитиком в большой брокерской фирме. На основе имеющихся у нее квартальных отчетов компании Startup Airlines она хочет спрогнозировать доход этой компании в следующем квартале. Имеющиеся данные и диаграмма, построенная на их основе, находятся в рабочей книге Startup.xls (рис. 9). Видно, что данные имеют явный тренд (почти монотонно возрастают). Светлана хочет применить метод Хольта, чтобы спрогнозировать значение прибыли на одну акцию на тринадцатый квартал. Для этого необходимо задать начальные значения для L и Т Есть несколько вариантов выбора: 1) L равно значению прибыли на одну акцию за первый квартал и T = 0; 2) L равно среднему значению прибыли на одну акцию за 12 кварталов и T равно среднему изменению за все 12 кварталов. Существуют и другие варианты начальных значений для L и Т, но Светлана выбрала первый вариант.

Она решила воспользоваться средством Поиск решения, чтобы найти оптимальное значение параметров α и β, при которых значение среднего абсолютных ошибок в процентах было бы минимально. Для этого нужно выполнить такие действия.

Выбрать команду Сервис -> Поиск решения.

В открывшемся диалоговом окне Поиск решения задать ячейку F18 целевой и указать, что ее значение следует минимизировать.

В поле Изменяя ячейки ввести диапазон ячеек В1:В2. Добавить ограничения В1:В2 > 0 и В1:В2 < 1.

Кликнуть на кнопке Выполнить.

Полученный прогноз показан на рис. 10.

Как видно, оптимальными оказались значения α = 0,59 и β = 0,42, при этом среднее абсолютных ошибок в процентах равно 38%.

Рис. 9

Рис. 10

Учет сезонных изменений

При прогнозировании на основе данных временного ряда следует учитывать сезонные изменения Сезонные изменения — это колебания вверх и вниз с постоянным периодом в значениях переменной.

Например, если посмотреть на объемы продаж мороженого по месяцам, то можно увидеть в теплые месяцы (с июня по август в северном полушарии) более высокий уровень продаж, чем зимой, и так каждый год. Здесь сезонные колебания имеют период в 12 месяцев. Если используются данные, собранные по неделям, то структура сезонных колебаний будет повторяться через каждые 52 недели Другой пример анализируются еженедельные отчеты о количестве постояльцев, которые оставались на ночь в отеле, расположенном в бизнес-центре города Предположительно можно сказать, что большое число клиентов ожидается в ночи на вторник, среду и четверг, меньше всего клиентов будет в ночи на субботу и воскресенье, и среднее число постояльцев ожидается в ночи на пятницу и понедельник. Такая структура данных, отображающая количество клиентов в разные дни недели, будет повторяться через каждые семь дней.

Процедура, которая позволяет сделать прогноз с учетом сезонных изменений, состоит из таких четырех этапов

1) На основе исходных данных определяется структура сезонных колебаний и период этих колебаний.

2) Используя численный метод, описанный далее, из исходных данных исключают сезонную составляющую.

3) На основе данных, из которых исключена сезонная составляющая, делается наилучший возможный прогноз.

4) К полученному прогнозу добавляется сезонная составляющая.

Проиллюстрируем этот подход на данных об объемах сбыта угля (измеряемого в тысячах тонн) в США на протяжении девяти лет Фрэнк работает менеджером в компании Gillette Coal Mine, ему необходимо спрогнозировать спрос на уголь на ближайшие два квартала. Он ввел данные по всей угольной отрасли в рабочую книгу Уголь.xls и построил по этим данным график (рис. 11). На графике видно, что объемы продаж выше среднего уровня в первом и четвертом кварталах (зимнее время года) и ниже среднего во втором и третьем кварталах (весенне-летние месяцы).

Рис. 11

Исключение сезонной составляющей

Сначала необходимо вычислить среднее значение всех отклонений за один период сезонных изменений. Чтобы исключить сезонную составляющую в пределах одного года, используются данные за четыре периода (квартала). А чтобы исключить сезонную составляющую из всего временного ряда, вычисляется последовательность скользящих средних по T узлам, где T — продолжительность сезонных колебаний Для выполнения необходимых вычислений Фрэнк использовал столбцы С и D, как показано на рис. ниже. Столбец С содержит значения скользящего среднего по 4 узлам на основе данных, которые находятся в столбце В.

Теперь надо назначить полученные значения скользящего среднего средним точкам последовательности данных, на основе которых эти значения были вычислены. Эта операция называется центрированием значений. Если T нечетное, то первое значение скользящего среднего (среднее значений от первой до T-й точки) надо присвоить (T + 1)/2 точке (например, если T = 7, то первое скользящее среднее будет назначено четвертой точке). Аналогично среднее значений от второй до (T + 1)-й точки центрируется в (T + 3)/2 точке и т. д. Центр n-го интервала находится в точке (T+(2n-1))/2.

Рис. 12

Если T четное, как в рассматриваемом случае, то задача несколько усложняется, поскольку здесь центральные (средние) точки расположены между точками, по которым вычислялось значение скользящего среднего. Поэтому центрированное значение для третьей точки вычисляется как среднее первого и второго значений скользящего среднего. Например, первое число в столбце D отцентрированных средних на рис. 12, слева равняется (1613 + 1594)/2 = 1603. На рис. 13 показаны графики исходных данных и отцентрированных средних.

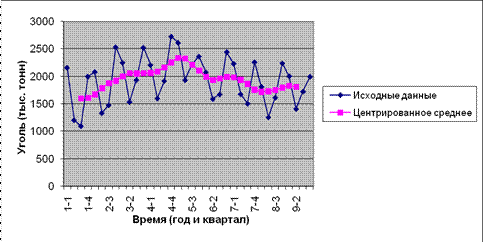
Рис. 13

Далее находим отношения значений точек данных к соответствующим значениям отцентрированных средних. Поскольку точкам в начале и конце последовательности данных нет соответствующих отцентрированных средних (см. первые и последние значения в столбце D), такое действие на эти точки не распространяется. Эти отношения показывают степень отклонения значений данных относительно типового уровня, определяемого отцентрированными средними. Заметим, что значения отношений для третьих кварталов меньше 1, а для четвертых — больше 1.

Рис. 14

Эти отношения являются основой для создания сезонных индексов. Для их вычисления группируются вычисленные отношения по кварталам, как показано на рис. 15 в столбцах G—О.

Рис. 15

Затем находятся средние значения отношений по каждому кварталу (столбец Е на рис. 15). Например, среднее всех отношений для первого квартала равно 1,108. Это значение является сезонным индексом первого квартала, на основе которого можно сделать вывод, что объем сбыта угля за первый квартал составляет в среднем около 110,8% относительного среднего годового объема сбыта.

Сезонный индекс — это среднее отношение данных, относящихся к одному сезону (в данном случае сезоном является квартал), ко всем данным. Если сезонный индекс больше 1, значит, показатели этого сезона выше средних показателей за год, аналогично, если сезонный индекс ниже 1, то показатели сезона ниже средних показателей за год.

Наконец, чтобы исключить из исходных данных сезонную составляющую, следует поделить значения исходных данных на соответствующий сезонный индекс. Результаты этой операции приведены в столбцах F и G (рис. 16). График данных, которые уже не содержат сезонной составляющей, представлен на рис. 17.

Рис. 16

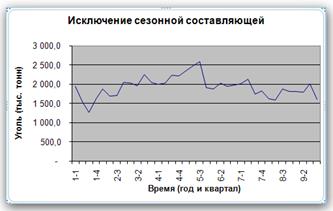
Рис. 17

Прогнозирование

На основе данных, из которых исключена сезонная составляющая, строится прогноз. Для этого используется соответствующий метод, который учитывает характер поведения данных (например, данные имеют тренд или относительно постоянны). В этом примере прогноз строится с помощью простого экспоненциального сглаживания. Оптимальное значение параметра α находится с помощью средства Поиск решения. График прогноза и реальных данных с исключенной сезонной составляющей приведены на рис. 18.

Рис. 18

Учет сезонной структуры

Теперь нужно учесть в полученном прогнозе (1726,5) сезонную составляющую. Для этого следует умножить 1726 на сезонный индекс первого квартала 1,108, в результате чего получим значение 1912 Аналогичная операция (умножение 1726 на сезонный индекс 0,784) даст прогноз на второй квартал, равный 1353. Результат добавления сезонной структуры к полученному прогнозу показан на рис. 19.

Рис. 19

Варианты заданий:

 

Задача 1

Дан временной ряд

t
x

1. Постройте график зависимости x = x(t).

1. Используя простое скользящее среднее по 4 узлам, спрогнозируйте спрос в 11-й момент времени.
2. Найдите среднее абсолютных отклонений.
3. Подходит ли такой метод прогнозирования для этих данных или нет? Почему?
4. Является ли данное приближение более предпочтительным по отношению к простому скользящему среднему по 3 узлам? Почему?
5. Подберите линейную функцию приближения данных методом наименьших квадратов.
6. Воспользуйтесь для прогноза методом экспоненциального сглаживания. Какой их использованных методов дает лучший рещультат?

 

Задача 2

Пользуясь моделью прогнозов доходов компании Startup Airlines (Startup.xls) выполните:

1. Подберите линейную функцию приближения данных методом наименьших квадратов.
2. Постройте прогноз значений прибыли с помощью взвешенного скользящего среднего по 4 узлам. Подберите оптимальные значения весов узлов с помощью средства Поиск решения.
3. Постройте прогноз значений прибыли с помощью метода экспоненциального сглаживания. Определите с помощью средства Поиск решения оптимальное значение .
4. Сравните точность построенных прогнозов с прогнозом, полученным по методу Хольта. Какой из методов дает более точные результаты?

 

Задача 3

Для временного ряда

t
x

выполните:

1. Используя взвешенное скользящее среднее по 4 узлам, и назначив веса 4/10, 3/10, 2/10, 1/10, спрогнозируйте спрос в 11-й момент времени. Больший вес следует назначать более поздним наблюдениям.
2. Является ли данное приближение более предпочтительным по отношению к простому скользящему среднему по 4 узлам? Почему?
3. Найдите среднее абсолютных отклонений.
4. С помощью средства Поиск решения найдите оптимальные веса узлов. Насколько уменьшилась ошибка приближения?
5. Воспользуйтесь для прогноза методом экспоненциального сглаживания. Какой их использованных методов дает лучший рещультат?

 

Задача 4

Проанализируйте временной ряд

Время

Спрос

1. Воспользуйтесь методом взвешенного скользящего среднего по 4 узлам, назначив веса 4/10, 3/10, 2/10, 1/10, чтобы получить прогноз в моменты времени 5—13. Больший вес следует назначать более поздним наблюдениям.
2. Найдите среднее абсолютных отклонений.
3. Считаете ли вы, что данное приближение более предпочтительно по сравнению с моделью простого скользящего среднего по 4 узлам? Почему?
4. С помощью средства Поиск решения найдите оптимальные веса узлов. На сколько удалось уменьшить значение ошибки?
5. Воспользуйтесь для прогноза методом экспоненциального сглаживания. Какой их использованных методов дает лучший результат?

 

Задача 5

Дан временной ряд

t
x

На основе данных этого ряда выполните следующее:

1. Пусть и 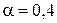. Спрогнозируйте спрос в 11-й момент времени методом экспоненциального сглаживания.
2. Если бы вы использовали метод экспоненциального сглаживания для прогнозов этого временного ряда, вы бы предпочли большее () или меньшее значение параметра ? Почему?
3. Путем минимизации среднего абсолютных ошибок в процентах определите с помощью средства Поиск решения оптимальное значение . Насколько изменилось при этом СООП?
4. Выполните аналогичный прогноз методом простого скользящего среднего с 3 узлами. Какой из полученных прогнозов кажется вам наилучшим? Почему?

 

Задача 6

Проанализируйте временной ряд

Время

Спрос

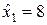1. Пусть и . Используйте метод экспоненциального сглаживания для прогноза спроса в периоды 2—13.
2. Найдите значение СООП для этого прогноза.
3. Повторите п.1 и 2, используя значение .
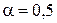4. Если бы вы использовали метод экспоненциального сглаживания для прогнозов этого временного ряда, какое значение параметра вы бы выбрали? Почему?
5. Чему равно оптимальное значение ? На сколько при этом меньше СООП по сравнению с п. 1.?
6. Выполните аналогичный прогноз методом простого скользящего среднего с 4 узлами. Сравните результаты с теми, что были получены в п. 1 Какой из полученных прогнозов кажется вам наилучшим? Почему?

 

Задача 7

Менеджер по маркетингу небольшой развивающейся компании, содержащей сеть продовольственных магазинов, обладает информацией об объемах продаж за все время существования самого прибыльного магазина (см. табл.).

Используя простое скользящее среднее по 3 узлам, спрогнозируйте значения в узлах с 4 до 11.

Используя взвешенное скользящее среднее по 3 узлам, спрогнозируйте значения в узлах с 4 до 11. Для определения оптимальных весов воспользуйтесь средством Поиск решения.

Методом экспоненциального сглаживания спрогнозируйте значения в узлах 2—11. Определите оптимальное значение параметра α с помощью средства Поиск решения.

Какой из полученных прогнозов наиболее точный и почему?

Период	Объем продаж, тыс. долл.

 

Задача 8

Дан временной ряд

t
x

1. Используя метод экспоненциального сглаживания, спрогнозируйте значения спроса в моменты 2–11.

2. Используя метод Хольта со значением , спрогнозируйте значения спроса в моменты 2–11.

3. Используя среднее абсолютных ошибок, определите, какой из двух методов дает более точный прогноз.

 

Задача 9

Рассмотрите следующую последовательность данных.

Время

Спрос

1. Постройте график этого временного ряда. Соедините точки отрезками прямых.
2. Используя простое скользящее среднее по 4 узлам, спрогнозируйте спрос для узлов 5–13.
3. Найдите среднее абсолютных отклонений.
4. Целесообразно ли использовать данный метод прогнозирования для представленных данных?
5. Является ли данное приближение более предпочтительным по отношению к простому скользящему среднему по 3 узлам? Почему?
6. Постройте по данным линейный и квадратичный тренд.
7. Воспользуйтесь для прогноза методом экспоненциального сглаживания. Какой их использованных методов дает лучший рещультат?

 

Задача 10

В рабочей книге Business_Week.xls приведены данные из журнала Business Week по ежемесячным объемам продаж автомобилей за 43 месяца.

1. Исключите из этих данных сезонную составляющую.
2. Определите наилучший метод прогнозирования для имеющихся данных.
3. Чему равен прогноз для 44-го периода?

 

Задача 11

В рабочей книге Банк.xls приведены показатели работы банка. Рассмотрите следующие методы прогнозирования значений этого временного ряда.

1. Простая схема прогнозирования, когда значение за прошлую неделю принимается за прогноз на следующую неделю.
2. Метод скользящего среднего (с числом узлов на ваше усмотрение). Попробуйте использовать несколько различных значений узлов.
3. Метод экспоненциального сглаживания. Подберите оптимальное значение параметра α с помощью средства Поиск решения.

Какой из предложенных выше методов прогнозирования вы бы порекомендовали для прогноза значений данного временного ряда?

 

Задача 12

В рабочей книге Банк.xls приведены показатели работы банка. Рассмотрите следующие методы прогнозирования значений этого временного ряда.

В качестве прогноза используется среднее значение показателя за все предыдущие недели.

Метод взвешенного скользящего среднего (с числом узлов на ваше усмотрение). Попробуйте использовать несколько различных значений узлов. Для определения оптимальных весов воспользуйтесь средством Поиск решения.

Метод экспоненциального сглаживания. Подберите оптимальное значение параметра α с помощью средства Поиск решения.

Какой из предложенных выше методов прогнозирования вы бы порекомендовали для прогноза значений данного временного ряда?

 

Литература

1. Шикин Е.В., Чхартишвили А.Г. Математические методы и модели в управлении. — М.: Дело, 2000. — 431 с.
2. Мур Дж., Уэдерфорд Л. и др. Экономическое моделирование в MS Excel. — М.: Вильямс, 2004. — 1024 с.