Метод скользящего среднего

Лабораторная работа № 7

Тема: Методы анализа временных рядов

Цель: Приобрести навыки прогнозирования значений временного ряда, в частности, выделения тренда и учета сезонной составляющей, а также навыки использования средств Пакет Анализа и Поиск решения, входящих в MS Excel.

Порядок выполнения работы:

1) Прогнозирование значений временного ряда.

1. Изучить теорию.

2. Построить график значений временного ряда.

3. Ответить на вопросы задачи.

4. Построить графики прогнозируемых значений (для каждого из полученных прогнозов).

2) Составление отчёта по лабораторной работе, в котором представляется:

· формулировка индивидуального задания;

· ответы на вопросы задачи;

· при необходимости, снимки экрана монитора, содержащие основные моменты решения задачи;

· графики значений временного ряда и прогноза.

 

Теория:

 

Временным рядом называется последовательность значений некоторого показателя во времени (например, объемов продаж, как на рис. 1).

Рис. 1

Анализ временных рядов (АВР) является способом выявления тенденций прошлого и продления их в будущее. Методы АВР осуществляют прогноз путем экстраполяции значений отдельной переменной на основе статистических данных за прошлый временной период. Основное допущение, которое при этом делается, заключается в том, что происшедшее в прошлом дает хорошее приближение в оценке будущего.

Развитие процессов, реально наблюдаемых в жизни, складывается из некоторой устойчивой тенденции (тренда) и некоторой случайной составляющей, выражающейся в колебании значений показателя вокруг тренда. На рис. 2 показано, как могут зависеть объемы продаж одного и того же товара на двух стадиях его жизненного цикла (в начале и в конце продаж).

Рис. 2

Кривые тренда сглаживают временной ряд значений показателя, выделяя общую тенденцию. Именно выбор кривой тренда во многом определяет результаты прогнозирования.

В большинстве случаев временной ряд, кроме тренда и случайных отклонений от него, характеризуется еще сезонной составляющей. Сезонная составляющая — это периодические изменения показателя. Обычная продолжительность сезонной составляющей измеряется днями, неделями или месяцами.

Рассмотрим несколько примеров использования метода экстраполяции. Предположим, что в журнале Wall Street Journal приведена сводка за последние 12 дней (включая сегодняшний) цен на апельсины, сложившихся на момент закрытия биржи. Используя эти данные, нужно предсказать завтрашнюю цену на какао (также на момент закрытия биржи). Рассмотрим несколько способов сделать это.

1. Если все имеющиеся значения цен существенны и имеют равную ценность для прогноза, можно найти среднее всех 12 значений, и это будет наилучший прогноз на завтра.
2. Если последнее (сегодняшнее) значение наиболее значимо по сравнению с остальными, то оно является наилучшим прогнозом на завтра.
3. Возможно, из-за быстрого изменения цен на бирже первые шесть значений уже устарели и не актуальны, в то время как последние шесть значимы и имеют равную ценность для прогноза Тогда в качестве прогноза на завтра можно взять среднее последних шести значений.
4. Если все значения существенны, но сегодняшнее 12-е значение наиболее значимо, а предыдущие 11-е, 10-е, 9-е и т.д. имеют все меньшую и меньшую значимость, следует найти взвешенное среднее всех 12 значений. Причем весовые коэффициенты для последних значений должны быть больше, чем для предыдущих, и сумма всех весовых коэффициентов должна равняться 1.
5. Можно на основе имеющихся 12 значений построить точечный график, а затем максимально близко к этим значениям провести линию регрессии. Значение на этой линии можно использовать для прогноза на завтра.

Первые два способа достаточно очевидны. Рассмотрим подробнее способы с третьего по пятый.

Подбор кривой

Начнем с пятого способа. Для подбора кривой (рис. 1) обычно используется метод наименьших квадратов, состоящий из двух этапов

1. Задается вид функции (линейная функция, квадратичная или какая-либо другая).
2. Среди функций выбранного вида нужно выбрать функцию, для которой сумма квадратов разностей между точками данных и значениями функции была бы минимальна.

В качестве примера, воспользуемся данными объемов продаж из файла Продажи.xls (рис. 3).

Рис. 3

Построим точечную диаграмму, отображающие реальные объемы продаж. Чтобы теперь построить по этим данным методом наименьших квадратов линейную функцию, прогнозирующие объемы продаж в будущем, надо выполнить такие действия.

1. Кликните на любой точке данных на диаграмме, все точки будут выделены.
2. Кликните правой кнопкой, и в появившемся меню выберите Добавить линию тренда
3. В открывшемся диалоговом окне Линия тренда по умолчанию будет выбран линейный тип функции.
4. Кликнете на кнопке ОК.

После этого на графике появится прямая линия тренда (рис. 4).

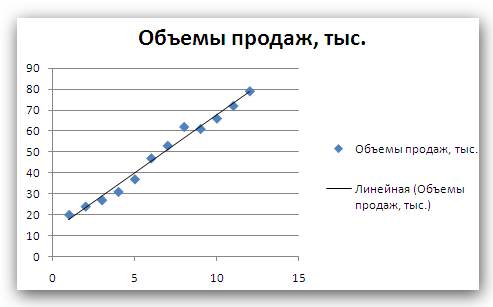
Рис. 4

Для того чтобы осуществить прогноз, нужно в диалоговом окне Линия тренда отметить интересующий интервал времени в пункте вперед на (или назад на).

В меню Линия тренда можно также задать параметры подбираемой кривой. Например, он можент быть экспоненциальной или полиномом заданной степени.

Следует отметить, что при подборе кривой неявно делается предположение, что все данные одинаково значимы (имеют равный вес). Этот метод позволяет получать стабильный прогноз, который мало чувствителен к изменению данных.

В нашем случае кривая тренда является прямой линий с уравнением 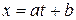. Коэффициенты и для этой кривой можно найти с помощью средства Пакет Анализа, выбрав средство Регрессия ( — Y-Пересечение, — Переменная X 1).

Метод скользящего среднего

Одним из предположений, лежащих в основе данного метода, является то, что более точный прогноз на будущее можно получить, если использовались недавние наблюдения, причем, чем «новее» данные, тем их вес для прогноза должен быть больше. Удивительно, но такой «наивный» подход оказывается чрезвычайно полезным для практики. Например, многие авиакомпании используют частный тип скользящего среднего для создания прогнозов спроса на авиаперелеты, которые, в свою очередь, используются в сложных механизмах управления и оптимизации доходов. Более того, практически все программные пакеты управления запасами содержат модули, выполняющие прогнозы на основе того или иного типа скользящего среднего.

Рассмотрим практический пример (Станки.xls). Менеджеру Виктор нужно спрогнозировать спрос на производимые его компанией станки. Необходимость в прогнозе вызвана создаваемой им моделью управления запасами (см. лаб. № 5), исходными данными для которой являются объемы продаж.

Простое скользящее среднее

Из группы методов скользящего среднего самым простым является метод скользящего среднего по N узлам. В этом методе среднее фиксированного числа N последних наблюдений используется для оценки следующего значения временно ряда. Например, используя данные о продажах станков opf первые три месяца года, Виктор получает для апреля значение

.

В общем случае расчетная формула выглядит так

.

Виктор вычислял объем продаж на основе простого скользящего среднего за 3 и 4 месяцев. Но какое количество узлов дает более точный прогноз. Для оценки точности прогнозов используются среднее абсолютных отклонений (САО) и среднее относительных ошибок, в процентах (СООП), вычисляемые по формулам

,

,

где N — количество прогнозов.

Согласно результатам, полученным на листе «Простое ск. среднее» рабочей книги Станки.xls (рис. 5), скользящее среднее за три месяца имеет значение САО равное 12,67 (ячейка D16), тогда как для скользящего среднего за 4 месяца значение САО равно 15,59 (ячейка F16). Это значит, что использование большего количества статистических данных скорее ухудшает, чем улучшает точность прогноза методом скользящего среднего.

Рис. 5

На графике (рис. 6), построенном по результатам наблюдений и прогнозов с интервалом 3 месяца, можно заметить ряд особенностей, общих для всех применений метода скользящего среднего.

Рис. 6

Значение прогноза, полученное методом простого скользящего среднего, всегда меньше фактического значения, если исходные данные монотонно возрастают, и больше фактического значения, если исходные данные монотонно убывают. Поэтому, если данные монотонно возрастают или убывают, то с помощью простого скользящего среднего нельзя получить точных прогнозов. Этот метод лучше всего подходит для данных с небольшими случайными отклонениями от некоторого постоянного или медленно меняющегося значения.

Основной недостаток метода простого скользящего среднего возникает в результате того, что при вычислении прогнозируемого значения самое последнее наблюдение имеет такой же вес (т.е. значимость), как и предыдущие. Это происходит потому, что вес всех N последних наблюдений, участвующих в вычислении скользящего среднего, равен 1/ N. Присвоение равного веса противоречит интуитивному представлению о том, что во многих случаях последние данные могут больше сказать о том, что произойдет в ближайшем будущем, чем предыдущие.

Взвешенное скользящее среднее

Вклад различных моментов времени можно учесть, вводя вес для каждого значения показателя в скользящем интервале. В результате приходим к методу взвешенного скользящего среднего, который математически можно записать так

,

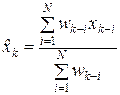где — вес, с которым используется показатель при расчете.

Вес — это всегда положительное число. В случае, когда все веса одинаковы, мы возвращаемся к простому скользящему среднему.

Теперь Виктор может использовать метод взвешенного скользящего среднего за 3 месяца. Но как ему выбрать веса? Конечно, это всегда можно сделать «методом проб и ошибок», выбирая веса произвольно, и оценивая точность прогноза при помощи САО (САО меньше, точность прогноза выше). Однако, пробы и ошибки могут продолжаться довольно долго. Есть более простой путь.

Используя средство Поиск решения, можно определить оптимальный вес узлов. Чтобы определить вес узлов с помощью средства Поиск решения, при котором значение среднего абсолютных отклонений было бы минимально, выполните такие действия

1. Выберите команду Сервис -> Поиск решения.
2. В открывшемся диалоговом окне Поиск решения установите ячейку G16 целевой (см. лист «Веса») и укажите, что ее значение должно быть минимальным.
3. В поле Изменяя ячейки введите диапазон В1:В3.
4. Введите ограничения В4 = 1,0, В1:ВЗ > 0, В1:В3 < 1, Bl < В2 и В2 < В3.
5. Щелкнув на кнопке Выполнить, получите результат, показанный на рис. 7.

Рис. 7

Полученные результаты показывают, что оптимальное распределение весов таково, что весь вес сосредоточен на самом последнем наблюдении, при этом значение среднего абсолютных отклонений равно 7,56. Этот результат подтверждает предположение о том, что более поздние наблюдения должны иметь больший вес.

Несмотря на то что в методе взвешенного скользящего среднего более поздним наблюдениям назначается больший вес, этот метод не решает практическую проблему, связанную с хранением данных, поскольку для вычисления одного значения прогноза все равно необходимо хранить все значения временного ряда. Рассмотрим метод экспоненциального сглаживания, который решает эту проблему.