Визначення коефіцієнта тертя кочення та ковзання за допомогою похилого маятника
Мета роботи. Вивчити причини виникнення тертя кочення. Визначити коефіцієнт тертя кочення.
Прилади та матеріали: установка ФМ-16, штангенциркуль.
Короткі теоретичні відомості.
При коченні циліндра по поверхні виникають сили тертя. Якщо циліндр котиться без ковзання, то створюється сила тертя спокою. Величина цієї сили визначається законом Кулона
F ≤ kN, (1)
де k – коефіцієнт тертя спокою,
N – сила нормального тиску.
Сила тертя завжди паралельна стичній поверхні тіл. Якщо циліндр котиться із проковзуванням, то появляється сила тертя ковзання, величина якої визначається рівністю.
F 1 = k 1 N, (2)
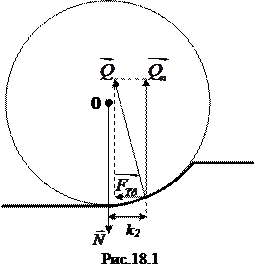Коефіцієнт тертя k1 залежить не тільки від властивостей поверхонь, що труться, але і від відносної швидкості.
При малих швидкостях його вважають постійним і рівним k 1 ≈ k.
При коченні циліндра по площині необхідно враховувати непружну деформацію площини і циліндра. Сила реакції опори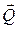 
не проходить через центр ваги циліндра, а трохи вперед по напрямку руху. Горизонтальна складова являє собою силу тертя кочення F тр. Момент сили тертя кочення відносно т.О рівний добутку нормальної складової сили реакції Q n на зміщення k2 (рис. 18.1).
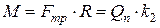, (3)
де k 2 – плече дії сили,
R – радіус циліндра
З рівняння (3)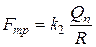 
Нормальну складову сили реакції Qn можна вважати рівною вазі циліндра.
Qn ≈ N
Тоді
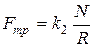(4),
Величину k 2 називають коефіцієнтом тертя кочення. Він суттєво відрізняється від коефіцієнтів k і k 1, оскільки є розмірною величиною і, по суті, характеризує плече сили тиску опори відносно осі циліндра.
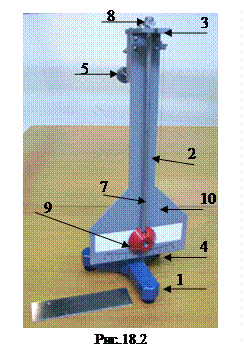
Маятник похилий зображено на рис. 18.2 і включає в себе: основу 1; стійку 2, у верхній частині якої встановлюється верхній кронштейн 3 з платформою 4; маятник кочення встановлюється на верхньому кронштейні 3 почергово.
Маятник ковзання представляє собою металічний стержень 7, з призматичною опорою 8 та обоймою 9, в яку вставляються змінні зразки у вигляді зрізаної кулі.
Маятник кочення являє собою металічну кулю, яка підвішена на капроновій нитці 10. Кулі є змінними і виготовлені із алюмінію, латуні і сталі. Кут нахилу маятника відраховують по шкалі. Тертя кочення виникає при коченні кульки по поверхні твердого пластичного тіла. Виникнення тертя кочення можна пояснити деформаціями кульки і площини. Визначення коефіцієнта тертя кочення ґрунтується на вимірюванні величини амплітуди коливань маятника, яка зменшується в результаті роботи сил тертя кочення.
Знайдемо вираз для визначення коефіцієнта тертя кочення. За n коливань при переході маятника з т. В в точку В΄ маятник втрачає енергію Δ Ер = mg Δ h, яка рівна роботі сил опору на пройденому кулькою шляху S.
Δ Ер = Δ А,
 |
де Δ А – робота сил тертя кочення.
Враховуючи, що Δ А = Fтр · S, отримаємо
mg Δ h = Fтр S
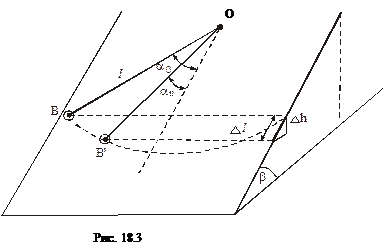
З рисунка 18.3 видно, що Δ h = Δ l sin β. Тоді з врахуванням рівності (4) і того, що N = mg cos β, отримаємо
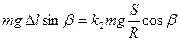(5)
де R – радіус кульки, β – кут нахилу маятника.
Відстань
Δ l = l (cosαn – cosα0), (6)
де α0 – амплітудне значення кута відхилення маятника в початковий момент часу, αn – амплітудне значення кута через n коливань, l – довжина маятника.
Відстань яку пройде кулька за n коливань знаходиться за формулою:
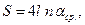(7)
де 
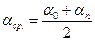(8)
При малих значеннях α0 і αn
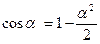. (9)
З формули (5) коефіцієнт тертя k 2 відповідно рівний:
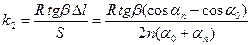
Врахувавши формулу (9) отримаємо вираз для знаходження коефіцієнта тертя кочення.
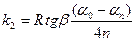(10).
З (10) видно, що для визначення коефіцієнта тертя кочення необхідно виміряти діаметр кульки, кути відхилення нитки (відповідно, початковий та кінцевий), число повних коливань кульки та величину кута нахилу нитки до горизонту.
Порядок виконання роботи.
Дослід 1. Визначення коефіцієнта тертя кочення.
1. Виміряти радіус кульки.
2. Нахилити площину маятника на кут β ≈ 3°.
3. Відхилити кульку від положення рівноваги на кут α0 = 5° і відпустити.
4. Визначити величину кута αn після п’яти повних коливань. Дослід повторити три рази при одному і тому ж значенні α0, обчисливши при цьому середнє значення αср..
5. Виміряні величини занести в таблицю і за формулою (10) обчислити середнє значення коефіцієнта тертя кочення.
6. Пункти 3°÷ 5° повторити для β = 6° і β = 10°.
7. Оцінити похибку вимірювання коефіцієнта тертя кочення.
Табл. 1.
| R, м | Δ R, м | β, рад | Δ β, рад | α 0, рад | Δ α 0, рад | α n, рад | Δ α n, рад | n | k 2, м | |
| сер. |
Дослід 2. Визначення коефіцієнта тертя ковзання.
1. Скласти установку "Маятник похилий" (див. рис. 16.2).
2. Встановити кут нахилу платформи рівним 0°.
3. Використовуючи маятник кочення в якості вертикального орієнтира, за допомогою регулювальних опор основи виставити стійку приладу в строго вертикальному положенні.
4. Протерти досліджувані поверхні змінних пластин, зрізаної кулі і кулі маятника кочення етиловим спиртом і витерти досуха.
5. Встановити стальну пластину на платформу 4.
6. Вставити зрізану стальну кулю в обойму 9 маятника ковзання сферичною поверхнею назовні.
7. Повісити маятник ковзання за допомогою призматичної опори на верхній кронштейн 3 так, щоб зрізана куля стикнулася зі встановленою на платформу пластиною і вісь маятника була паралельна лицьовій поверхні платформи.
8. При необхідності підрегулювати положення підстави так, щоб покажчик маятника опинився напроти нульової поділки шкали відліку кута відхилення маятника, але без порушення вертикального положення стійки.
9. Встановити кут нахилу платформи рівним 2°.
10. Відвести рукою маятник в одне з крайніх положень і записати початковий кут відхилення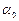 
за шкалою відліку кута відхилення маятника.
11. Відпустити маятник і записати кут відхилення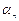 
при здійсненні маятником n повних коливань. Перевести значення кутів в радіаннy міру.
12. Виміряні величини занести в таблицю 2.
13. Визначити середнє значення коефіцієнта тертя ковзання за формулою: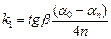 
, де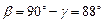 
. Формула справедлива при умові, що кут 
.
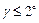14. Повторити пункти 5-13 для пластини із фторпласту.
15. Обчислити похибки вимірювання та зробити висновки.
Табл. 2.
| № п/п | Пластина | β, рад | Δ β, рад | α 0, рад | Δ α 0, рад | α n, рад | Δ α n, рад | n | k 1 |
| Стальна | |||||||||
| сер. | |||||||||
| Фторпластова | |||||||||
| сер. |
Контрольні питання.
1. Тертя. Тертя спокою. Тертя ковзання. Сила тертя.
2. Закон Амонтона – Кулона.
3. Тертя кочення. Методика визначення коефіцієнта тертя кочення та ковзання.
Література.
1. Матвеев А.Н. Механика и теория относительности. – М.: Высшая школа, 1986. – 320 с.
2. Физический практикум. Механика и молекулярная физика. Под ред. Ивероновой В.И. – М.: Наука, 1983. – 352 с.
3. Гольдин Л.Л. и др. Лабораторные занятия по физике. – М.: Наука, 1983. – 704 с.
4. Савельев И.В. Курс общей физики, т. 1. - М.: 1982. - 432 с.
5. Лабораторный практикум по физике /Под ред. А.С.Ахматова. - М.: 1980. - 360 с.
1. Физический практику. Механика и молекулярная физика / Под ред. Ивероновой В. И. – М.: Наука. 1967. – 352 с.
2. Гольдин Л. Л. и др. Лабораторные занятия по физике. – М.: Наука. 1983. – 704 с.
