21. Перечислите возможные виды однородностей уравнений высших порядков.
(Однородность относительно функцией  , однородность относительно всех переменных и дифференциалов:
, однородность относительно всех переменных и дифференциалов:  в обобщенном смысле.)
в обобщенном смысле.)
22. Как проверяется однородность относительно функцией  .
.
( .)
.)
23. Какая замена понижает порядок уравнения с такой однородностью.
(Такое уравнение допускает понижение порядка, если ввести новую функцию и (х), а  .)
.)
24. Запишите, применяя правило дифференцирования сложной функции, как выразятся производные у по х первого, второго и третьего порядка через новую функцию и.
(Выражая производные через новую функцию
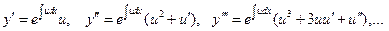
каждая производная определяется через выражение, имеющее производную на порядок ниже.)
25. Как используется однородность уравнения.
(Подставляя в уравнение найденные производные, получим, что все слагаемые умножаются на одну и ту же степень показательной функции 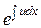 (в силу однородности уравнения). Разделив на этот множитель, получим уравнение (п - 1)-го порядка на функцию и (х).)
(в силу однородности уравнения). Разделив на этот множитель, получим уравнение (п - 1)-го порядка на функцию и (х).)
26. Как проверяется однородность относительно всех переменных и дифференциалов:  в обобщенном смысле.
в обобщенном смысле.
(Уравнение является однородным относительно своих переменных в обобщенном смысле, если оно не меняется при замене:
 ,
,  ,
,  ,
,  ,…,
,…,  ,
,
где т – некоторая постоянная.)
27. Как определяется т. Всегда ли это возможно.
(Число т определяется специальным образом, так, чтобы все одночлены равенства, полученного после замены указанной выше, имели равные показатели степеней параметра 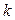 .
.
Такое значение т не всегда возможно найти, т.к. на одно число m составляется несколько равенств – их число зависит от количества слагаемых в уравнении. Составленная система переопределена, и ее решение не всегда существует.)
28. Какая замена используется для преобразования уравнения.
(После того как найдено т, необходимо выполнить замену переменных  , где
, где  - новая независимая переменная,
- новая независимая переменная,  - новая неизвестная функция.)
- новая неизвестная функция.)
29. Запишите, применяя правило дифференцирования, как выразятся дифференциалы  через новую переменную
через новую переменную  и функцию
и функцию  .
.
( )
)
30. Как влияет однородность уравнения на вид равенства, полученного после сделанной подстановки.
(После сокращения на показательную функцию, полученное уравнение не будет содержать переменной  в явном виде и, следовательно, оно сводится к типу III.)
в явном виде и, следовательно, оно сводится к типу III.)
Практические задания
Пример 1. Заменить в формуле  , п - кратное интегрирование однократным по параметру.
, п - кратное интегрирование однократным по параметру.
Решение: Пусть необходимо решить задачу Коши с начальными данными:  .
.
Начнем с двукратного интегрирования, т.е. с определения  , для большей ясности переобозначим переменные в этих интегралах так
, для большей ясности переобозначим переменные в этих интегралах так
 Рис. 1
Рис. 1
|
 .
.
Теперь, рассматривая правую часть как двойной интеграл в плоскости ХОУ (рис. 1) поменяем порядок интегрирования. Сначала интегрирование выполняется вдоль направления OХ от прямой x=z до прямой х, а второй интеграл вдоль направления ОZ от прямой  до z=x
до z=x
 .
.
Далее понизив порядок уравнения до n- 3, получим
 .
.
Интеграция выполняется на том же треугольнике плоскости XOZ, поэтому, изменив порядок интегрирования и пределы, находим
 .
.
Методом математической индукции можно доказать, что решение уравнения находится по формуле Коши:  .)
.)
Пример 2. Решить уравнение  .
.
Решение: Общее решение можно записать в виде:
 .
.
Выполнив интегрирование, найдем:
 .
.
После подстановки верхнего и нижнего пределов и приведения подобных, имеем
 ,
,
где  - играют роль постоянных интегрирования.
- играют роль постоянных интегрирования.
Пример 3. Проинтегрировать уравнение 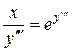 .
.
Решение: Уравнение не разрешимо относительно  , поэтому представим данное уравнение в параметрическом виде
, поэтому представим данное уравнение в параметрическом виде
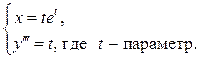
Используя  ,
,  , понизим порядок производной трижды, интегрируя получим
, понизим порядок производной трижды, интегрируя получим

Общее решение будет записано в параметрическом виде

Пример 4. Свести уравнение  к уравнению первого порядка и проинтегрировать.
к уравнению первого порядка и проинтегрировать.
Решение: Уравнение не содержит функции  , поэтому можно выполнить замену
, поэтому можно выполнить замену  , тогда
, тогда  , и исходное уравнение примет вид
, и исходное уравнение примет вид  . Разделяя переменные, получим
. Разделяя переменные, получим
 ,
,
 или
или  .
.
Возвращаясь к функции у получаем уравнение второго порядка типа I
 .
.
Выполняя понижение порядка дважды, найдем решение уравнения
 ,
,
 .
.
Пример 5. Найти общее решение уравнения  .
.
Решение: Уравнение не содержит переменной х в явном виде.
Введем новую функцию р (у) = у', тогда по формулам выполним замену второй производной  , и исходное уравнение примет вид:
, и исходное уравнение примет вид:
 .
.
Очевидно, что  является решением, тогда (так как р (у) = у')
является решением, тогда (так как р (у) = у')  и уравнению удовлетворяет тривиальное решение
и уравнению удовлетворяет тривиальное решение  Теперь положим
Теперь положим  Разделяя переменные и интегрируя каждую часть, имеем
Разделяя переменные и интегрируя каждую часть, имеем
 .
.
Возвращаясь к принятым обозначениям, получим
 ,
,
что позволяет найти общее решение уравнения в неявном виде
 .
.
Пример 6. Решить уравнение  ,
,  .
.
Решение: Выполнив замену 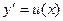 ,
,  получим уравнение первого порядка
получим уравнение первого порядка  , которое можно проинтегрировать
, которое можно проинтегрировать  , после замены:
, после замены: 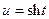 ,
,  , имеем
, имеем  .
.
Тогда получим  , следовательно
, следовательно  в результате находим искомую функцию
в результате находим искомую функцию  .
.
Пример 7. Проинтегрировать уравнение  ,
,  .
.
Решение: Выполним процедуру пункта V а):  ,
,  , что приводит к уравнению
, что приводит к уравнению  ,
,  , выделим полные производные
, выделим полные производные  и проведем понижение порядка
и проведем понижение порядка  или
или  . После разделения переменных выполним интегрирование
. После разделения переменных выполним интегрирование
 ,
,  .
.
Вернемся к первоначальной функции
 .
.
Сведем уравнение к параметрической системе

Из второго равенства найдем  :
:  и подставим в первое соотношение
и подставим в первое соотношение
 ,
,  ,
,
повторим процедуру еще раз
 ,
,  ,
,  .
.
Ответ: 
Пример 8. Определить тип уравнения  и решить.
и решить.
Решение: Уравнение представляет собой однородное уравнение по у, у', у'' и поэтому относится к случаю VI. Подстановка  и сокращение левой и правой части уравнения на
и сокращение левой и правой части уравнения на 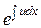 дает равенств
дает равенств
 , (1)
, (1)
представляющее частный случай уравнения Риккати
 . (2)
. (2)
Такое уравнение можно привести к линейному уравнению, если известно его какое-либо частное решение. Пусть у 1 - некоторое решение, тогда
 .
.
Введем новую искомую функцию z (х), такую, что
 . (3)
. (3)
Подставляя в (2) и принимая во внимание, что у 1 - решение уравнения, получим для функции z (х) линейное уравнение
 .
.
В исследуемом равенстве (1) таким частным решением может служить функция и 1 = 1/ х (это легко проверить непосредственной подстановкой в равенство (1)). Используя вид подстановки (3) находим уравнение для z (х)
 .
.
Интегрирование позволяет найти общий интеграл уравнения

или
 .
.
Пример 9. Найти общее решение уравнения
 .
.
Решение: Проверим однородность уравнения относительно всех переменных и дифференциалов, для этого распишем производные через дифференциалы
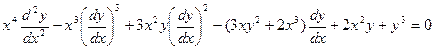 ,
,
и выполним подстановку
 ,
,
 .
.
Оказывается, каждый член имеет третий порядок относительно параметра t, следовательно, уравнение однородно относительно всех переменных и дифференциалов. Выполним замену переменных по формулам  ,
,  ,
,  :
:
 ,
,
после сокращения на  , раскрытия скобок и приведения подобных
, раскрытия скобок и приведения подобных
 .
.
Получаем уравнение второго порядка, не содержащее независимой переменной  и функции и, а, следовательно, можно разделить переменные и выполнить интегрирование
и функции и, а, следовательно, можно разделить переменные и выполнить интегрирование
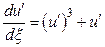 ,
,  ,
,
разложим методом неопределенных коэффициентов подынтегральную функцию на сумму двух слагаемых

выполним интегрирование

Выразим и':  и выполним интегрирование, используя параметрическую замену
и выполним интегрирование, используя параметрическую замену

Выполнив дифференцирование второго равенства системы, найдем 

и подставим в первое равенство системы
 или после интегрирования
или после интегрирования 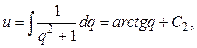
в результате получим параметрическую запись функции

Вернемся к переменным  ,
,  , и получим решение исходного уравнения записанное в параметрическом виде
, и получим решение исходного уравнения записанное в параметрическом виде

Пример 10. Решить уравнение

Решение: Проверим, является ли дифференциальное уравнение однородным в обобщенном смысле
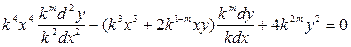 ,
,
т.е. должны выполняться равенства
 ,
,
это возможно если т = 2. Следовательно, в уравнении следует сделать замену  ,
,  :
:
 .
.
После сокращения на  и элементарных преобразований, запишем
и элементарных преобразований, запишем
 (4)
(4)
в этом уравнении отсутствует независимая переменная  , поэтому используя пункт III, проведем замену:
, поэтому используя пункт III, проведем замену:  - новая независимая переменная,
- новая независимая переменная,  - новая неизвестная функция,
- новая неизвестная функция,  , в результате уравнение (4) понижается на порядок
, в результате уравнение (4) понижается на порядок
 или
или  .
.
Имеем следующие решения:
1.  , тогда
, тогда  , возвращаясь к старым переменным
, возвращаясь к старым переменным  , тогда окончательно имеем решение
, тогда окончательно имеем решение 
2.  после разделения переменных
после разделения переменных  и интегрирования получим
и интегрирования получим  или
или 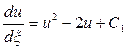 . Производя еще раз разделение переменных и интегрирование
. Производя еще раз разделение переменных и интегрирование
 ,
,

Переход к переменным у и х  дает следующее решение
дает следующее решение

Пример 11. Проинтегрировать уравнение, выделив полные производные
 .
.
Решение: Легко заметить, что если разделить все члены на выражение  , то каждое слагаемое будет представлять полную производную
, то каждое слагаемое будет представлять полную производную
 или
или  .
.
В результате интегрирования получим уравнение первого порядка
 или
или  .
.
Разрешая полученное равенство относительно производной, имеем
 ,
,  .
.
Полученное уравнение допускает разделение переменных и интегрирование
 ,
,  .
.






