Примеры нелинейных динамических систем
1.1.1. Система Ван дер Поля.
1.1.2. Исследование поведения системы.
1.1.3. Бифуркация рождения цикла.
1.1.4. Система Ван дер Поля с периодическим возмущением.
1.4. Система Лоренца.
1.4.1. Вид системы Лоренца
1.4.2. Исследование на неподвижные точки.
1.4.3. Численное исследование динамики системы Лоренца.
1.4.4. Странный аттрактор.
Нелинейная система с предельным циклом (система Ван дер Поля)


Динамика осциллятора Ван дер Поля при w2 = 2 и c = 1
Предельный цикл – устойчивый режим периодических колебаний в нелинейных системах после завершения переходных процессов
Демонстрация динамики
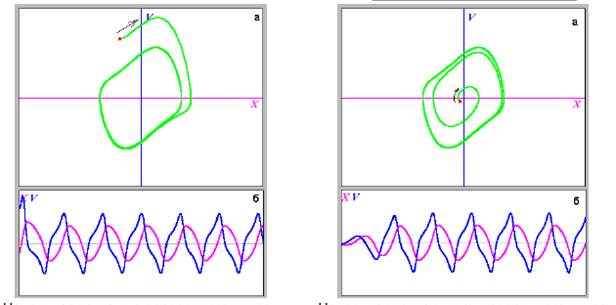
| Начальная точка вне предельного цикла. | Начальная точка внутри предельного цикла. |
Примеры решения системы ОДУ Ван-дер-Поля
Покажем применение решателя ОДУ ode15s на ставшем классическим примере – решении нелинейного дифференциального уравнения второго порядка (уравнения Ван-дер-Поля), записанного в виде системы из двух дифференциальных уравнений:
y'1 =y2;
y'2 = m*(1–y12)*y2–y1
при начальных условиях
y1(0)=0; y2(0)=1.
Это уравнение описывает колебания в нелинейной системе второго порядка, например в LC-генераторе на электронной лампе или полевом транзисторе, и является классическим примером математического моделирования этих устройств. Поведение системы Ван-дер-Поля существенно зависит от параметра m, который задает степень влияния нелинейности на возникновение и развитие колебаний. При больших m представленная система ОДУ является жесткой. Возьмем значение μ=100.
Перед решением нужно записать систему дифференциальных уравнений в виде ODE-функции. Для этого в главном меню выберем File ⇒ New ⇒ MMFile и введем
function dydt = vdp100(t,y)
dydt = zeros(2,1); dydt(1) = y(2);
dydt(2) = 100*(1 – y(1)^2)*y(2) – y(1);
Сохраним данный m-файл-функцию.
Тогда решение решателем ode15s и сопровождающий его график (рис. 8.5) можно получить, используя следующие команды:
>> [T,Y]=ode15s(@vdp100,[0 30],[2 0]); plot(T,Y)
>> hold on; gtext('y1'), gtext('y2')
Последние команды позволяют с помощью мыши нанести на графики решений y1 = y(1) и y2 = y(2) помечающие их надписи.

Рис. 8.5. Пример решения системы дифференциальных уравнений
численным методом
Рассмотрим еще один пример решения уравнения Ван-дер-Поля вида y''1 = 2*(1–y12)*y1–y'1 при m = 2. Оно сводится к следующей системе уравнений:
y'1 = y2,
y'2 = 2*(1–y12)*y1–y2.
Подготовим m-файл ode-функции vdp.m:
function [out1,out2,out3] = vdp(t,y,flag)
if nargin < 3 | isempty(flag)
out1 = [2.*y(2).*(1-y(2).^2)-y(1); y(1)];
else
switch(flag)
case 'init' % Return tspan, y0 and options
out1 = [0 20];out2 = [2; 0]; out3 = [ ];
otherwise
error(['Unknown request ''' flag '''.']);
end
end
Тогда решение системы с помощью решателя ode23 реализуется следующими командами:
>> [T,Y] = ode23(@vdp,[0 20],[2 0]);
>> plot(T,Y(:,1),'-',T,Y(:,2),'-.')
График решения для последнего примера показан на рис. 8.6. Нетрудно заметить, что в данном случае переходные процессы имеют затухающий характер и генерации периодических колебаний нет.

Рис. 8.6. Пример решения системы ОДУ
Бифуркация
Изменение параметра, который называется управляющим, вызывает потерю устойчивости одного состояния (или режима функционирования) системы и переход к другому, качественно отличному от прежнего, состоянию (режиму функционирования). Это явление называется бифуркацией (раздвоением), а значение параметра, при котором это происходит – точкой бифуркации. Графическое отображение зависимости характера поведения системы от параметра, носит название бифуркационной диаграммы.







