Экспоненциальное распределение. НСВ с функцией и плотностью распределения, определяемыми соотношениями:

НСВ с функцией и плотностью распределения, определяемыми соотношениями:

имеет экспоненциальное (потенциальное) распределение , где – параметр распределения ()

Среднее значение и дисперсия СВ равны: .

Экспоненциальное распределение можно рассматривать как частный случай распределений:

· гамма - распределения при ;

· Вейбулла-Гнеденко при с = 1.

Алгоритм моделирования СВ основан на методе обратной функции. Обратная функция для , определяемой (25), находится при решении уравнения относительно x: (26).

Далее в соответствии с методом обратной функции алгоритм моделирования СВ состоит из двух шагов:

· моделирование реализации a БСВ;

· вычисление в соответствии с (26) реализации x СВ , где учтено, что a и a-1 одинаково распределены.

Коэффициент использования БСВ к=1.

5. Распределение Лапласса

6. Распределение Вейбулла-Гнеденко

НСВ с плотностью распределения

имеет распределение Вейбулла-Гнеденко , которое имеет вид:

Среднее значение и дисперсия равны:

здесь Г(x)-гамма-функция Эйлера, то есть

Частными случаями распределения с плотностью (31) являются:

1) экспоненциальное распределение при с = 1;

2) распределение Релея, имеющее плотность

при с = 2 и

Алгоритм моделирования СВ основан на методе обратной функции и состоит из следующих шагов:

· моделирование реализации а БСВ;

· принятие решения о том, что реализацией СВ является величина x, вычисляемая с учетом (32) по формуле:

Коэффициент использования БСВ к=1.

Гамма-распределение

НСВ с плотностью распределения

имеет гамма-распределение с параметрами: - параметр формы; b>0 – параметр масштаба. Здесь Г( ν ) - гамма-функция Эйлера:

Среднее значение и дисперсия равны:

При гамма-распределение совпадает с экспоненциальным: .

Для произвольного целого гамма-распределение называется распределением Эрланга порядка с параметром .

Если – целое число, – независимые случайные величины, распределенные по стандартному экспоненциальному закону , то СВ вида: имеет распределение .

В соответствии с методом обратной функции: – независимые БСВ. С учётом этого из (33) следует:

Если – независимые БСВ, 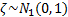, то СВ вида: имеет распределение .

В лабораторной работе полагалось, что – целое число. Для этого случая алгоритм моделирования описывается формулой (34). Коэффициент использования БСВ .

Распределение Коши

НСВ с плотностью распределения (38) имеет распределение Коши C(m, c) с параметрами: c>0 - параметр масштаба; 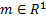- параметр положения (мода, медиана).

Функция распределения СВ имеет вид:

Известно, что если - независимые стандартные гаусовские величины, то СВ ξ вида имеет распределение Коши C(0,1).

Алгоритм моделирования СВ основывается на формуле (39) и состоит из двух шагов:

· моделирование независимых реализаций СВ ;

· принятие решения о том, что реализацией СВ является величина

Коэффициент использования БСВ k = 1.

Хи-квадрат распределение

НСВ с плотностью распределения

имеет хи-квадрат распределение с m степенями свободы (m>0 – натуральное число, параметр распределения). Здесь Г(z) – гамма-функция Эйлера.

Среднее значение и дисперсия равны: .

Известно, что, если - – независимые стандартные гаусовские СВ, то СВ (43) имеют плотность распределения (42).

В основе первого алгоритма моделирования СВ лежит свойство (43): в качестве реализации СВ принимается величина x, вычисленная по независимым реализациям СВ по формуле: .

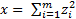Коэффициент использования БСВ , где – число реализаций БСВ, необходимых для моделирования одной реализации СВ .

Пусть – независимые реализации БСВ, z – независимая от реализация СВ . Второй алгоритм моделирования СВ предполагает, что в качестве реализации СВ принимается величина x, вычисляемая по формулам: .

Коэффициент использования БСВ для случаев (44), (45) соответственно равен: .

Распределение Фишера

НСВ с плотностью распределения

имеет распределение Фишера (F-распределение) с l и m числом степеней свободы (l,m –натуральные числа, параметры распределения).

Среднее значение и дисперсия ξ ~ равны: .

Пусть . Тогда . Алгоритм моделирования определяется этим соотношением.