Понятие непрерывной случайной величины
Непрерывной случайной величиной (НСВ) называется случайная величина 
, имеющая абсолютно-непрерывное распределение вероятностей, определяемое функцией распределения:
и плотностью распределения:
НСВ 
имеет следующие основные числовые характеристики:
• среднее значение:
• дисперсия:
На практике для описания НСВ используются модельные непрерывные законы распределения с функциональными характеристиками, заданными в параметрическом виде: 
Во многих практических задачах выборку наблюдений нельзя считать однородно, поскольку выборочные наблюдения соответствуют не одной, а нескольким моделям. Распределение такой выборки описывается смесью распределений. В связи с этим, актуальной задачей является задача моделирования смеси распределений.
Основными методами построения моделирующих алгоритмов для непрерывных законов распределения являются: метод обратной функции, метод исключения и метод функциональных преобразований.
В приложениях часто возникает задача моделирования НСВ в условиях априорно неопределенности, когда плотность неизвестна. В этих случаях может осуществляться моделирование СВ с заданной гистограммой или моделирование СВ с заданным полигоном частот. Гистограмма и полигон частот выступают как оценки плотности, построенные по имеющейся выборке экспериментальных данных.
Методы моделирования непрерывной случайной величины
Метод обратной функции
Метод обратной функции является одним из универсальных методов моделирования НСВ ξ с заданной плотностью 
и функцией распределения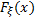 
.
Пусть 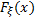– строго монотонная возрастающая функция. Найдем обратную функцию 
, решая относительно х следующее уравнение: 
. Известно, что если α – БСВ, то СВ ξ, определяемая выражением: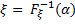 
, имеет заданную плотность (функцию распределения ).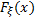
Таким образом, имеет место следующий алгоритм моделирования НСВ:
1) Моделируется реализация БСВ 
;
2) Принимается решение о том, что реализацией СВ является величина х, определяемая по формуле: 
;
3) Коэффициент использования БСВ k = 1.
На этом методе основываются алгоритмы моделирования НСВ с распределениями: равномерным, экспоненциальным, Лапласа, Вейбулла-Гнеденко, Коши, логистическим, гамма-распределением.
Метод исключения
В случаях, когда плотность распределения моделируемой НСВ имеет сложны аналитический ряд, нахождение функции распределения 
, а тем более обратной функции затруднительно, что делает невозможным применение метода обратной функции для моделирования СВ .
В этом случае может оказаться полезным другой универсальный метод моделирования, называемый методом исключения. Он заключается в следующем.
Обозначим: 
– область, ограниченную кривой 
и осью абсцисс. Определим мажорирующую функцию 
и область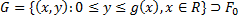 
. Заметим, что мажорирующая функция должна иметь значительно более простой аналитический вид, чем 
. Область G при этом также имеет простой вид (треугольный, прямоугольный), позволяющий легко моделировать случайный вектор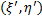 
, равномерно распределенный в области G (например, при помощи метода обратной функции).
Алгоритм моделирования, основанный на методе исключения, включает следующие этапы:
1) Подбор мажорирующей функции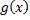 
;
2) Моделирование реализации 
случайного вектора 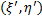с равномерным распределением в области G;
3) Принятие решения о том, что реализацией является 
при выполнении следующего условия: 
Запись 
означает, что точка с координатами 
принадлежит области 
. Точки 
, не попавшие в , исключаются из рассмотрения. Отсюда и происходит название метода.
Для моделирования случайного вектора 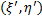с равномерным распределением в области G полагают:
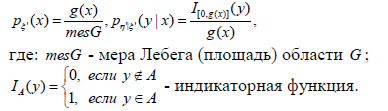
Моделирование СВ 
и 
(при условии, что 
) осуществляется по методу обратной функции.
Средний коэффициент использования БСВ 
, где l – количество БСВ (обычно l = 2), используемых для получения одной реализации (x, y) случайного вектора 
.
Данный метод используется для построения одного из алгоритмов гамма-распределения.
Алгоритмы моделирования для основных непрерывных распределений
Равномерное распределение
НСВ ξ имеет равномерное распределение на интервале [a, b), обозначаемое R(a, b), если функция и плотность распределения ξ определяются соотношениями:
Для произвольных значение параметров распределения a, b распределение R(a, b) обобщает распределение R(0, 1) БСВ α.
Среднее значение: 
, дисперсия: 
.
Алгоритм моделирования СВ ξ основан на методе обратной функции. Обратная функция для 
находится при решении уравнения 
относительно х: 
.
Далее в соответствии с указанным методом алгоритм моделирования реализации СВ включает два шага:
· моделирование реализации БСВ η
· принятие решения о том, что реализацией ξ является величина x: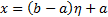 
Коэффициент использования БСВ k = 1.
